Методы расчета электронных энергетических состояний в твердых телах. Приближения свободных и сильносвязанных электронов.
Энергетическая диаграмма металлов.
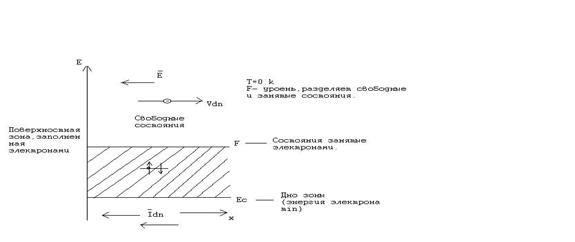
F- уровень Ферми – электроны имеют на уровне F –максимальную энергию при T=0° к (энергия Ферми).
Верхняя зона-зона проводимости.
При наложении электрического поля на M электроны беспрепятственно ускоряются и создают электронный электрический ток.
Скорость направленного движения е – скорость дрейфа – Vdn
ζ dn – плотность потока.
Энергетическая диаграмма диэлектриков и п/п.
К диэлектрикам и полупроводникам относят вещества , у которых верхняя заполненная электронами зона – валентная зона - полностью занята электронами.
Пример образования валентной зоны и зоны проводимости представлен на рис.3.
Рис.3. Образование энергетических зон из атомных уровней в алмазе, Ge и Si
 |
ΔEg – ширина запрещенной зоны (интервал по шкале энергии от уровня Ev до Ec зоны проводимости)
Зона проводимости - нижняя из не заполняемых зон электронами.
Диэлектрики и полупроводники отличаются лишь величиной ΔEg (ΔEg(д)> ΔEg(п/п))
При 0°К в отличие от металлов диэлектрики и полупроводники не проводят электрический ток.(изоляторы)
Для перевода диэлектриков(полупроводников) в проводящее состояние необходимо их нагреть и осветить светом с энергией фотона hν>ΔEg:
связанные электроны валентной зоны переходят в свободное состояние зоны проводимости.
В зоне проводимости – появляется электроны проводимости, а в валентной зоне – электронные вакансии – свободные уровни у потолка валентной зоны.
Почти заполненная валентная зона тоже вносит вклад в проводимость диэлектриков и полупроводников.
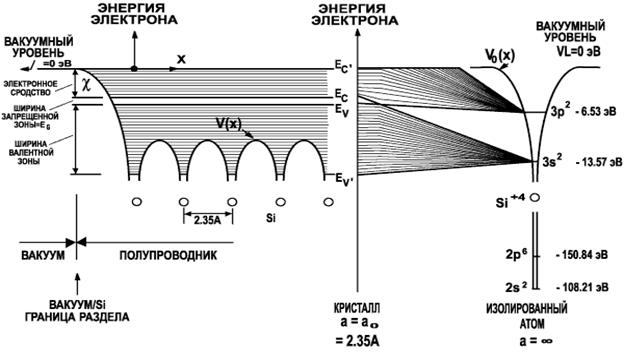
Рис. 4. Структура энергетических уровней в изолированном атоме кремния, а также схематическая структура энергетических зон, возникающих при сближении этих атомов и образовании монокристаллического кремния
Полуметаллы – класс веществ, промежуточных между металлами и полупроводниками (плохие металлы с маленькой концентрацией электронов)
Они образуются при наложении зоны проводимости на валентную зону.
проводимое условие- число занятых вакансий в ЗП равно числу состояний свободных
электронов в валентной зоне
Фотонные кристаллы – искусственные кристаллы (в природе их нет) с периодом (d) больше длины волны света (λ) – d>λ (в электронных кристаллах d<λ) – сверх решётки.
Для них вводят понятие фотонной запрещенной зоны – фотоны с энергией равной ΔEg не могут распространяться в кристалле.
Сверх решётки I и II рода- металлы (I) или сплавы (II) , у которых сопротивление электрическому току падает до 0 при некоторой критической температуре, явление сверхпроводимости (наблюдают при низких Т)
Фуллерены – сильно пористые структуры (атомы образуют жесткий каркас, остальное пустота)
Электропроводность в твердых телах.
Носители заряда. Подвижность.
Металлы: обладают электронной проводимостью- перенос зарядов осуществляется электронами зоны проводимости – их концентрация
1 э-на/атом.
Диэлектрики и полупроводники – носители зарядов 2-х типов – электроны ЗП и дырки валентной зоны не полностью заполненное электронами.
Проводимость – биполярная.
Дырки – квази частицы обладающие положительным зарядом q+= q- равному по величине заряду электрона.
При возбуждении электрон из валентной зоны в зону проводимости – в валентной зоне возникает свободный уровень (электрическая вакансия).В электрическом поле переход на свободный возможен с уровня ,лежащего под ним. При освобождении только второго Уровня – электрон с 3-го уровня перейдёт на 2-ой.
Такие переходы взаимосвязаны, т.к. ограничены принципом Паули.
Т.о. – возникает перенос заряда за счёт связанных электронов, которых много. Поэтому проводимость по валентной зоне вычисляют ,как перенос положительного заряда небольшим числом фиктивных частиц – дырок (q+= |q-|) по почти заполненной валентной зоне.
Число дырок ≡ числу свободных уровней в валентной зоне.
Дрейфовая подвижность μd.
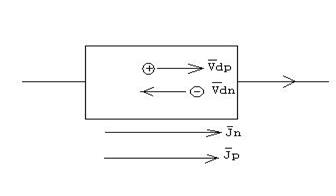
j=jn+jp
Во внешнем электрическом поле E – электроны ускоряются против поля со скоростью дрейфа Vdn, а дырки по полю с Vdp.
Величина, связывающая скорость дрейфа Vd и электрическом поле E – есть дрейфовая подвижность Vd=μdE
μd =|Vd|/|E| - численно равна скорости дрейфа в поле единичной напряженности.
μd =qτ/m* - связана с параметрами носителей – зарядом и эффективной массой
и τ – временем свободного пробега носителей (зависит от механизма рассеяния носителей)
Удельная электропроводность твердого тела. (σ)
Биполярная проводимость.
σ вычисляют с применением закона Ома j=σE
Возьмем изотропный кристалл (j=σE) плотность тока j=jn+jp jn- плотность электрического тока jp- плотность дырочного тока
jn=σnE jp=σpE
σn- электронная проводимость
σp- дырочная проводимость
Вычислим jn и jp
jn=qnin in- плотность потока электронов
jp=qpip ip- плотность потока дырок
Пусть концентрация электронов – n и дырок – p
Тогда: jn=n*1*Vdn=-nμdnE
jp=p*1*Vdp=-nμdpE
jn=-q_*nμdnE=-q+*nμdnE
σn=qnμdn
jp= q+*pμdpE
σn=qpμdp
j=(σn+ σp)E =q(nμn+pμp)E
σ=q(nμn+pμp) –для биполярной проводимости.
n, p – концентрация электронов и дырок.
μn и μp - их дрейфовые подвижности.
Электропроводность чистых (собственных) и легированных (примесных) полупроводников.
Чистый полупроводник(без примесей) n=p=ni
ni – собственная концентрация носителей заряда в полупроводнике.
σ=qni(μn+μp)
ni – расчетная величина (зависит от ΔEg и плотности состояний в зонах Nc и Nv )
Легированный полупроводник – электронные (n- типа) и дырочная (p- типа)
В полупроводниках для управления σ вводят примеси – доноры (источники электронов), акцепторы (источники дырок).
В общем случае σп/п=σn+σp
Уравнение Шредингера для электронной подсистемы кристалла.
Стационарное уравнение Шредингера позволяет определить собственные значения оператора полной энергии кристалла
Н*ψ=Е*ψ
В результате применения адиабатического приближения и введения понятия самосогласованного поля оператор полной энергии (Гамильтониан ) кристалла переходит в Гамильтон T электронов.
Волновая функция кристалла Ψ(ri,Rα)→Ψ(ri,R0α) переходит в волновую функцию электронов R0α – параметр определяющий координаты покоящихся ядер (координаты узлов кристаллической решетки)
Энергия электронов Ee=Ee(R0α) параметрически зависит от R0α
Уравнение Шредингера: ĤΨ (r,Ro)=E (R0α)Ψ (r, R0α) – многоэлектронное уравнение, в общем виде не решается.
Одноэлектронное приближение. Метод самосогласованного поля.
-сводит многоэлектронное уравнение Шредингера к одноэлектронному, введением самосогласованного поля.
Ωi(r)- потенциальная энергия i-го электрона в поле, создаваемом остальными электронами.
Движение i-го электрона и других электронов взаимосвязаны: движение отдельного электрона влияет на движение всей совокупности электронов.
Это позволяет считать движение электронов независимым в некотором поле, равном ∑Ωi(r) и позволяет заменить в уравнении Шредингера энергию взаимодействия электронов Uee на ∑Ωi(r)
Аналогично потенциальную энергию взаимодействия электронов и ядер Uez заменить на сумму энергий отдельных электронов в поле ядер:
Uez=∑Ui(r)
и таким образом Ĥ=∑( -ћ²/2mi▼²i)+∑Ωi(r)+∑Ui(r)=∑(Ĥi)
где Ĥi –гамильтон i-го электрона
Ĥi=-ћ²/2miUi²+ Ωi(r)+Ui(r)
(электроны не взаимодействуют между собой – движения их независимы)
Поэтому волновая функция Ψ=ПΨi .
Где Ψi – волновая функция i-го электрона
Энергия электронов E=∑(Ei)
Ei – энергия i-го электрона
Уравнение Шредингера:
(∑Ĥi)(ПiΨi)=∑(Ei)(ПiΨi) или ĤiΨi=EiΨi – одноэлектронное уравнение Шредингера опустим “i” – т.к. электроны неразличимы.
[-ћ²/2m▼²+ Ω(r)+U(r)]Ψ(r)=EΨ(r)
Учтём симметрию кристалла:
Введем кристаллический потенциал U(r)=Ω(r)+U(r)
U(r) – периодическая функция с периодом кристаллической решетки.
U(r+an)=U(r), an – вектор трансляции решётки.
Периодичность U(r) следует из периодичности распределения плотности электронов, ионизующихся около ядер.
Т.о. одно электронное уравнение Шредингера с учётом симметрии кристалла:
[-ћ²/2m▼²+ Ω(r)+U(r)]Ψ(r)=EΨ(r)
E – разрешенное состояния электронов в кристалле.
Одноэлектронная волновая функция Ψ(r)
Для нахождения электрического спектра электронов необходимо выбрать волновую функцию удовлетворяющую условию трансляционной симметрии кристалла.
Согласно теореме Блоха волновая функция есть: Ψ(r)=Uk(r)e^i(kr)
Т.е. произведение экспоненты ei(rk) определяет фазу электронной волны (волны Блоха) на периодическую функцию
Uk(r)=Uk(r+an) –амплитуда, модулирования по периоду решетки.
Т.о. волновая функция Блоха – плоская бегущая волна с модулированной амплитудой.
k- квази волновой вектор электрона в периодическом поле кристалла U(r) вид функции Uk(r) – зависит от вида U(r)
Условие трансляции.
Ψ(r+an)=ei(k, an)Ψ(r)
Т.е. при смещении электрона на вектор решетки an изменяется фаза. Но фаза не имеет значения при определении физических параметров.
Например: вероятность нахождения электрона в элементе объема dτ около точки r:
W(r)=|Ψ(r)|²dτ ,
при этом U(r)=W(r+an)
Докажем условие трансляции волновой функции.
Запишем r на r+an
Ψ(r+ an)=U(r+ an)ei(k, r+ an)
U(r+ an)=U(r) –автоматически
ei(k, r+ an)= ei(k, an)*e (k,r)
и т.о. Ψ(r+ an)= ei(k, an)*Uk(r)ei(k,r)= ei(k, an)*Ψ(r)
Т.о. электроны свободно перемещаются в кристалле не рассеиваясь, т.е. их движение аналогично движению свободных электронов.
Приближение сильносвязанных электронов (ПСЭ)
- метод линейной комбинации атомных орбиталей (ЛКАО) – метод решения одноэлектронного уравнения Шредингера для электронов в диэлектриках и полупроводниках где валентные электроны сильно связаны с атомными составами (ионами)
В ПСЭ считают, что кристаллы образуют из изолированных атомов в 2 стадии:
- сначала образуют решетку из атомов с расстоянием между атомами d>a (a- const решетки определенной симметрии)
- затем образованную решетку однородно сжимают и доводят d до значения равному a – образуют кристалл нужной симметрии и параметров.
Энергетические состояния электронов атомов – Ea определены из уравнения Шредингера для атомов:
ĤaΨa(r-an)=EaΨa(r-an)
[-ћ²/2m▼²+U(r-an)]Ψa(r-an)=EaΨa(r-an)
U(r-an) – потенциальная энергия электрона для атома с координатой an
r – расстояние электрона до соответственного атома.
Ψa(r-an) – атомная волновая функция (атомная орбиталь) быстро опадающая при удалении электрона от ядра (экспоненциально с расстоянием)
Блоховская волновая функция в ПСЭ.
При образовании кристалла уровня Ea будут вырождены (одинаковы для всех атомов) поэтому волновую функцию электрона, отличную от 0 во всем кристалле, образуют из линейной комбинации атомных волновых функций Ψa (из теории возмущения для вырожденных состояний)
Ψ(r)=∑CnΨa(r-an) ,где Cn=ei(k,an)
Т.е. однородная волновая функция в ПСЭ имеет вид: Ψ(r)=∑ ei(k,an)*Ψn(r-an)
Найдем с её помощью разрешенные состояния E(k) в кристалле.
Решение уравнения Шредингера в ПСЭ.
E(k) определим как среднее значение квантово-механической величины: <E>=(∫Ψ*ĤΨdτ)/(∫Ψ*Ψdτ) интегрирование ведется по основной области кристалла.
<E>=(∫Ψ*[-ћ²/2m+U(r)]Ψdτ)/(∫Ψ*Ψdτ)
Ψ*(r)=∑ ei(k,an)* Ψ(r-am)
am –вектор решетки.
Закон дисперсии E(k) в методах ПСЭ.
E(k) –энергия электрона в разрешенном k –состоянии в энергетической зоне кристалла.
E(k)=<E>=(∫Ψ*[-ћ²/2m+U(r)]Ψdτ)/∫Ψ*Ψdr
Ψ(r)=∑ei(k,an)*Ψa(r-an)
Ψ*(r)=∑ e-i(k,am)*Ψa(r-am) – комплексная сопряженная волновая функция. n≠m
Найдем HΨ=[-ћ²/2m▼²+U(r)]∑ ei(k,an)*Ψa(r-an)
-ћ²/2m▼²Ψa(r-an) – определим из уравнения Шредингера для атома:
ĤaΨa(r-an)= -ћ²/2m▼²Ψa(r-an)+Ua(r-an)Ψa(r-an)=EaΨa(r-an)
-ћ²/2m▼²Ψa(r-an)=[Ea-Ua(r-an)] Ψa(r-an)
E(k)=(∫∑m e-i(k,am)*Ψa*(r-am){Ea+(Ur)-Ua(r-an)}∑n e-i(k,an)*Ψa(r-an)dτ)/(∑n,m ei(k,an-am)∫Ψa*(r-an)Ψa(r-an)dτ)
E(k)=[(Ea(∑n,m ei(k,an-am)∫ Ψa*(r-an)Ψa(r-an)dτ)/(∑n,m ei(k,an-am)∫ Ψa*(r-am)Ψa(r-an)dτ)]+
(∑n,m ei(k,an-am)∫Ψa*(r-an)[U(r)-U(r-an)]Ψ(r-an)dτ)/(∑n,m ei(k,an-am)∫Ψa*(r-am) Ψa(r-an)dτ)
Суммы ∑n,m зависят от n и m не по отдельности, а от разности, поэтому можно положить m=0
Обозначим (r-an) через Pn
E(k)=Ea+[(∑n ei(k,an)*∫ Ψa*(r)[U®-Ua(Pn)] Ψa(Pn)dτ)/((∑n ei(k,an)*∫ Ψa*(r) Ψa*(Pn)dτ)]
Рассмотрим 2 случая , соответственных методу образования кристалла в методе ПСЭ.
1-й Этап образования кристалла: из изолированных атомов с энергией Ea создали решетку нужной симметрии, но с расстояниями между атомами d>a (постоянная решетки кристалла)
В этом случае волновые функции соседних атомов (ближайшего окружения) не перекрываются с волновой функцией выбранного узла (например n=0 – нулевой узел)
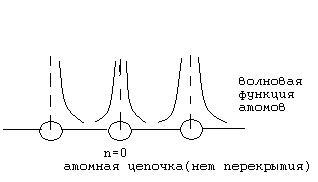
∫Ψ*(к)Ψ(r)dτ=0 n≠0
1 n=0
Для нулевого узла второй член в выражении E(k) будет равен
∫Ψ*(r)[U(r)-Ua(r)] Ψ(r)dτ=-c интеграл отрицательный т.к. U(r)-Ua(r)<0
U(r)- кристаллический потенциал - - -
Ua(r) – атомный потенциал ─
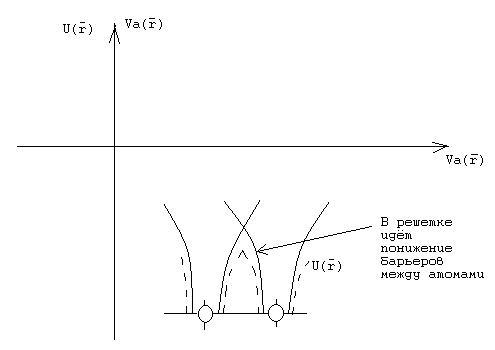
Смысл величины с: есть усредненная энергия электрона рассматриваемого узла (n=0) в поле остальных узлов U(r) за вычетом энергии в данном узле Ua(r)
На величину с понижается каждый уровень в решетке с d>a
При образовании решётки с параметрами d=a атомные волновые функции соседних атомов к нулевому узлу (n=0)- атома 1-ой координационной группы перекрываются (слабо) в полупроводнике и диэлектрике ,благодаря чему, возникает обменное взаимодействие между атомами – электрон туннелирует от атома к атому и принадлежит уже кристаллу в целом.
В результате :вырождение уровней Ea снимается → дискретные уровни Ea – расщепляются в разрешенную зону энергии шириной ΔE
Ширина ΔE определяется величиной обменной энергии:
Обозначим ano – координаты атомов ближайших к нулевому (n=0)
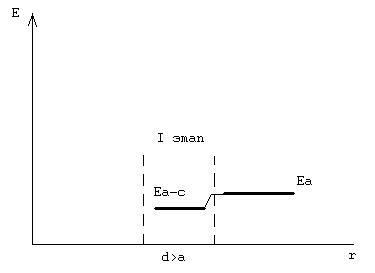
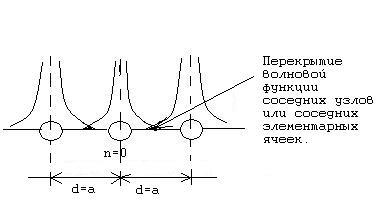
Интеграл перекрытия волновой функции.
∫Ψ*(r)[U®-Ua(Pno)] Ψ*(Pno)dτ=-Ano
(Pno=r-ano)
Ano –определяет величину обменπ энергии при перекрытии волновой функции, отрицательное т.к. U(r)-Ua(Pno)<0
*)E(k)=Ea+[(∑n ei(k,an)*∫ Ψa*(r)[U(r)-Ua(Pno)] Ψa(Pn)dτ)/((∑n ei(k,an)*∫ Ψa*(r) Ψa*(Pn)dτ)]
И т.о. уравнение *) примет вид:
E(k)=Ea-c-∑noei(k,ano)*Ano
Ano – для S- состояния величина изотропная
Ano=A
и E(k)=Eo-c-A∑noei(k,ano)
Применение метода ПСЭ для расчёта E(k) для конкретных решеток.
Кристалл с простой кубической решеткой (ПКР).Направление оси x, y, z по ребрам куба.
Тогда ano=(±a, 0, 0), (0, ±a, 0), (0, 0, ±a)
a - постоянная ПКР
Для расчёта E(k) вычислим
∑noei(k,ano)= ei(kx,a)+ e-i(kx,a)+ ei(ky,a)+ e-i(ky,a)+ ei(kz,a)+ e-i(kz,a)
kx, ky, kz – компоненты волнового вектора k на направления x, y, z в кристалле
E(k)=Ea-c-2A(cos kxa+ cos kya+ cos kza)
Т.е. E(r) – периодическая функция компонент kx, ky, kz в k – пространстве.
Энергия E(k) принимает экстремальные значения при kx=ky=kz=0→Emin=-6A и Emax=+6A(при kx=π/2)
Т.о. имеет место образование разрешенной зоны шириной Emax-Emin=12A(A- модуль)
Образование зоны 12А в ПКР
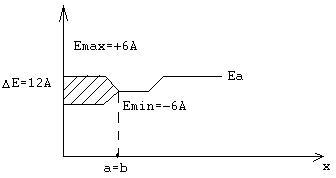
(обычное пространство)
Можно положить Ea-c=0(начало отсчёта энергии)
E(k)=-2A(cos kxa+ cos kya+ cos kza)
в k – пространстве – пространство веществ.
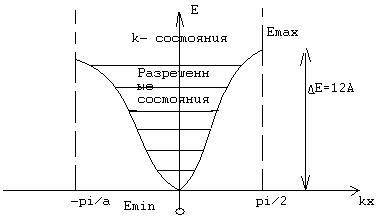
Плотность состояний в разрешенной зоне кристалла конечных размеров.
Дискретность волнового вектора электрона в кристалле.
Реальные кристаллы - имеют ограниченные размеры, т.е. имеют границы. На границах в следствии обрыва химических связей возникают поверхностные состояния.
Для подсчета числа состояний в объемной зоне кристалла используют циклические граничные условия.
Пусть реальный кристалл имеет форму параллепипеда и кубическую решетку.
Размеры ребер Lx, Ly, Lz
Постоянная решетки – a
Длина ребер Lx=Nxa
Ly=Nya
Lz=Nza
Nx, Ny, Nz –число атомов, которое укладывается на ребре.
Для исключения влияния границ на энергетический спектр электронов в объемной зоне используют циклические граничные условия, которые заменяют эквивалентность физических состояний при образовании из кристалла объемом LxLyLz кристалла бесконечных размеров, т.е. все пространство заполнено кристаллом LxLyLz.
Эквивалентность функции состояний в точках (x, x+Lx), (y+Ly), (z+Lz) означает, что волновые функции элементов в этих точках эквивалентны, т.е. они обладают периодичностью с периодом бесконечного кристалла (трансляция).
Докажем это:
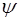 (x+LX, y, z) =
(x+LX, y, z) = 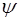 (x, y+Ly, z) =
(x, y+Ly, z) = 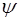 (x, y, z+Lz) - циклические граничные условия.
(x, y, z+Lz) - циклические граничные условия.
Плоская бегущая волна:
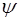 (x+LX, y, z) = U
(x+LX, y, z) = U 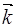 (x+LX, y, z)
(x+LX, y, z) 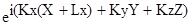
где: 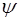 (x+LX, y, z) -функция Блоха
(x+LX, y, z) -функция Блоха
U 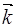 (x+LX, y, z) -амплитуда электронной волны
(x+LX, y, z) -амплитуда электронной волны
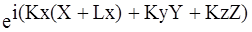 -фазовый множитель
-фазовый множитель
U 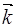 (x+LX, y, z) = U
(x+LX, y, z) = U 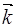 (x, y, z) -“автоматически” (функция периодичная)
(x, y, z) -“автоматически” (функция периодичная)
exp → 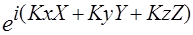
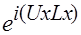 т.е.
т.е.
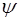 (x+LX, y, z) = U
(x+LX, y, z) = U 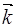 (x, y, z)
(x, y, z) 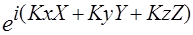
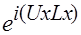 или
или
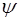 (x+LX, y, z) = U
(x+LX, y, z) = U 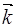 (
( 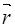 )
) 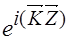
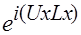
Чтобы функции совпали 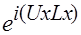 должна быть равна нулю.
должна быть равна нулю.
Мнимая exp = 1, когда показатель равен 2П -целое число; т.е. 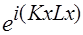 =
= 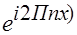 , где Ux -целое число, т.е.
, где Ux -целое число, т.е. 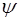 (x+LX, y, z) = U
(x+LX, y, z) = U 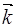 (
( 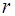 )
) 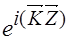 -функция периодическая
-функция периодическая
Где: U 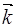 (
( 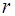 )
) 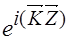 -функция Блоха
-функция Блоха
Из этого следует, что компоненты волнового вектора электроны:
Kx =  nx аналогично Ky =
nx аналогично Ky = 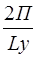 ny, Kz =
ny, Kz = 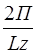 nz
nz
Дискретность компонент Ux, Ky, Kz на направлениях x, y, z приводит к дискретности энергии электрона в зоне и энергия в зоне изменяется не непрерывно, а квазинепрерывно.
Для определения плотности состояний в зоне необходимо из набора nx, ny, nz выделить их значения отвечающие физически различным (неэквивалентным) состояниям в зоне.
Используя в.ф. метода ПСЭ одномерного случая: 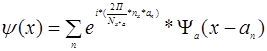 вычислим
вычислим 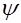 x для разных nx:
x для разных nx:
Если nx = 0, то в.ф. совпадает с.в.ф. для nx = Nx
Если nx = 1, то в.ф. совпадает с.в.ф. для nx = Nx+1
Т.е nx принимает для физ. Неэквивалентных состояний значения от ноля до Nx
Или 0 ‹  nx ‹ Nx ;
nx ‹ Nx ; 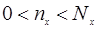 ;
; 
Комп. 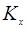 :
: 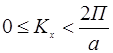 или
или 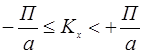
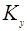 :
: 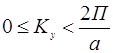 ;(
;( 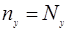 ) или
) или 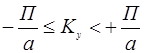
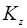 :
: 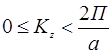 ;(
;( 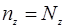 )или
)или 
Т.о волновой вектор электрона в зоне огранич. кристалла принимает 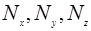 -значений
-значений
это есть число атомов в кристалле для примитивной решетки, для сложной решетки -число элементарных ячеек.
Квазиимпульс ( 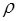 ) электрона в периодическом поле кристалла
) электрона в периодическом поле кристалла
Для описания динамики электрона в кристалле вводят понятие квазиимпульса
(почти импульса 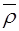 который является
который является
аналогом импульса.
 своб. электрона квазиимпульс
своб. электрона квазиимпульс 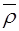 =
= 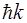 , имеет сходные и отличительные свойства от
, имеет сходные и отличительные свойства от  .
.
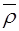 имеет одинаковую размерность с импульсом
имеет одинаковую размерность с импульсом  .
.
Так же, как и импульс  квазиимпульс является интегралом движения:
квазиимпульс является интегралом движения: 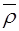 сохраняется во времени, т.е. не изменяется под действием сил со стороны поля кристалла (т.е. внутреннего поля).
сохраняется во времени, т.е. не изменяется под действием сил со стороны поля кристалла (т.е. внутреннего поля). 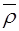 изменяется под действием внешних полей
изменяется под действием внешних полей 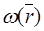 ,не обладающих периодичностью кристалла (электр. и магн.)
,не обладающих периодичностью кристалла (электр. и магн.)
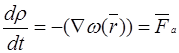 -внешняя сила
-внешняя сила
Отличия - квазиимпульс дискретен 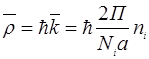 , квазиимпульс
, квазиимпульс  определен неоднозначно, т.е. волновая функция электрона является периодичной функцией в пространстве импульсов, совпадающим с пространством обратной решетки, отличаясь масштабом.
определен неоднозначно, т.е. волновая функция электрона является периодичной функцией в пространстве импульсов, совпадающим с пространством обратной решетки, отличаясь масштабом.
Пусть 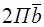 есть вектор обратной решетки, тогда состояние электрона с волновым вектором и
есть вектор обратной решетки, тогда состояние электрона с волновым вектором и 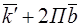 -физически эквивалентны.
-физически эквивалентны.
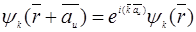
Заменим 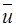 на
на 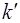 :
:
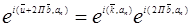
Период трансляции в.ф. в 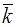 -пространстве есть
-пространстве есть 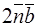 -вектор отр .решетки, т.е в.ф.-периодическая функция в обычном и
-вектор отр .решетки, т.е в.ф.-периодическая функция в обычном и 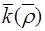 пространствах будут периодичны
пространствах будут периодичны
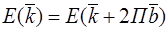
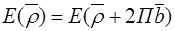
Вывод: квазиимпульс 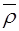 определен с точностью
определен с точностью 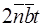
Дата добавления: 2015-08-26; просмотров: 1415;
