Уравнение Шредингера реального кристалла. Метод эффективной массы. Локализованные состояния. Водородоподобные примеси и экситоны.

Электронные состояния в кристаллах с нарушением периодичности кристаллического поля

Нарушение периодичности кристаллического поля U (r ) может быть вызвано различными дефектами кристаллической структуры (примеси, собственные точечные дефекты, дислокации, границы зерен).

Предположим, что W( r ) – поле, которое связано с нарушением кристаллического поля.

Метод эффективной массы

Позволяет решить уравнение Шредингера при наличии нарушения кристаллического поля –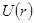

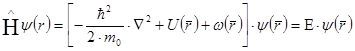
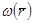- главный потенциал, не обладает периодичностью кристаллического поля .

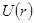Вид функции 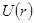– неизвестен. Но 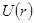можно исключить из уравнения Шредингера, используя эффективную массу электронов - m*, определенной из эксперимента.

Предположим, что 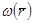=0 и запишем уравнение Шредингера для электронных состояний вблизи экстремума энергии

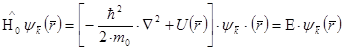
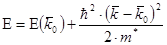– вблизи экстремума электрон ведет себя как свободный, но с эффективной массой.

m* ¹ m₀

Гамильтониану 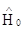можно ввести эквивалентный гамильтониан: 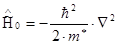, который имеет тот же набор собственных значений, что и 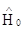, но вместо m₀ использовано m*.

Вместо одноэлектронного уравнения Шредингера можно ввести ему эквивалентные: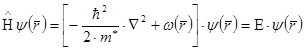

- Уравнение эффективной массы, в котором нет кристаллического потенциала 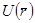.Решение задач на основе этого уравнения получило название метода эффективной массы.

Метод справедлив для электронных состояний, где можно применять m*, то есть вблизи экстремумов энергии.

Изменение в спектре энергии электронов при наличии возмущения его движения - :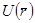

- в запрещенной зоне кристалла возникают разрешенные уровни (состояния) энергии, локализованные в отчасти нарушения кристаллического поля. Поэтому эти состояния называются локализованными, а уровни – локальными.

Волновая функция локализованных состояний отлична от нуля в области нарушения поля кристалла.

Локальные уровни в запрещенной зоне E_t возникают в результате отщепления уровней от потолка зоны – уровни акцепторов (возмущение 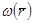> 0), а от дна зоны – уровни доноров ( 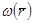< 0).

(рис.5)