Раздел 4. Статистика равновесных носителей заряда

4.1 Распределение электронов и дырок по квантовым состояниям в главных энергетических зонах кристалла. Уровень Ферми. Поверхность Ферми. Плотность квантовых состояний для энергетических зон с изотропным и анизотропным законом дисперсии.

4.2 Концентрация электронов и дырок в зонах для различных степеней вырождения электронного или дырочного газа.

4.3 Статистика примесных состояний. Функция распределения электронов и дырок по примесным состояниям. Плотность примесных состояний. Примесные зоны. Влияние температуры и концентрации примеси на концентрацию свободных электронов и дырок.

4.4 Плотность квантовых состояний в квантово-размерных структурах с квантовыми ямами, квантовыми нитями и квантовыми точками.

Распределение электронов и дырок по квантовым состояниям в главных энергетических зонах кристалла. Уровень Ферми. Поверхность Ферми. Плотность квантовых состояний для энергетических зон с изотропным и анизотропным законом дисперсии.

Для определения s твердого тела необходимо знать равновесную (темновую) концентрацию электронов (n) и дырок (p).

Для определения n и p необходимо знать параметры зон – плотность квантовых состояний и вероятность их дополнения – функцию распределения электронов и h⁺ по состояниям.

Функции распределения электронов и дырок по квантовым состояниям разрешения зон (зона проводимости и валентная зона).

Электроны в металлах, полупроводниках подчиняются квантовой статистике. Вероятность заполнения уровня E при температуре T определяется функцией Ферми – Дирака:

Электроны проводимости – фермионы – частицы, обладающие полуцелым спином, и подчиняются принципом Паули:

F – уровень (энергия) Ферми, или электрохимический потенциал.

Основные свойства функции f_Ф-Д :

При T ® 0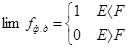

При T = 0 функция терпит разрыв (то есть функция не определена).

Из графика следует, что f есть уровень, который разделяет занятые электронами состояния в зоне проводимости от свободных.

В металлах при T = 0: уровень F соответствует максимальной энергии электронов в зоне проводимости – энергии Ферми.

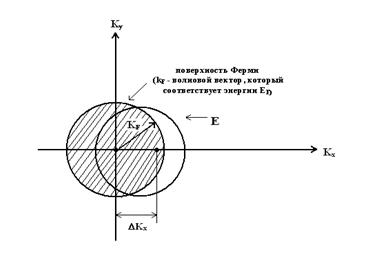
В 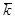- пространстве вводят

поверхность Ферми,

которая соответствует энергии E_F.

Внутри сферы Ф – находятся электроны проводимости.

Проводимость по зоне проводимости - есть жесткое смещение сферы Ф в - пространстве под действием внешнего электрического поля на величину Dk_x.

При температурах T > 0:

f_Ф-Д = 0,5 и F имеет смысл уровня, вероятность заполнения которого ½.

Функция f_Ф-Д претерпевает наибольшее изменение для энергий вблизи F.

При (E – F) >> kT функция f_Ф-Д переходит в классическую функцию Максвелла – Больцмана:

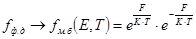– это высокоэнергетический хвост функции f_Ф-Д.

Уровень F ниже Ec на энергию не меньше kT.

В этом случае действует классическая статистика Максвелла – Больцмана и полупроводников, подчиняющиеся этой статистике – невырожденные (по концентрации).

Невырожденный полупроводник n-типа – полупроводник, в котором уровень F лежит ниже Ec в запрещенной зоне на величину не меньше kT.

Таким образом, в невырожденном полупроводнике на уровне f – нет электронов в отличие от металла!

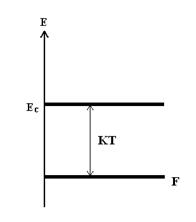
Невырожденный полупроводник p-типа – уровень F лежит выше Ec на величину kT.

Плотность состояний N(E)

- это число квантовых состояний в зоне, приходящихся на единичный интервал энергии в кристалле единичного объема.

Предположим, что в интервале энергии: (E,E + dE) находится dS состояний.

Тогда для кристалла единичного объема: dS = N(E)dE пропорционально dE

N(E) = dS/dE – плотность состояний.

N(E) связана с формой поверхности равной энергии.

Интервалу dE соответствует шаровой слой объема , которым выделяют поверхности равной энергии:

E, E + dE = const

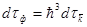
Число состояний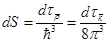

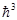- объем, приходящий на одно состояние.

Плотность состояний в зоне проводимости

Эффективная масса – скалярная величина m_n

N(E) = dS/dE dS – число состояний в интервале E, E + dE в кристалле единичного объема.

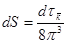
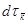- элемент объема 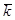- пространства, заключается между поверхностями равной энергии.

E = const и E +dE = const

Найдем 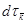, используя закон дисперсии для полупроводника с изотропной эффективной массой электрона m_n

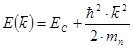
Поверхности E, E + dE заключают объем 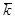- пространства

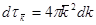
(поверхности – сферы; 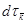- шаровой слой)

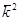- найдем из закона дисперсии:

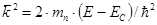
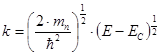
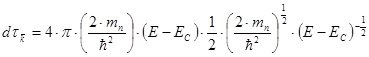
Таким образом

Для изотропной валентной зоны: (m_p – эффективная масса дырки)

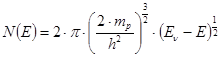
Таким образом, плотность состояний пропорциональна:

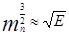
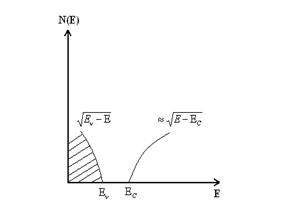
Зонная модель прямозонного полупроводника с использованием функций N(E)

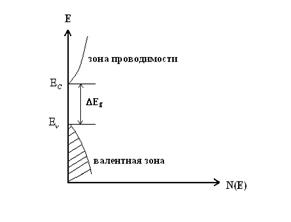
Используется в физике полупроводниковых приборов.

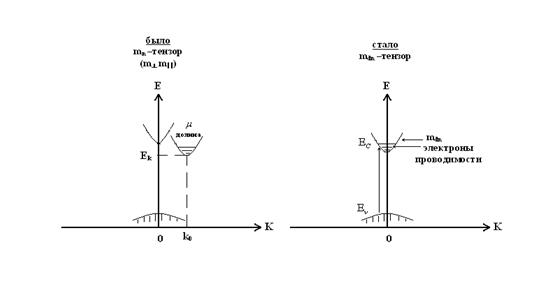
Плотность состояний в зоне проводимости многодолинного (непрямозонного) полупроводника

Эффективная масса m_n - тензорная величина.

Закон дисперсии 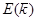- анизотропная квадратичная величина:

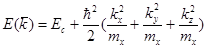
m_C^-1, m_U^-1, m_Z^-1 – компоненты эффективной массы.

Поверхности равной энергии – эллипсоидальные с полуосями.

a, b, c:

(j = x, y, z)

Объем эллипсоида: V = 4/3p * a b c

Объем , которым выделяют поверхности E и E + dE = const находят как приращение объема dV.

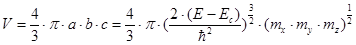
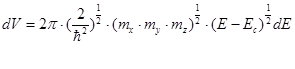
Таким образом, для одной долины:

N(E) = 2p (m_x m_y m_z)^1/2 (2/h)^3/2 (E – Ec)^1/2

Для m-долин:

N(E) =m * 2p (m_x m_y m_z)^1/2 (2/h²)^3/2 (E – Ec)^1/2

Приведем эту формулу к виду для прямозонного полупроводника.

Для этого введем понятие эффективной массы для плотности состояний m_nd:

N(E) = 2p (2 m_nd / h²) ^3/2 (E – Ec)^1/2

где m_nd = m^2/3 (m_x m_y m_z)^1/2

Если поверхности – эллипсоиды вращения (электроны в Ge, Si)

m_x = m_y = m_^, m_z =m_ïï

Таким образом, m_nd = m^2/3 (m²_^ m_ïï)^1/2\

m_^ и m_ï½ определяется из эксперимента по циклотронному резонансу.

Смысл введения m_nd

Позволяет многодолинную зону проводимости с анизотропной эффективной массой mn записать параболичной зоной с изотропной массой с одним абсолютным минимумом (нужно для вычисления концентраций).