Пример расчета рангового коэффициента корреляции
Пусть при исследовании десяти человек получены следующие показатели Х и Y. Выясним, существует ли между ними связь. Для этого подсчитаем ранговый коэффициент корреляции и дадим его графическую интерпретацию.
Таблица 3
| Х | Y |
Найдем ранг (порядковый номер по убыванию) каждого из значений х и у: Rx и Ry, затем найдем разности соответствующих рангов d, возведем их в квадрат, получим ряд значений d2. Если значения одинаковые, то приписывается промежуточный средний ранг, например, 6,5.
Просуммируем их и подставим в формулу:
rs=1- 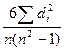 .
.
Таблица 4
| № | X | Y | Rx | Ry | |d| | d2 |
| Сумма: |
В нашем случае: rs=1- 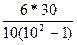 =0,81.
=0,81.
Оценим значимость коэффициента корреляции
tфакт.= 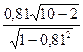 =3,92.
=3,92.
По таблице 5 Приложения 2 определяем, что для уровня значимости р=0,05 tкрит.=2,31. Следовательно, вычисленный коэффициент корреляции значимо отличается от нуля и между показателями х и у наблюдается линейная связь выше среднего.
Для графической интерпретации по оси х откладываются значения признака х, по оси у – значения признака у.
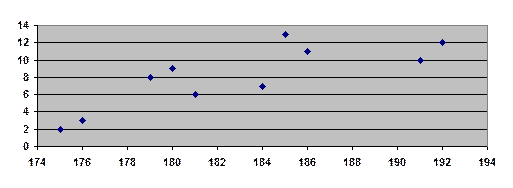
рис.6. Графическая интерпретация коэффициента корреляции.
По значению коэффициента корреляции и графической интерпретации можем сказать, что между признаками х и у есть средняя прямая связь.
Дата добавления: 2015-08-21; просмотров: 726;
