Пример построения интервального вариационного ряда
Пусть измерен некоторый экономический показатель в 30 регионах:
23 29 35 7 11 18 23 30 36 18 11 8 13 20 25 27 14 30 20 20 24 19 21 26 22 16 26 25 33 27
Расставим экспериментальные данные в возрастающем порядке:
6 8 11 11 13 14 16 18 18 19 20 20 20 21 22 23 23 24 25 25 26 26 27 27 29 30 30 33 35 36
По таблице 1 определяем число классов
Таблица 1
| Объем выборки n | Число классов K |
| 6-11 | |
| 12-22 | |
| 23-46 | |
| 47-93 | |
| 94-187 | |
| 188-377 | |
| 378-755 | |
| 756-1515 |
Для n=30 число классов K=6. Найдем минимальное и максимальное значения вариант: хmin=7, хmax=36. Определим вариационный размах R= хmin-хmax=36-6=30.
Определим величину классового интервала: D= 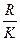 =
=  =5.
=5.
Хн1= хmin=6; Хв1= хmin+D=6+5=11
Обобщим полученные данные в таблице:
Таблица 2
| Номера классов | Классовые интервалы | Серединные значения классов | Частоты | Накопленные частоты |
| 6-11 | 8,5 | |||
| 11-16 | 13,5 | |||
| 16-21 | 18,5 | |||
| 21-26 | 23,5 | |||
| 26-31 | 28,5 | |||
| 31-36 | 33,5 |
График, называемый гистограммой получается, если в прямоугольной системе координат отложить по оси абсцисс границы классов, а по оси ординат их частоты.
Если серединные точки вершин прямоугольников гистограммы соединить между собой, получится график дискретного варьирования, называемый полигоном распределения.
1.2. Мода распределения – это наиболее часто встречающееся значение ряда.
1.3. Среднее арифметическое распределения находится по формуле
хср= (х1+х2+х3+ …+хn)/n
1.4. Дисперсия распределения находится по формуле:
D= 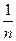
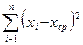
1.5. Стандартное отклонение S= 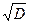
Дата добавления: 2015-08-21; просмотров: 1175;
