Организация мультипроцессорных систем.
Один из самых простых способов организации мультипроцессорных систем опирается на использование общей шины (рис. 3.10), к которой подключаются процессоры и память.
Процессоры Общая память
пр пр пр Память
гч гч /\ /\
\|------------------------------------------- 1^
Шина
Рис. 3.10. Мультипроцессорная система с общей шиной
Сама шина состоит из какого-то числа линий, необходимых для передачи адресов, данных и управляющих сигналов между процессорами и памятью. Чтобы предотвратить одновременное обращение нескольких процессоров к памяти,
используются та или иная схемы арбитража, гарантирующие монопольное владение шиной захватившим ее устройством. Основная проблема таких систем заключается в том, что даже небольшое увеличение числа устройств на шине (4-5) очень быстро делает ее узким местом, вызывающим значительные задержки при обменах с памятью и катастрофическое падение производительности системы в целом.
Для построения более мощных систем необходимы другие подходы. Одним из решений является разделение памяти на независимые модули и обеспечение возможности доступа разных процессоров к различным модулям одновременно, в
частности, использование матричного коммутатора. Процессоры и памяти связываются так, как показано на рис. 311.
Модули памяти
модули
HID
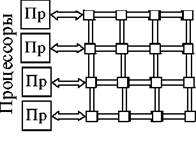
Точечные переключатели Рис. 3.11. Мультипроцессорная система с матричным коммутатором
| На |
| пересечении |
| линий |
| эасполагаются |
| точечные |
элементарные
переключатели, разрешающие или запрещающие передачу информации между процессорами и модулями памяти. Безусловным преимуществом такой организации является возможность одновременной работы процессоров с различными модулями памяти. Естественно, в ситуации, когда два процессора захотят работать с одним модулем памяти, один из них будет заблокирован. Недостатком матричных коммутаторов является большой объем необходимого оборудования, поскольку для связи л процессоров с л модулями памяти требуется л2 элементарных переключателей. Во многих случаях это является слишком дорогим решением, что вынуждает разработчиков искать иные пути.
| способом |
| является |
| использование |
| каскадных |
Альтернативным
переключателей, например, так, как это сделано в омега-сети. На рис. 3.12 показана сеть коммутаторов 2x2, организованная в два каскада.
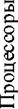
|
 Пр
Пр
Пр
Пр
Пр
Lt;d
Lt;d
^>
^>
Память
Память
Память
Память
Переключатели 2x2 Рис. 3.12. Мультипроцессорная система с омега-сетью
Каждый использованный коммутатор может соединить любой из двух своих входов с любым из двух своих выходов. Это свойство и использованная схема коммутации позволяют любому процессору вычислительной системы, показанной на этом рисунке, обращаться к любому модулю памяти. В общем случае для соединения л процессоров с л модулями памяти потребуется logzn каскадов по л/2 коммутаторов в каждом, т. е. всего (nlogzn)/2 коммутаторов. Для больших значений л эта величина намного лучше, чем п2, однако появляется проблема другого рода - задержки. Каждый коммутатор не срабатывает мгновенно, т. к. на коммутацию входа с выходом на каждом каскаде требуется некоторое время. Ищется компромисс между дорогой коммуникационной системой с небольшим временем переключения и недорогой системой, но с большими задержками.
|
|
а)
в)
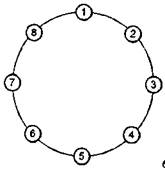
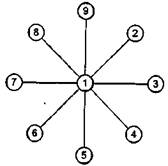
б) Рис. 3.13. Мультикомпьютерные системы с топологиями связи: а - линейка; б - кольцо; в - звезда
Реально используемых схем коммутации процессоров в системах с распределенной памятью намного больше. По существу можно использовать и все уже рассмотренные варианты, и одновременно массу других. Простейший вариант
топологии связи показан на рис. 3.13, а, где все вычислительные узлы объединены в одну линейку-Каждый узел системы, кроме первого и последнего, имеет по одному непосредственному соседу справа и слева. Для построения системы из л узлов требуется л-1 соединений. Средняя длина пути между двумя узлами системы равна л/3. Можно уменьшить среднюю длину пути, если преобразовать линейку вычислительных узлов в кольцо (рис. 3.13, б). Добавив лишь одно дополнительное соединение первого узла с последним, можно получить два дополнительных полезных свойства у новой топологии. Во-первых, средняя длина пути между двумя узлами сократилась с л/3 до л/6. Во-вторых, за счет того, что передача между любыми узлами уже может идти по двум независимым направлениям, увеличилась отказоустойчивость системы в целом. Пока все связи работоспособны, передача будет идти по кратчайшему пути. Но если нарушилась какая-либо одна связь, то возможна передача в противоположном направлении.
Несмотря на явную ограниченность в непосредственных связях даже подобные простые "линейные" топологии хорошо соответствуют многим алгоритмам, в которых необходима связь лишь соседних процессов между собой. В частности, многие одномерные задачи математической физики хорошо решаются подобными методами. Для таких задач никаких других топологий придумывать не надо. Но далеко не все задачи такие. Схему сдваивания или блочные методы линейной алгебры на таких топологиях эффективно реализовать не просто, поскольку неправильное размещение процессов по процессорам приведет к потере большей части времени на коммуникации. В идеальной ситуации пользователь не должен думать об этом. Сегодня по технологическим причинам нельзя сделать большие мультикомпьютерные системы, в которых каждый процессор имел бы непосредственную связь со всеми остальными. Поэтому разработчикам вычислительных систем приходится искать компромисс между универсальностью и специализированностью, между сложностью и доступностью. Если класс задач заранее определен, то ситуация сильно облегчается, и результат может быть найден легко. Например, использование схемы распределения работы между параллельными процессами, аналогичной схеме клиент-сервер, при которой один головной процесс раздает задания подчиненным процессам (схема мастер/рабочие, или master/slaves), хорошо соответствует топологии "звезда" (рис. 3.13, в).
Вычислительные узлы, расположенные в лучах звезды, не имеют непосредственной связи между собой. Но это нисколько не мешает эффективному взаимодействию процесса-мастера с подчиненными процессами при условии, что мастер расположен в центральном узле.
Выбор той или иной топологии связи процессоров в конкретной вычислительной системе может быть обусловлен самыми разными причинами. Это могут быть соображениями стоимости, технологической реализуемости,
простоты сборки и программирования, надежности, минимальности средней
длины пути между узлами, минимальности максимального расстояния между узлами и др. Некоторые варианты показаны на рис. 3.14.
|
|
а)
б)
|
 в)
в)
г)
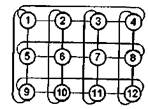
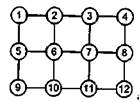
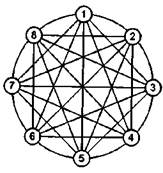
Рис. 3.14. Варианты топологий связи процессоров: а -решетка; б - 2-тор; в - полная связь; г - гиперкуб
Топология двумерной решетки (рис. 3.14, а) была использована в начале 90-х годов прошлого века при построении суперкомпьютера Intel Paragon на базе процессоров i860. В соответствии с топологией двумерного тора (рис. 3.14, б) могут быть соединены вычислительные узлы кластеров, использующих сеть SCI, предлагаемую компанией Dolphin Interconnect Solutions. В настоящее время эта же компания Dolphin предлагает сетевые комплекты, позволяющие объединять узлы в трехмерный тор - чем меньше среднее расстояние между узлами, тем выше надежность. В этом смысле наилучшие показатели имеет топология, в которой каждый процессор имеет непосредственную связь со всеми остальными (рис. 3.14,
в)
Иногда находятся исключительно интересные варианты, одним из которых является топология двоичного гиперкуба (рис. 3.14, г). В n-мерном пространстве рассмотрим лишь в вершинач единичного n-мерного куба размещаются процессоры системы, т. е. точки (x±_, xz, .... х„), в которых все координаты х, могут быть равны либо 0, либо 1. Каждый процессор соединим с ближайшим
| п |
| измерений. В |
| эезультате |
непосредственным соседом вдоль каждого из
получается л-мерный куб для системы из N = 2" процессоров. Двумерный куб соответствует простому квадрату, а четырехмерный вариант условно изображен на рис. 3.14, г. В гиперкубе каждый процессор связан лишь с log2N
непосредственными соседями, а не с N, как в случае полной связности. Гиперкуб имеет массу полезных свойств. Например, для каждого процессора очень просто определить всех его соседей: они отличаются от него лишь значением какой-либо одной координаты х. Каждая "грань" л-мерного гиперкуба является гиперкубом размерности л-1. Максимальное расстояние между вершинами л-мерного гиперкуба равно л. Гиперкуб симметричен относительно своих узлов: из каждого узла система выглядит одинаковой и не существует узлов, которым необходима специальная обработка.
Дата добавления: 2015-08-21; просмотров: 1613;
