Параллелизм независимых ветвей.

Суть параллелизма независимых ветве состоит в том, что в программе решения большо задачи могут быть выделены независимые программные части — ветви. Под независимостью ветве в первую очередь понимается независимость по данным.

В параллельных языках запуск параллельных ветве осуществляется с помощью оператора FORK Ml, М2 , ..., ML, где Ml, М2, ..., ML — имена независимых ветве. Каждая ветвь заканчивается оператором JOIN (R,K), выполнение которого вызывает вычитание единицы из ячейки памяти R. Так как в R предварительно записано число, равное количеству ветве, то при последнем срабатывании оператора JOIN (все ветви выполнены) в R оказывается нуль и управление передается на оператор К. Иногда в JOIN описывается подмножество ветвей, при выполнении которого срабатывает этот оператор. В последовательных языках аналогов операторам FORK и JOIN нет и ветви выполняются друг за другом. Рассмотрим пример задачи с параллелизмом ветве.

Параллелизм вариантов

Это широко распространенны в практике вариант решение одной и то же модели при разных входных параметрах, причем, все варианты (как правило, с длительным счетом) должны быть получены за ограниченное время. Например, варианты моделирования используются при анализе атмосферной модели климата, при расчете ядерного взрыва, обтекания летательного аппарата, расчета полупроводниковых приборов.

Параллелизм вариантов отличается от идеологии крупнозернистого параллелизма. Отличие состоит в том, что в случае крупнозернистого параллелизма вычисления проводятся внутри одно задачи и требования к скорости обмена между частями задачи достаточно высокие. В параллелизме вариантов распараллеливаются целые задачи, обмен между которыми в принципе отсутствует.

Системы распределенных вычислений идеальны для решения вариантных задач. Закон Амдала.

Одной из главных характеристик параллельных систем является ускорение R параллельной системы, которое определяется выражением:

R = Ti /Т_п,

где Т^ - время решения задачи на однопроцессорной системе, а Тп - время решения той же задачи на п - процессорной системе.

Пусть W = W^ + Wij,, где W - общее число операций в задаче, W_m - число операций, которые можно выполнять параллельно, a W_g - число скалярных (нераспараллеливаемых) операций.

Обозначим также через t время выполнения одной операции. Тогда получаем известный закон Амдала [13]:

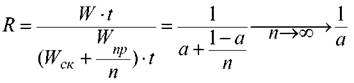
Здесь а = W^ /W - удельный вес скалярных операций.

Закон Амдала определяет принципиально важные для параллельных вычислени положения:

•S ускорение зависит от потенциального параллелизма задачи (величина 1- а) и параметров аппаратуры (числа процессоров п).

S предельное ускорение определяется свойствами задачи.

Пусть, например, а = 0,2 (что является реальным значением), тогда ускорение не может превосходить 5 при любом числе процессоров, то есть максимальное ускорение определяется потенциальным параллелизмом задачи. Очевидной является чрезвычайно высокая чувствительность ускорения к изменению величины а.