Определение момента инерции дополнительной маховой массы (маховика).
Рассмотрим определение маховика для примера рассмотренного в лекции 6 - одноцилиндрового поршневого насоса. В первую группу звеньев в этом примере входят: ротор электродвигателя Iрот, детали редуктора I прред, кривошипный вал I01 и маховик Iм
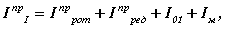
откуда момент инерции маховика
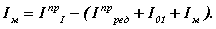
Определение момента инерции маховика по методу Н.И.Мерцалова.
При расчете маховика (или решении задачи регулирования хода машины) по методу Н.И.Мерцалова задача решается в следующей последовательности:
- Определяются параметры динамической модели, например для ДВС Мпрд - приведенный суммарный момент движущих сил и IпрII - приведенный момент инерции второй группы звеньев.
- Определяется работа движущих сил Ад интегрированием функции Мпрд = f(j 1) за цикл движения машины (допустим 2p );
- Определяется работа движущих сил за цикл и приравнивается к работе сил сопротивления Адц = Асц. Из этого равенства определяется среднеинтегральное значение момента сил сопротивления
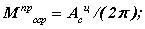
и для него строится диаграмма работы Ас = f(j 1). Суммированием этой диаграммы и диаграммы Ад = f(j 1) получаем диаграмму А = f(j 1).
- Делается допущение w 1 » w 1ср , при котором TII » IпрII *w 1ср2/ 2 (первое допущение метода Мерцалова), и определяется TII = f(j 1).
- Определяется кинетическая энергия первой группы звеньев
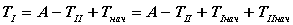
Так как начальные значения кинетической энергии неизвестны, то если учесть, что 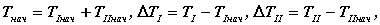 , получим
, получим
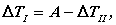
то есть, вычитая из суммарной работы приращение кинетической энергии второй группы, получим приращение кинетической энергии первой группы.
По функции DTI = f(j 1) определяется максимальное изменение кинетиской энергии за цикл D TImax . Второй раз делаем допущение w1 » w 1ср на основании которого, как показано выше, можно записать
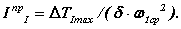
Из этого выражения, определив предварительно DTImax , можно решить две задачи:
- задачу синтеза - при заданном [d ] определить необходимый для его обеспечения приведенный момент инерции IпрI нб ,
- задачу анализа - при заданном IпрI определить обеспечиваемый им коэффициент неравномерности d .
Алгоритм определения момента инерции маховика при установившемся режиме движения машины.
Решение этой задачи рассмотрим на конкретном примере машинного агрегата привода буровой установки.
Дано: Кинематическая схема машины - lAB = 0.12м, lBC = 0.528м, lBS2 = 0.169м, средняя частота вращения кривошипа - w 1ср = 47.124 рад/с2, массы звеньев -
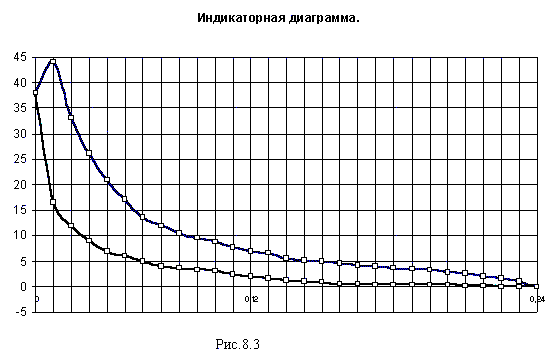
m2 = 24.2 кг, m3 = 36.2 кг, момент инерции - I 2S = 1.21 кг* м2, I 10 = 2.72 кг* м2, максимальное давление в цилиндре - pmax = 4.4 МПа , коэффициент неравномерности вращения [d ] = 1/80 , индикаторная диаграмма (приведена на рис. 8.3) .
_________________________________________________________________
Определение момента инерции махового колеса
- Определение параметров машины: Мпрд - приведенного суммарного момента движущих сил и IпрII - приведенного момента инерции второй группы звеньев.
|
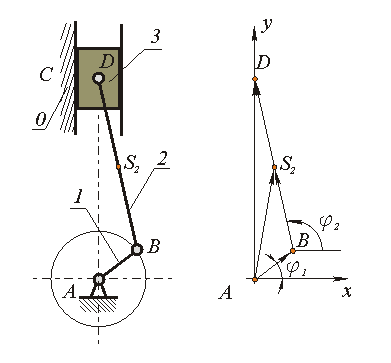
|
Рис. 8.4
1.1. Определение приведенного момента движущих сил Мпрд .
Индикаторную диаграмму (рис.8.3) строим по заданным значениям давления в цилиндре двигателя. Отрезок хода поршня НC* m i делим на 10 интервалов. В каждой точке деления строим ординату диаграммы, задавшись (при pi /pmax = 1) максимальной ординатой ypmax . Тогда текущее значение ординаты
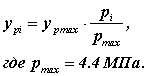
Масштаб индикаторной диаграммы
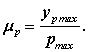
Площадь поршня 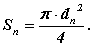
При построении графика силы, действующей на поршень, ординаты этого графика принимаем равными ординатам индикаторной диаграммы. Тогда масштаб силы
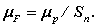
Для исследуемого механизма приведенный суммарной момент состоит из двух составляющих: движущей силы и момента сил сопротивления
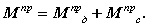
Приведенный момент движущей силы определяется в текущем положении механизма по формуле
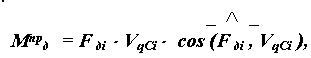
|
где F дi - значение движущей силы,
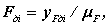
где yFдi - ордината силы сопротивления,
m F - масштаб диаграммы сил.
VqСi - значение передаточной функции в рассматриваемом положении механизма,
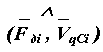
|
- угол между вектором силы и вектором скорости точки ее приложения.
|
Рис. 8.6
Масштаб диаграммы по оси абсцисс определяется по формуле
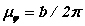
где b - база диаграммы ( отрезок оси абсцисс, который изображает цикл изменения обобщенной координаты).
1.2. Построение диаграммы приведенных моментов инерции Ivпр = I IIпр.
Инерционные характеристики звеньев механизма в его динамической модели представлены суммарным приведенным моментом инерции. При расчете эту характеристику динамической модели представляетсяв виде суммы двух составляющих переменной Ivпр = I IIпр и постоянной Icпр = IIпр. Первая определяется массами и моментами инерции звеньев, передаточные функции которых постоянны, вторые - массами и моментами инерции звеньев передаточные функции которых переменны.
Проведем расчет переменной части приведенного момента инерции Ivпр = I IIпр. Для рассматриваемого механизма во вторую группу звеньев входят звенья 2 и 3. Звено 3 совершает поступательное движение, звено 2 -плоское. Расчет переменной части приведенного момента проводится по следующим зависимостям:
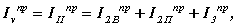
где
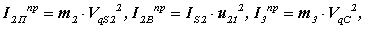
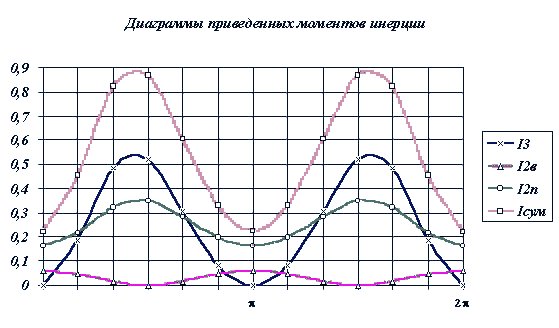
|
Рис. 8.7
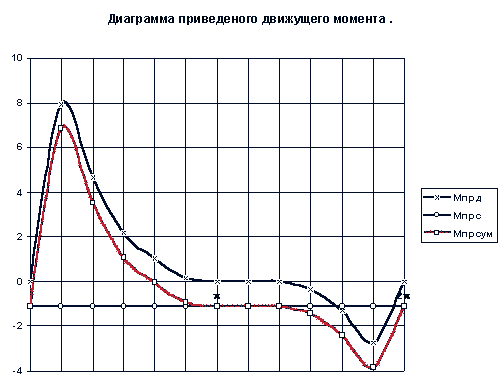
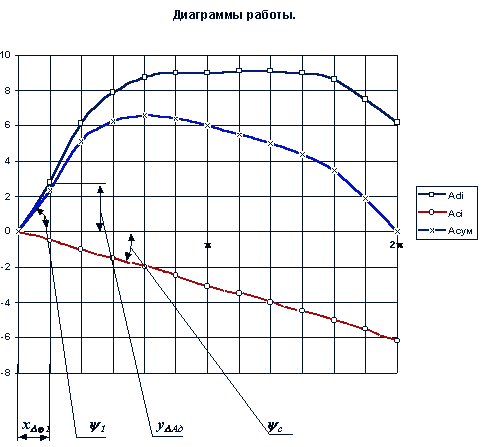
2. Построение диаграмм работы движущей силы, сил сопротивления и суммарной работы.
Диаграмму работы движущей силы получим интегрируя диаграмму ее приведенного момента
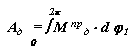
|
Интегрирование проведем графическим методом (рис.8.8), приняв при этом отрезок интегрирования равным k1 . Тогда масштаб полученной диаграммы работы движущей силы будет равен
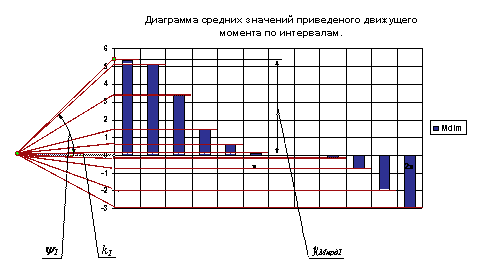
|
Рис. 8.8
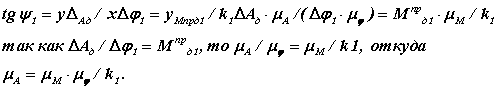
Величина среднеинтегрального момента сил сопротивления определяется по формуле
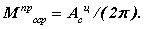
3. Построение диаграмм кинетических энергий.
Диаграммы кинетических энергий для первой и второй групп звеньев получает на основании теоремы об изменении кинетической энергии системы
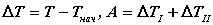
График кинетической энергии второй группы звеньев получим из зависимости
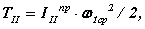
принимая, что w1 » w 1ср . Тогда диаграмма приведенного момента инерции второй группы звеньев в масштабе рассчитанном по формуле

соответствует диаграмме кинетической энергии ТII .
|
Рис. 8.9
График кинетической энергии первой группы звеньев приближенно строим по уравнению
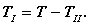
В каждом положении механизма из ординат кривой A= f (j 1) вычитаем ординаты yTII и получаем ординаты искомой диаграммы TI = f (j 1). Для этого необходимо ординаты диаграммы TII = f (j 1) из масштаба m T перевести в масштаб mA* по формуле

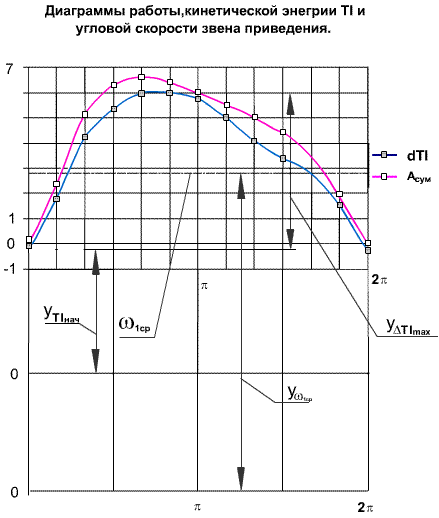
Диаграмма кинетической энергии первой группы звеньев представлена на рис. 8.10.
|
Рис. 8.10
4. Определение необходимого момента инерции маховых масс первой группы
Максимальное изменение кинетической энергии звеньев первой группы за цикл определяем по диаграмме
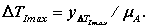
Тогда необходимый момент инерции маховых масс первой группы звеньев, обеспечивающий заданный коэффициент неравномерности, равен
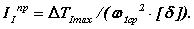
4.1. Определение момента инерции дополнительной маховой массы.
В нашем случае момент инерции дополнительной маховой массы рассчитывается по следующей зависимости
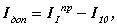
где I10 - момент инерции коленчатого вала .
5. Определение размеров маховика.
Принимаем конструктивное исполнение маховика - диск. Тогда его основные размеры и масса определятся по следующим зависимостям:
наружный диаметр
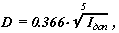
|
ширина b = y b * D ,
масса m = 1230* D 3,
где r = 7.8 кг/дм3 - плотность материала маховика ,
y b - коэффициент ширины .
7. Определение углового ускорения звена приведения.
Как отмечено ранее для расчета углового ускорения звена приведения e 1 = f(j 1) лучше пользоваться формулой :
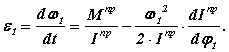
Необходимые для расчета значения величин определяем по ранее построенным диаграммам. Диаграмма функции e 1 = f(j 1 ) приведена на рис. 8.11.
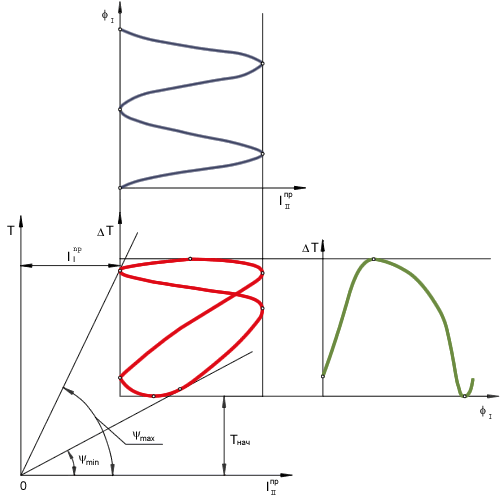
Расчет дополнительной маховой массы по методу Виттенбауэра.
Среди графо-аналитических методов расчета маховика теоретически точным считается метод Виттенбауэра. В основе этого метода лежит построение диаграммы кинетическая энергия - приведенный момент инерции (Рис.8.6). После построения этой диаграммы, рассчитываются минимальная w1min и максимальная w 1max угловые скорости, а по ним угловые коэффициенты наклона касательных
tgymax =m T * w 1max2 /(2 *m I ),
tgymin =m T * w 1min2 /(2 *m I ) .
Затем к диаграмме проводятся касательные, образующие с осью х углы ymax и ymin . Точка пересечения этих касательных образует начало новой системы координат, смещенное от исходной по оси y на
yI=m I*IпрI,
а по оси х на
xT = m T*Tнач ,
где IпрI - необходимый момент инерции звеньев первой группы, обеспечивающий заданный коэффициент неравномерности, Tнач - начальная кинетическая энергия системы. Так как точка пересечения касательных может при малых d выйти за пределы чертежа, величину ординаты yI можно рассчитать по отрезку ab, отсекаемому на оси у касательными:
yI=ab / (tgymax-tgymin).
|
Разработал ст.преподаватель кафедры «Прикладная механика» Годунов С.Ф.
Дата добавления: 2015-08-21; просмотров: 2797;
