Уравнение движения машины в дифференциальной форме.
Продифференцируем полученное выше уравнение по обобщенной координате
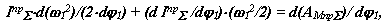
|
где
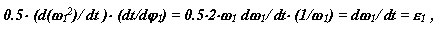
|
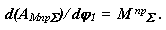
|
После подстановки получим
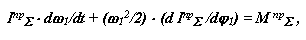
|
уравнение движения машины в дифференциальной форме.
Из этого уравнения после преобразований
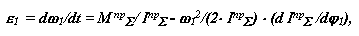
|
получим формулу для расчета углового ускорения звена приведения.
Для механических систем в которых приведенный момент не зависит от положения звеньев механизма.
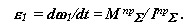
|
Определение параметров машины (приведение сил и масс).
Рассмотрим изображенную на рис. 6.1 механическую систему и ее динамическую модель. Запишем для них уравнение изменения кинетической энергии. Кинетическая энергия:
- для механической системы
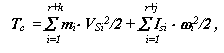
|
- для модели
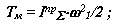
|
Суммарная работа внешних сил:
- для механической системы
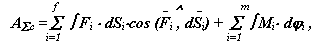
|
- для машины
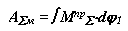
|
Модель будет энергетически эквивалентна рассматриваемой механической системе, если правые и левые части уравнений изменения кинетической энергии для модели и для системы будут соответственно равны. То есть для левых частей выполняется условие Тс = Тм , а для правых - Aå c = Aå м. Для того чтобы второе равенство выполнялось в течение всего диапазона изменения обобщенной координаты, необходимо обеспечить не равенство интегралов, а равенство подынтегральных выражений dAå c =dAå м. Подставляя в равенства, записанные ранее выражения для кинетических энергий и работ получим:
для левых частей
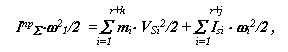
|
для правых частей
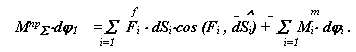
|
Из уравнения для левых частей получаем формулу для определения приведенного суммарного момента инерции машины
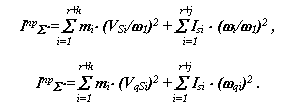
|
Из уравнения для правых частей получаем формулу для определения приведенного суммарного момента машины
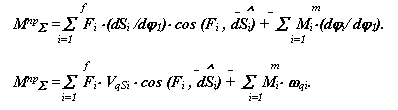
|
Механические характеристики машин.
Механической характеристикой машины называется зависимость силы или момента на выходном валу или рабочем органе машины от скорости или перемещения точки или звена ее приложения.
Рассмотрим примеры механических характеристик различных машин.
- Двигатели внутреннего сгорания (ДВС):
- четырехтактный ДВС
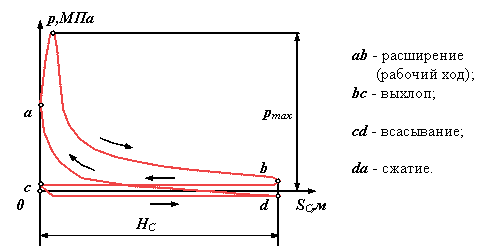
|
| Рис 6.2 |
o Индикаторная диаграмма - графическое изображение зависимости давления в цилиндре поршневой машины от хода поршня.
- двухтактный ДВС
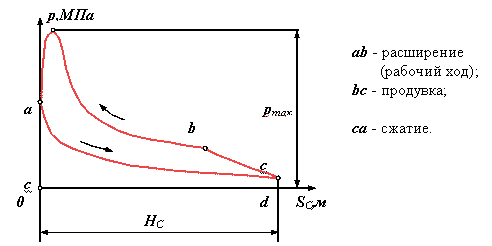
|
| Рис 6.3 |
- Электродвигатели
- асинхронный электродвигатель переменного тока На диаграмме: Мдп - пусковой момент; Мдн - номинальный крутящий момент; Мдк или Мдmax - критический или максимальный момент; wдн - номинальная круговая частота вращения вала двигателя; wдхх или wдс - частота вращения вала двигателя холостого хода или синхронная. Уравнение статической характеристики асинхронного электродвигателя на линеаризованном участке устойчивой части
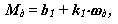
|
o где Мд - движущий момент на валу двигателя,
o wд - круговая частота вала двигателя ,
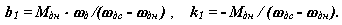
|
o Статическая характеристика асинхронного двигателя, выражающая зависимость нагрузки от скольжения, определяется формулой Клосса
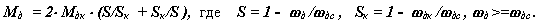
|
o

|
| Рис 6.4 |
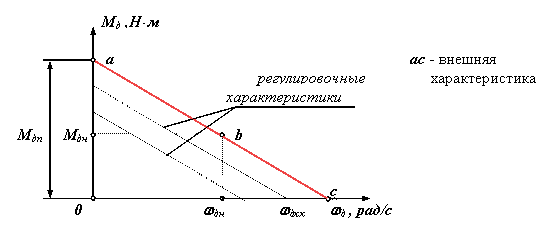
- двигатель постоянного тока с независимым возбуждением
|
| Рис 6.5 |
· Уравнение статической характеристики для двигателя постоянного тока с независимым возбуждением
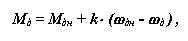
|
· где k = Мдн (wдхх - wдн ).
· В электрических параметрах характеристика записывается в следующем виде
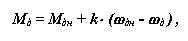
|
· где kM = Mдн/Iян - коэффициент момента, kw = (Uян - Rян × Iян ) / w дн - коэффициент противоэлектродвижущей силы, Uя - напряжение в цепи якоря, Rя - сопротивление цепи якоря
- Рабочие машины
- поршневой насос

|
- Рис 6.6
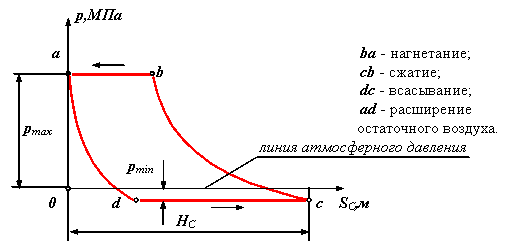
- поршневой компрессор
|
| Рис 6.7 |
o Линии bc и ad - линии сжатия и расширения газа (воздуха) определяются параметрами газа (объемом, давлением и температурой) и в общем виде описываются уравнением политропы p× Vn = const , где n - показатель политропы ( 1< n < 0 ).
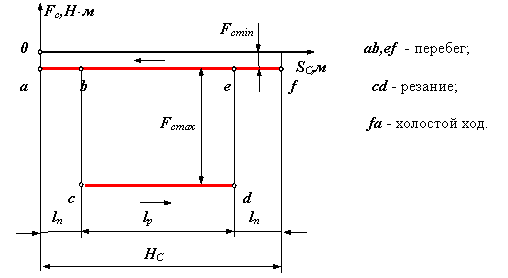
- строгальный станок
|
| Рис 6.8 |
o Механические характеристики определяют внешние силы и моменты, действующие на входные и выходные звенья, рассматриваемой механической системы со стороны взаимодействующих с ней внешних систем и окружающей среды. Характеристики определяются экспериментально, по результатам экспериментов получают регрессионные эмпирические модели, которые в дальнейшем используются при проведении динамических расчетов машин и механизмов.
Пример на определение параметров технологической машины(на приведение сил и масс ).
Дано: Кинематическая схема механизма поршневого насоса( li, j i ), Мд , Fc , mi , ISi ;
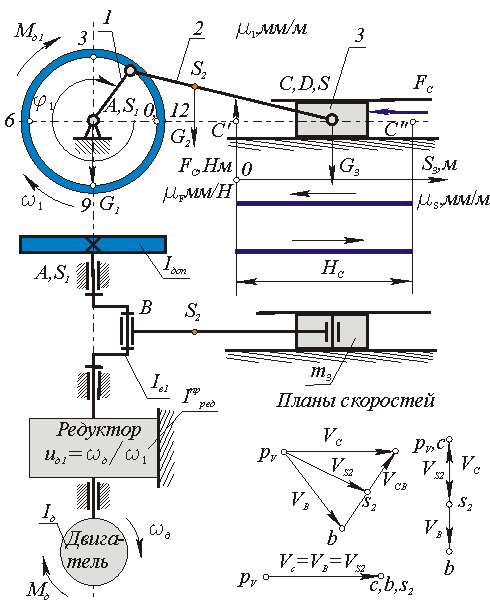
|
| Рис 6.8 |

|
| Рис 6.9 |
Определить: Мпрå , Iпрå =?
1. Определение сил веса Gi = mi ×g.
2.Определение кинематических передаточных функций.
Простой и наглядный метод определения передаточных функций - графоаналитический метод планов возможных скоростей. При этом в произвольном масштабе строятся планы скоростей для рада положений цикла движения механизма. По отрезкам плана скоростей рассчитываются соответствующие передаточные функции по следующим формулам ( для машины, схема которой изображена на рис.6.8 ):
Передаточные функции:
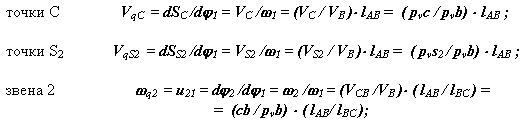
|
По этим формулам строятся цикловые диаграммы передаточных функций для рассматриваемого механизма ( см. рис. 6.10 ).
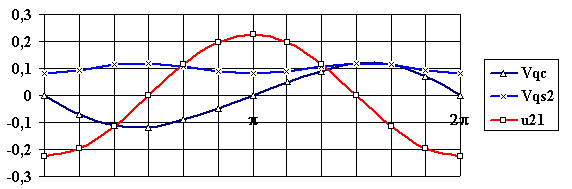
|
Рис. 6.10
3. Определение суммарного приведенного момента Мпрå
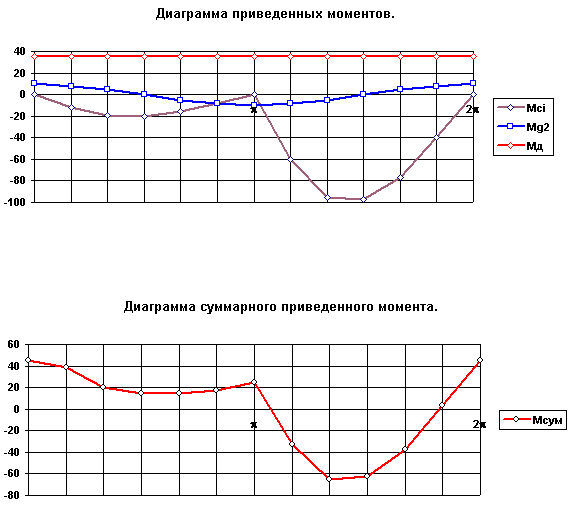
Для определения суммарного приведенного момента необходимо просуммировать приведенные моменты от всех внешних сил, действующих на рассматриваемую систему. Приведенный момент от силы равен скалярному произведению вектора силы на вектор передаточной функции точки ее приложения, от момента - произведению момента на передаточное отношение от звена приложения момента к звену приведения. На рассматриваемую систему действуют силы веса звеньев Gi , сила сопротивления Fс и движущий момент Мд . Приведенный момент от этих сил рассчитывается по формуле:
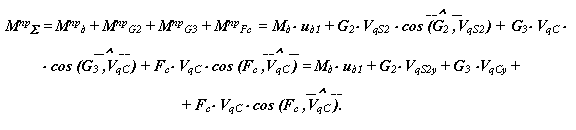
|
|
Рис. 6.11
4. Определение суммарного приведенного момента инерции Iпрå .
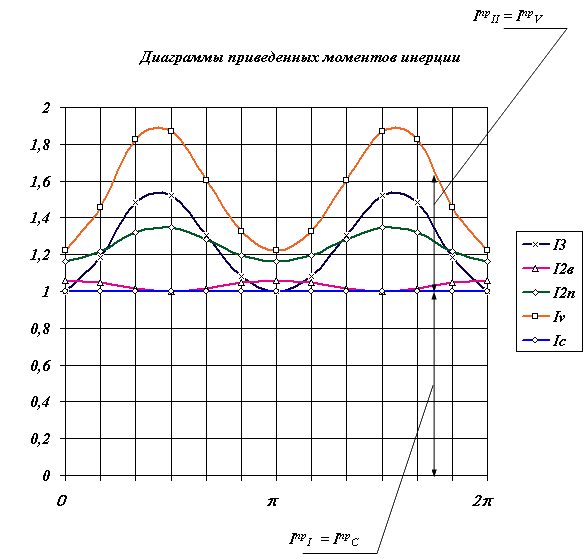
Для определения суммарного приведенного момента инерции необходимо просуммировать приведенные моменты инерции от всех масс и моментов инерции подвижных звеньев рассматриваемой системы. Приведенный момент инерции от массы равен произведению массы на квадрат передаточной функции ее центра, от момента инерции - произведению момента инерции звена на квадрат передаточного отношения от этого звена к звену приведения. Инерционность рассматриваемой системы определяется массами звеньев 2 и 3 и моментами инерции ротора двигателя, редуктора, коленчатого вала, маховика и звена 2. В суммарный приведенный момент инерции входят как составляющие не зависящие от положения механизма, так и составляющие, зависящие от обобщенной координаты. Первые имеют постоянный момент инерции и относятся к первой группе звеньев, момент инерции других - переменный, они образуют вторую группу. Приведенный момент для рассматриваемой системы определяется по формуле:
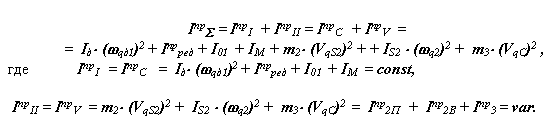
|
|
| Рис. 6.12 |
Таким образом выполнена поставленная задача - определены параметры динамической модели поршневого насоса: приведенный суммарный момент Мпрå и приведенный суммарный момент инерции Iпрå .
Лекция 7
Режимы движения машины.
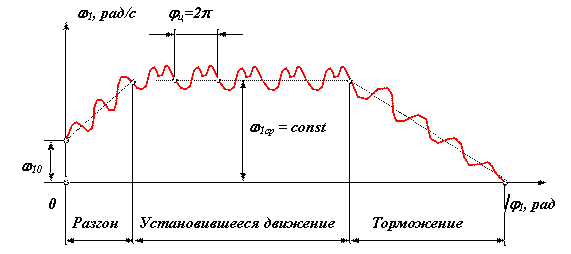
В зависимости от того какую работу совершают внешние силы за цикл движения машины различают три режима движения: разгон, торможение и установившееся движение. Циклом называют период времени или период изменения обобщенной координаты через который все параметры системы принимают первоначальные значения.
|
рис. 7.1
- Разгон => Адц > Асц , Аå ц > 0;
- Установившееся движение => Адц = Асц , Аå ц = 0;
- Торможение (выбег) => Адц< Асц , Аå ц < 0.
Режим движения "пуск - останов".
Существует большое количество машин и механизмов: гидроподъемники, манипуляторы, механизмы управления метательными аппаратами, механизмы шасси, механизмы автоматических дверей и многие другие, исполнительное звено которых перемещается из начального положения в конечное. При этом в начале и в конце цикла движения исполнительное звено неподвижно. Такой режим движения механизма называется режимом "пуск-останов". Механизм начинает движение из состояния покоя, в конце цикла выходное звено механизма должно остановиться и зафиксироваться в заданном положении. Возможны три варианта остановки выходного звена:
- остановка с жестким ударом (рис.7.2) w 1n > 0, e 1n стремиться к бесконечности ;
- остановка с мягким ударом (рис. 7.3 ) w 1n = 0, e 1n не равно 0 .
Для динамической модели в конечном положении
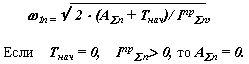
|
безударная остановка или остановка с удержанием в конечном положении (рис. 7.4) w 1n = 0, e 1n = 0 .
В этом случае к рассмотренному выше условию w 1n = 0 , добавляется условие e 1n = 0. Для динамической модели в конечном положении
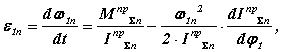
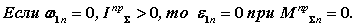
Таким образом при остановке с мягким ударом необходимо выполнить условие
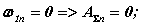
при безударной установке и фиксации объекта в конечном положении нужно выполнить одновременно два условия
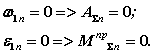
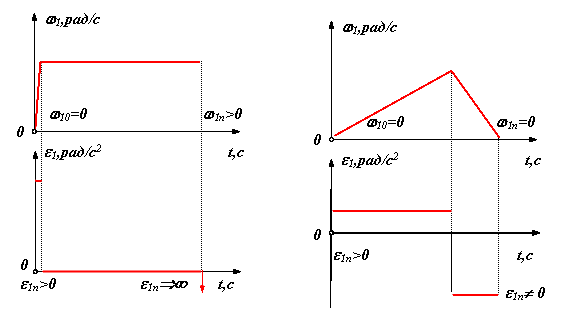
|
| рис. 7.2 | рис. 7.3 |
Дата добавления: 2015-08-21; просмотров: 1975;
