Матрица парных коэффициентов корреляции
| Y | X1 | X2 | X3 | X4 | X5 | |
| Y | ||||||
| X1 | 0,732705 | |||||
| X2 | 0,785156 | 0,706287 | ||||
| X3 | 0,179211 | -0,29849 | 0,208514 | |||
| X4 | 0,667343 | 0,924333 | 0,70069 | 0,299583 | ||
| X5 | 0,709204 | 0,940488 | 0,691809 | 0,326602 | 0,992945 |
В узлах матрицы находятся парные коэффициенты корреляции, характеризующие тесноту взаимосвязи между факторными признаками. Анализируя эти коэффициенты, отметим, что чем больше их абсолютная величина, тем большее влияние оказывает соответствующий факторный признак на результативный. Анализ полученной матрицы осуществляется в два этапа:
1. Если в первом столбце матрицы есть коэффициенты корреляции, для которых /r  / < 0,5, то соответствующие признаки из модели исключаются. В данном случае в первом столбце матрицы коэффициентов корреляции исключается фактор
/ < 0,5, то соответствующие признаки из модели исключаются. В данном случае в первом столбце матрицы коэффициентов корреляции исключается фактор 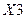 или коэффициент роста уровня инфляции. Данный фактор оказывает меньшее влияние на результативный признак, нежели оставшиеся четыре признака.
или коэффициент роста уровня инфляции. Данный фактор оказывает меньшее влияние на результативный признак, нежели оставшиеся четыре признака.
2. Анализируя парные коэффициенты корреляции факторных признаков друг с другом, (rXiXj), характеризующие тесноту их взаимосвязи, необходимо оценить их независимость друг от друга, поскольку это необходимое условие для дальнейшего проведения регрессионного анализа. В виду того, что в экономике абсолютно независимых признаков нет, необходимо выделить, по возможности, максимально независимые. Факторные признаки, находящиеся в тесной корреляционной зависимости друг с другом, называются мультиколлинеарными. Включение в модель мультиколлинеарных признаков делает невозможным экономическую интерпретацию регрессионной модели, так как изменение одного фактора влечет за собой изменение факторов с ним связанных, что может привести к «поломке» модели в целом.
Критерий мультиколлениарности факторов выглядит следующим образом:
/rXiXj/ > 0,8
В полученной матрице парных коэффициентов корреляции этому критерию отвечают два показателя, находящиеся на пересечении строк 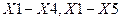 и
и 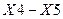 . Из каждой пары этих признаков в модели необходимо оставить один, он должен оказывать большее влияние на результативный признак. В итоге из модели исключаются факторы
. Из каждой пары этих признаков в модели необходимо оставить один, он должен оказывать большее влияние на результативный признак. В итоге из модели исключаются факторы 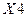 и
и 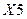 , т.е. коэффициент роста себестоимости реализованной продукции и коэффициент роста объёма её реализации.
, т.е. коэффициент роста себестоимости реализованной продукции и коэффициент роста объёма её реализации.
Итак, в регрессионную модель вводим факторы Х1 и Х2.
Далее осуществляется регрессионный анализ (сервис, анализ данных, регрессия). Вновь составляет таблица исходных данных с факторами Х1 и Х2. Регрессия в целом используется для анализа воздействия на отдельную зависимую переменную значений независимых переменных (факторов) и позволяет корреляционную связь между признаками представить в виде некоторой функциональной зависимости 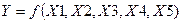 называемой уравнением регрессии или корреляционно-регрессионной моделью.
называемой уравнением регрессии или корреляционно-регрессионной моделью.
В результате регрессионного анализа получаем результаты расчета многомерной регрессии. Проанализируем полученные результаты.
Все коэффициенты регрессии значимы по критерию Стьюдента. Коэффициент множественной корреляции R составил 0,925, квадрат этой величины (коэффициент детерминации) означает, что вариация результативного признака в среднем на 85,5% объясняется за счет вариации факторных признаков, включенных в модель. Коэффициент детерминированности характеризует тесноту взаимосвязи между совокупностью факторных признаков и результативным показателем. Чем ближе значение R-квадрат к 1, тем теснее взаимосвязь. В нашем случае показатель, равный 0,855, указывает на правильный подбор факторов и на наличие взаимосвязи факторов с результативным показателем.
Рассматриваемая модель адекватна, поскольку расчетное значение F-критерия Фишера существенно превышает его табличное значение (Fнабл=52,401; Fтабл=1,53).
В качестве общего результата проведенного корреляционно-регрессионного анализа выступает множественное уравнение регрессии, которое имеет вид:
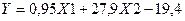
Полученное уравнение регрессии отвечает цели корреляционно-регрессионного анализа и является линейной моделью зависимости балансовой прибыли предприятия от двух факторов: коэффициента роста производительности труда и коэффициента имущества производственного назначения.
На основании полученной модели можно сделать вывод о том, что при увеличении уровня производительности труда на 1% к уровню предыдущего периода величина балансовой прибыли возрастет на 0,95 п.п.; увеличение же коэффициента имущества производственного назначения на 1% приведет к росту результативного показателя на 27,9 п.п. Слелдовательно, доминирующее влияние на рост балансовой прибыли оказывает увеличение стоимости имущества производственного назначения (обновление и рост основных средств предприятия).
По множественной регрессионной модели выполняется многофакторный прогноз результативного признака. Пусть известно, что Х1 = 3,0, а Х3 = 0,7. Подставим значения факторных признаков в модель, получим Упр = 0,95*3,0 + 27,9*0,7 – 19,4 = 2,98. Таким образом, при увеличении производительности труда и модернизации основных средств на предприятии балансовая прибыль в 1 квартале 2005 г. по отношению к предыдущему периоду (IV квартал 2004 г.) возрастет на 2,98%.
Так как при указанных значениях факторных признаков имеется фактическое значение результативного признака (среднее) (У = 3,17), можно найти ошибку прогноза по формуле:
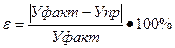 ,
,
где, Уфакт – фактическое значение результативного признака У;
Упр – прогнозное значение признака У.
Найдем ошибку прогноза в данном случае:
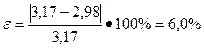 ,
,
Небольшая ошибка прогноза (не более 10%) говорит о том, что построенная множественная регрессионная модель хорошо отображает фактически сложившиеся взаимосвязи между исследуемыми показателями. Поэтому эту модель можно применять для прогеозирования результативного показателя (темпа роста балансовой прибыли).
Дата добавления: 2015-08-21; просмотров: 5882;
