Волновое уравнение, продольные, поперечные волны, скорости их распространения.стр233-240, 242-243

Уравнения движения связывают вторую пространственную производную напряжения со второй производной по времени от смещения частиц. Для однородной изотропной среды эта связь представлена в виде:

В общем случае в упругой среде независимо распространяются упругие колебания 2-х типов: в виде передачи деформаций первого рода – продольная сейсмическая волна Р(prima), и в виде передачи деформации второго рода – поперечная сейсмическая волна S(second). Продольные и поперечные волны распространяются по всему объему упругой среды, поэтому они называются объемными волнами. Продольная волна характеризуется безвихревым смещением частиц среды. Поперечная волна характеризуется отсутствием изменений объема. В жидких и газообразных средах поперечных волн не существует, т.к. отсутствие сцепления частиц не обеспечивает передачу сдвиговых деформаций. В отличие от продольных волн поперечные волны имеют свойство быть поляризованными в различных плоскостях. Если смещение частиц в процессе распространения волны происходит в одной плоскости , то такая волна называется линейно-поляризованной. Продольная волна всегда распространяется быстрее, чем поперечная в той же среде.

Скорости распространения соответственно равны

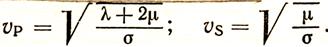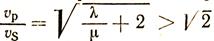Т.к. ,то продольные волны всегда распространяются с большей скоростью, чем поперечные.

Характер деформации элементов среды при прохождении поперечной волны

Характер деформации элементов среды при прохождении продольной волны