Связь между упругими напряжениями и деформациями.стр224-232

Под напряжением принимается равнодействующая сил, отнесенная к единице площади:

p=(∑Fi)/S

Единица измерения в СИ кг*м ^-1*с^-2

Абсолютно упругим телом называется такое, которое после прекращения действия приложенных к нему сил восстанавливает свою первоначальную форму и объем. Напряжения (силы, действующие на единицу площади), как и деформации, могут быть растягивающими или стягивающими, сдвиговыми или всесторонне сжимающими. Коэффициенты связи между напряжениями и деформациями среды называются модулями упругости. По закону Гука деформация растяжения (сжатия) в идеально упругих средах прямо пропорциональна напряжению. Уравнения связи для однородной изотропной среды:

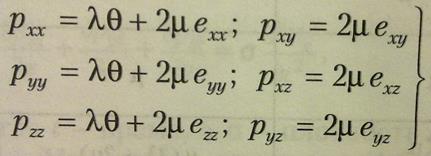
Коэффициенты пропорциональности λ и µ, называются упругими константами среды. Их можно выразить через модуль Юнга Е и коэф-т Пуассона v:

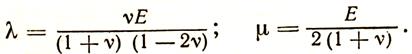
Модулем Юнга наз-ся коэф-т, который характеризует сопротивление ГП расширению или сжатию. Коэффициент Пуасона равен отношению относительного поперечного сужения (расширения) к относительному продольному удлинению (сжатию) грани. Коэффициент µ, называемый модулем сдвига, характеризует сопротивление горной породы изменению формы. Упругие модули связаны между собой 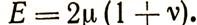Существует еще один модуль упругости - модуль всестороннего сжатия К=Е/3(1-2v). Коэффициент λ-коэффициент между нормальными напряжениями и деформациями сжатия-растяжения.