Оценка времени поддержания синхронизма в системе с автономным генератором (без принудительной подстройки).

Есть два генератора (на передаче и на приеме) с частотой f_ном и коэффициентом нестабильности 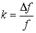Пусть в некоторый момент t₀ оба генератора начали работу в одинаковой фазе.

В следствие различия частот (или периодов), рассматриваемых генераторов, между ними появятся расхождения по фазе. С течением времени эти расхождения будут увеличиваться.

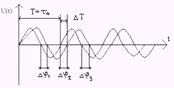
Задача. Определим время t_е, за которое уход по фазе относительно длительности единичного импульса составит Е, если нестабильность генераторов приема и передачи k

Под относительным уходом фазы будем понимать 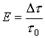– отношение интервала времени между идеальными и действительными ЗМ, отнесенное к длительности единичного интервала.

Если частоты генераторов равны f, а k одинаковы, то в худшем случае произойдет отклонение частот вследствие нестабильности в разные стороны.

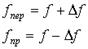Период 1-ого увеличивается на D T, второго уменьшается на D T.

Значит, за каждый период фазовый сдвиг будет возрастать на 2D T.

Зададимся некоторым абсолютным смещением значащих моментов по времени D t , ему будет соответствовать относительный уход фазы Е, причем, учитывая связь 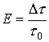, получим D t =Еt ₀

При этом количество периодов, за которое абсолютное смещение достигнет заданного равно 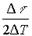, а время, за которое это произойдет равно

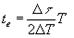. (**) Выражая D Т через k и Т, получим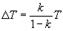

Учитывая, что в реальных системах k<<1, то 1-k @ 1.

Тогда D Т@ kT – подставим этот результат в (**), получим

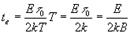
Используя полученное выражение можно найти требуемое k при заданных B, t_e и E.

Итак: при равных условиях время поддержания синхронизации зависит от скорости модуляции в канале! Невозможно долго сохранять синхронизацию без подстройки фазы.