Передаточные функции замкнутых систем

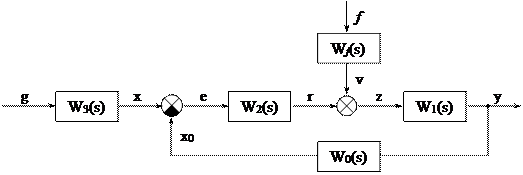Рассмотрим основной контур регулирования САУ следующего вида (будем использовать о.о.с.)

y = W₁(s)z = W₁(s)(r+v) = W₁(s)W₂(s)e + W_f(s)f = W_f(s)f + W₁(s)W₂(s)[W₃(s)g – W₀(s)y] =

= W_f(s)f + W₁(s)W₂(s)W₃(s)g - W₁(s)W₂(s)W₀(s)y.

.

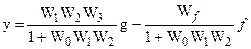После преобразований получим:

а) при f = 0

- ПФ замкнутой системы Ф_g по входному сигналу.

б) при g = 0

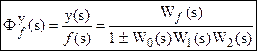- ПФ замкнутой системы Ф_f по возмущению.

"Обобщенное правило":

1) знаменатель равен 1±W(s), где

W(s) – произведение ПФ звеньев в замкнутом контуре регулирования.

2) числитель Ф_i равен произведению всех ПФ, находящихся на пути от входной координаты или возмущения до конечной координаты.

После такого преобразования можно построить упрощенную (приведенную) ПФ САУ:

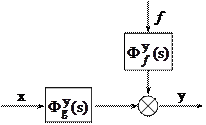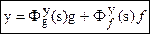
аналогично, используя "обобщенное правило" получим ПФ для ошибки е по входу g и возмущению f:

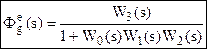
Замечание: 1) Здесь на пути между е и g находится W₃(s), а на пути между е и f три звена W_f, W₁ и W₀.

2) Знак "–" не учитывается, т.к. он входит в итоге в уравнение.

Пример 1. Дана структурная схема ЭД п.т.н.в. (ее можно получить из системы 4^х уравнений, приводимых ранее в теме "ПФ")

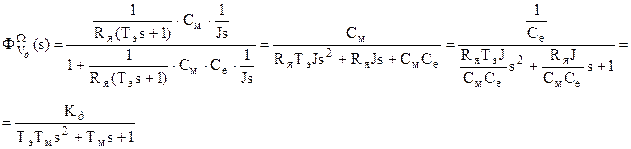
Вывод: Если бы мы знали это "обобщенное правило" ранее, то мы бы значительно быстрее вывели передаточную функцию ЭД п.т.н.в.

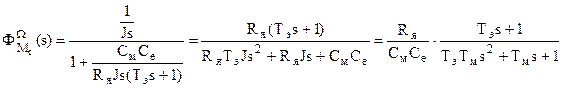
Получены правильные результаты. Это подтверждает "обобщенное правило" получения ПФ замкнутых САУ.

Примечание: Если необходимо получить ПФ ЭД для α, то

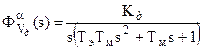→ как для последовательного соединения.

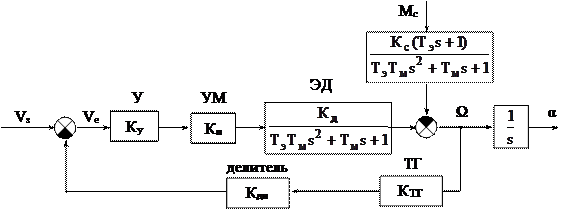Пример 2. Получить уравнение и ПФ для ошибки для САУ стабилизации скорости ЭД п.т.н.в.

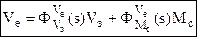→ общее уравнение ошибки,

где

;

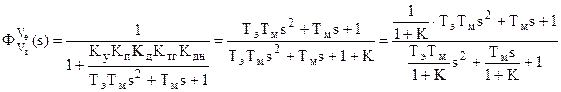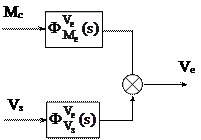
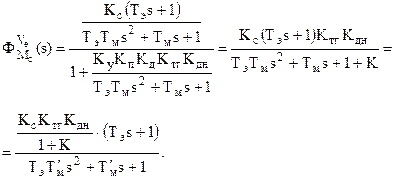
Используя эти ПФ можно получить дифференциальное уравнение для САУ ЭП → таким образом получаются дифференциальные уравнения систем (особенно высокого порядка).

Дополнение:

В установившемся режиме при V_з = const (статический режим) можно получить уравнение ошибки, учитывая, что sⁱ = 0 (производные = 0)

.

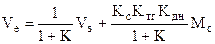Передаточная функция разомкнутой системы и характеристическое уравнение

Особую роль в исследовании САУ играет знаменатель ПФ замкнутых систем:

1 + W(s) ,

здесь W(s) – называют ПФ разомкнутой системы, т.к. мысленно контур разрывают и получается вход и выход.

Если выражение 1+W(s) приравнять нулю, то получится так называемое характеристическое уравнение

1 + W(s) , или при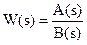

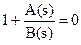→ А(s) + B(s) = 0 – характеристическое уравнение.

Вывод: 1. Для получение характеристического уравнения необходимо сложить числитель и знаменатель ПФ разомкнутой системы и приравнять его нулю.

2. По существу – это левая часть дифференциального уравнения, которое описывает САУ.

3. По нему можно определить корни (и др. характеристики) системы, т.е. движение системы, таким образом, характеристическое уравнение очень важное соотношение в теории управления.

Передаточная функция разомкнутой системы также очень важна для проектирования и исследования систем – по ней строят ЛАЧХ и осуществляют синтез и определяют устойчивость системы.