Комплексная обработка при качественной интерпретации

Приемы комплексной интерпретации для качественного истолкования геологиче- ских и геофизических данных разработаны достаточно хорошо. При этом основными задачами являются: районирование территории по комплексу данных; выделение ме- стоположения аномалий и аномальных участков; объяснение их геологической приро- ды. Обычно используют приемы визуального анализа полей и формализованные про- цедуры, допускающие использование ЭВМ. Основной принцип качественного истол- кования геофизических данных — принцип аналогии — состоит из обучения на эта- лонном участке с известным строением и анализа аналогичного по строению, но неизу- ченного участка. При этом широко используют приемы распознавания образов.

Признаки полей. При качественной интерпретации основными понятиями явля- ются признаки полей. Признаком называют чаще количественный, реже качественный, но кодированный показатель поведения поля в данной точке. Количественный при- знак—амплитуда геофизического поля, качественный — например, знак поля: положи- тельным значением поля соответствует код +1, отрицательным — код —1, а близким к нулю— код 0. Такой качественный признак, как сложность геологического строения, оцениваемый по карте, может быть закодирован, например, кодом 0 — простое строе- ние, 1 — сложное; 2 — очень сложное строение.

Этот признак можно определить полуколичественно, если разделить геологиче- скую карту на клетки размером, например, 2х2 см и подсчитать число геологических комплексов, попадающих на каждую из них или, как принято говорить, в «окно». Од- нородная толща получит значение признака 0, геологический контакт в пределах «ок- на» даст код 1, сочленение трех комплексов получит код 2. В таком скользящем по кар- те «окне» можно подсчитать интенсивность проявления магматизма, разломной текто- ники, направленность разломов и т.п.

Различают признаки первичные, например, амплитуда геофизического поля, не- посредственно измеренная в определенной точке, и вторичные (рассчитываемые по первичным), например, среднее значение поля в «окне», простирание изолиний, дис- персия поля или просто разница максимального и минимального значений поля в «ок- не». Полезными вторичными признаками являются коэффициенты линейной корреля- ции rху двух геофизических полей Х и У, рассчитанные в скользящем «окне» по форму- ле

én ù

(8.5)

ëi =1 û

n n

где

X =åX i n, X

i =1

å(X i

i =1

- X )2 / n ;

формулы для Y и σY аналогичны. Физический смысл коэффициента корреляции сводит- ся к оценке связей между полями. Коэффициент корреляции rxy может принимать зна- чения от —1 до 1. Значения коэффициента корреляции 0,7 < rxy < 1 говорят о том, что связи между полями не случайны и на данном участке скорее всего обусловлены одним общим источником (процессом или объектом). Отсутствие корреляции (rxy ≈ 0) говорит о том, что изменения полей вызваны разными и независимыми причинами. Например, массивное рудное тело увеличивает значения ηк и понижает значения ρк, измеренные над ним на поверхности земли, тогда как вкрапленные руды, увеличивая ηк, практиче- ски не изменяют ρк, и коэффициенты корреляции в этих двух случаях будут, естествен- но, различаться. Высокие диагностические качества на рудоперспективных площадях проявляет коэффициент корреляции магнитного поля и ВП, позволяя выделять рудные аномалии и зоны гидротермально-метасоматического происхождения.

Расчет вторичных признаков позволяет намного увеличить общее число призна- ков для последующей оценки их эффективности и выбора наиболее информативных из них. Большое число признаков вручную изучить трудно, поэтому такие приемы пред- полагают широкое использование ЭВМ.

Функция комплексного показателя. Для визуального анализа информации необ- ходимо из многих признаков получить один результат, надежно выделяющий интере- сующий объект. Наиболее просто этот процесс можно показать на примере расчета функции комплексного показателя (ФКП), предложенной Г.С. Вахромеевым. Расчет ФКП основан на суммировании признаков геофизических полей, осуществляемом та- ким образом, чтобы максимально усилить полезный эффект от искомого объекта. На- пример, для ФГМ рудного объекта (см. рис. 8.2) характерны повышенные значения Δg, ΔZ и ηк и пониженные значения UЕП и ρк. Чтобы усилить эффект всех этих полей, надо взять первые три признака со знаком «плюс», а два вторых — со знаком «минус». Для сложения разных полей используемые параметры необходимо сначала перевести в единую безразмерную форму путем их пересчета в коэффициенты контрастности γk i , [см. формулу (8.3)], где k — номер признака или метода; i — номер точки наблюдения. Тогда ФКП можно вычислить с помощью весового суммирования:

q= C g -

k =1

N

å Ck gk i , (8.6)

k = M +1

где знаки «плюс» и «минус» выбраны так, как указывалось выше («плюс» для Δg, ΔZ и

ηк и «минус» для UЕП и ρк).

Весовые коэффициенты Ck оценивают следующим образом. Сначала на основе интуиции или опыта назначают некоторые априорные весовые коэффициенты. Напри- мер, после расчета у оказалось, что UЕП дает большую по амплитуде аномалию, чем ρк, значит, можно взять CЕП = 2, а Cρ = 1. Аналогично выбирают, например, Cη = 2, a

N

k =1

будет иметь единичную дисперсию, и значения θ > 3 можно рассматривать как досто-

верные аномалии, а θ = 1—3 считать слабыми аномалиями.

Если изменяется задача поиска, то изменяется и набор признаков и их весовые ко- эффициенты. Например, для поисков вкрапленных руд наибольший весовой коэффици- ент должен быть у метода ВП.

эталоны. На них по каждому из анализирован- ных признаков геофизических полей строят гистограммы распределения и оценивают сте- пень разделения гистограмм для рудного и без- рудного участков или информативность при- знаков.

Если для одного из признаков гистограм- мы полностью разделились, то задача может быть решена по этому одному признаку. Такие случаи встречаются редко. Как правило, гисто- граммы частично пересекаются, т.е. надеж- ность разделения объектов по каждому из при- знаков недостаточна. Выбрав два признака Х и Y с наибольшим разделением гистограмм,

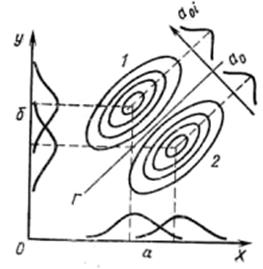
Рис. 8.5. Разделение аномалий на руд- ный (1) и безрудный (2) клас- сы по двум признакам Х и Y.

а — разделение только по X; 6 — разделе- ние только по Y; Г — линия границы наи- лучшего разделения по Х и Y

можно изобразить их на плоскости XOY в виде полей точек для рудного и безрудного участ- ков (рис. 8.5). Проекции этих полей точек на оси Х и Y дают исходные гистограммы по ка- ждому признаку для участков 1 и 2, которые полностью не разделяются (случаи а и б). Но по двум признакам на комплексной плоскости

XOY облака точек для участков 1 и 2 в центре рис. 8.5 удается разделить линией Г,

уравнение которой

Y = a0 – a1X . (8.7)

Эта линия или граница позволяет решить задачу об отнесении объектов к рудно-

му или безрудному классу. Если сочетание признаков Х и Y для проверяемой аномалии

дает точку выше границы, то объект рудный, а если ниже — безрудный. Вычислением коэффициентов a0 и а1 заканчивается этап обучения.

На этапе анализа для всех проверяемых аномалий по значениям признаков Х и Y положение точки относительно линии либо определяют графически, либо рассчитыва- ют величину a0 i =Yi – аiХi, которую сравнивают с a0 из формулы (8.7). Очевидно, что при a0 i > a0 (эталонного) точка окажется выше границы, т.е. будет отнесена к рудному классу, а при a0 i < a0 окажется ниже границы и будет отнесена к безрудному классу.

При использовании большего числа признаков ситуацию трудно изобразить гра- фически, но ЭВМ и в таком многомерном пространстве на этапе обучения найдет не- кую гиперплоскость, разделяющую точки классов 1 и 2. Затем, на этапе анализа, урав- нение этой гиперплоскости используют для разбраковки аномалий на два класса.

Разделение полей для целей геокартирования. При решении задачи геокартиро- вания по комплексу признаков возникает необходимость разделения полей не на два, а на большее число классов, соизмеримое с числом различных геологических комплек- сов на территории съемки. Алгоритм распознавания образов при этом также работает в два этапа: обучения на эталонах и распознавания. В период обучения каждый геологи- ческий комплекс характеризуется своим облаком точек в многомерном пространстве признаков, причем облака для разных комплексов, если не разделяются достаточно на- дежно, подлежат объединению. Для каждого облака оценивают координаты центра (средние значения признаков) и радиус (дисперсию). Совокупность признаков для каж- дой точки наблюдения дает некоторую точку в многомерном пространстве признаков. Алгоритм распознавания оценивает, к какому облаку-эталону можно отнести эту точку (т.е. к породам какого класса). Если точка не может быть уверенно отнесена ни к одно- му эталонному классу, то она не подлежит классификации.

Подобный алгоритм требует довольно большого объема вычислений даже с ис- пользованием современных ЭВМ. Его работу можно сделать более производительной и надежной, если сначала разделить площадь по комплексу признаков на кусочно- однородные участки. В их пределах средние значения и дисперсия поля сохраняются постоянными, но зато заметно изменяются на границах участков. Далее для каждого такого однородного участка по средним значениям и дисперсии полей проводят опо- знавание геологической принадлежности этих участков путем сопоставления с этало- нами, как описано выше. Использование вместо отдельных точек целых участков за- метно повышает надежность распознавания, так как признаки, участвующие в распо- знавании, становятся более устойчивыми.

Принципы работы алгоритмов распознавания образов описаны в самых общих чертах. На практике применяют несколько десятков алгоритмов распознавания, осно- ванных на рассмотренных или несколько иных принципах. Несильно различаясь по су- ти, они весьма разнообразны в деталях работы и, как правило, значительно сложнее из- ложенной выше принципиальной схемы.