Прямые и обратные задачи магниторазведки

Прямая задача магниторазведки состоит в определении параметров магнитного поля (вычислении магнитных аномалий) по известным характеристикам магнитных масс: формы, размеров, глубины залегания, углов намагничения и магнитной воспри- имчивости. Обратная задача магниторазведки представляет собой количественный рас- чет параметров (форма, размеры, глубина залегания и др.) магнитных масс по заданно- му на профиле или площади распределению значений одного или нескольких элемен- тов магнитного поля Земли.

Принципы, решения прямой задачи магниторазведки. Прямую задачу магнито- разведки решают с помощью закона Кулона: F = m1·m2 /μr2, где m1,m2 —взаимодейст- вующие с силой F массы, центры которых расположены на расстоянии r; μ— магнит- ная проницаемость вмещающей среды. Так как практически все горные породы, за ис- ключением ферромагнитных железных руд, имеют μ = μ0, то в теории магниторазведки этот параметр считают постоянным и μ0 = 4π 10-7 Гн/м. Магнитных масс как самостоя- тельных субстанций в природе не существует, а магнитные свойства тел являются

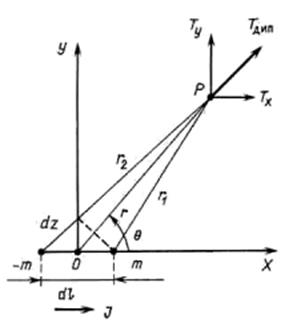
Рис.3.2 Магнитный диполь

следствием движения электрически заря- женных частиц в атомах вещества. Тем не менее, в теории магнетизма продолжают использовать закон Кулона, понимая под магнитной массой произведение интен- сивности намагничения I на площадь s намагниченного тела, перпендикулярную к вектору I: m=Is. Для облегчения реше- ния прямых задач в теорию магнетизма вводят по закону Кулона понятие магнит- ного потенциала точечной магнитной массы

UT = m/μr, FT = - ∂U/∂r. (3.7)

Так как намагниченные тела — это совокупности неразделяемых положи- тельных и отрицательных масс, то в тео- рию магнетизма вводят понятие магнит- ного диполя, т. е. совокупности двух рав- ных, близко (на расстоянии dl) располо- женных магнитных масс противополож-

ных знаков (± т). Потенциал диполя dU легко получить, используя рис. 3.2 и считая,

что длина диполя dl много меньше расстояний r, r1, r2 до точек наблюдений,

æ ö

dU =m ç1 -1 ÷=m ×dr

»m dl cosq

=dM cosq

=IdV cosq

(3.8)

mèr1

r2ø

m r1r2

m r 2

m r 2

m r 2

где dM = mdl = Idsdl = IdV — магнитный момент диполя; I — интенсивность намагничения диполя, направленная вдоль его оси; dl — длина; ds — площадь попе- речного сечения; dV = dlds -— элементарный объем; θ — угол между осью диполя и радиусом r, близкий (при dl << r) к углам между диполями r1 и r2. Из формулы (3.8) можно получить выражения для компонент напряженности магнитного поля диполя в плоскости (x, О, y):

Tx = ∂(dU)/ ∂x = dM(2x2-y2)/(x2+y2)5/2 μ ; Ty = ∂(dU)/ ∂y = dM 3xy/(x2+y2)5/2 μ

При замене x2+y2 = r2 и x/r = cos θ выражение для полного вектора напряженно-

сти магнитного поля диполя получает вид

dT =

T2 +T 2 =dM

1+3cos2 q

.

(3.9)

x y r3 m

На оси диполя (θ = 0) и перпендикуляра к его центру, т. е. на экваторе (θ = 90°),

получаем напряженности

T0 = 2dM/μr3, TЭ = dM/μr3. (3.10)

Поскольку реальные намагниченные тела можно рассматривать как совокупность элементарных магнитных диполей с учетом свойства суперпозиции потенциалы и ано- мальные значения напряженности любого намагниченного тела при использовании вы- ражений (3.7)—(3.9) можно записать следующим образом:

UV =

òòò

I cosqdV ,

mr2

TV =

I

òòò

1+3cos2 q

dV

mr3

(3.11)

V V

где интегрирование ведут по всему объему тела V. Уравнения (3.11) являются ос- новными в теории магниторазведки. Аналитические выражения с помощью (3.11) по- лучают лишь для тел простой геометрической формы и однородной (постоянной) на- магниченности. Для тел более сложной формы и, особенно, при переменной намагни- ченности возможны лишь численные приближенные решения, получаемые с помощью ЭВМ. Анализ решений прямой задачи служит основой для решения обратной задачи.

Рассмотрим решение прямой и обратной задач для некоторых простых тел: вер- тикального бесконечного стержня, шара, вертикального пласта и горизонтального ци- линдра бесконечного простирания при их вертикальной и однородной намагниченно- сти (вектор I постоянен внутри тела). Допущение вертикальной намагниченности не только упрощает решение задач, но и является вполне обоснованным, поскольку ин- дукционная намагниченность горных пород при широте, большей 50—60°, т. е. для большей части территории страны, близка к вертикальной.