Обобщенный метод линии положения

Навигационный параметр. Место самолета можно определить с помощью различных технических, в том числе радионавигационных. средств и разными методами. Но как показал профессор В.В.Каврайский, практически все эти способы можно рассматривать как частные случаи обобщенного метода линий положения. Это не какой-то конкретный способ определения МС, а абстрактный теоретический подход, некая схема, выражающая то общее, что содержится в любом способе местоопределения. Понимание обобщенного метода линий положения позволяет легко осваивать любые конкретные способы определения МС, независимо от того, на каких конкретных технических средствах они основаны, а также позволяет с единых позиций, унифицированными методами оценивать точность применяемых методов.

Основными понятиями, на которых основан этот метод, являются понятия навигационного параметра и линии положения.

В полете с помощью приборов можно измерить самые разные величины: пеленги, дальности, путевую скорость , угол сноса, температуру воздуха и т.д. В широком смысле слова их можно назвать навигационными параметрами, потому что эти величины используются для навигации.

Но в узком смысле, с точки зрения обобщенного метода линий положения, под навигационными параметрами понимаются не любые величины, применяемые в навигации, а только те, значения которых жестко связаны с точкой в пространстве, в которой производится их измерение.

Навигационный параметр - это физическая или геометрическая величина, значение которой функционально связано с данной точкой пространства.

Напомним понятие функции, широко используемое в математике. Если говорят, что y является функцией x, то это означает, что каждому значению x соответствует определенное значение y, то есть, что эти величины жестко взаимосвязаны. Неважно, каким образом задана эта связь. В математике она наиболее часто выражается формулой, по которой можно рассчитать y при любом заданном x. Но эта связь может быть задана и любым другим способом: графиком функции, таблицей… Неважно, каким образом она задана, главное, что она существует.

В приведенном определении навигационного параметра говорится, что его значение является функцией не величины (числа), а точки в пространстве. Это означает, что за каждой точкой «закреплено» определенное значение этой величины (навигационного параметра). Следовательно, для того, чтобы решить, является ли какая-либо измеренная величина навигационным параметром (в узком смысле, с точки зрения обобщенного метода линий положения), необходимо только выяснить, является ли ее значение вполне определенным в данной точке, либо может быть в этой точке различным, то есть с данной точкой жестко не связано.

Приведем примеры некоторых величин, и рассмотрим, являются ли они навигационными параметрами.

1) Наклонная дальность до радиостанции. Наклонная дальность – это расстояние от какой-то конкретной радиостанции до данной точки (например, до ВС) по прямой. Если ВС в данный момент времени находится в какой-то точке пространства, то конечно, его расстояние до радиостанции (наклонная дальность) является вполне определенной величиной, например, 137 км, а не 100 км, не 64 км и т.п. Следовательно, наклонная дальность – это навигационный параметр, являющийся в данном случае геометрической величиной.

2) Атмосферное давление. В любой момент времени в каждой точке околоземного пространства имеется вполне определенное значение атмосферного давления, например, 756 мм рт.ст или любое другое. Следовательно, атмосферное давление тоже является навигационным параметром, это физическая величина.

Не имеет значения, что атмосферное давление непрерывно меняется во времени и уже через минуту его значение в этой же точке, может быть, будет уже другим. Здесь важно, что в любой данный момент оно имеет вполне определенное значение.

3) Путевая скорость, то есть скорость перемещения ВС относительно Земли. Конечно, эта величина широко используется в навигации, но ее можно назвать навигационным параметром только в широком смысле слова, но не с точки зрения метода линий положения, поскольку она не попадает под приведенное определение. Действительно, разве можно сказать, что за данной точкой пространство закреплено какое-то определенное значение путевой скорости. Конечно, нет. Во-первых. если в данной точке сейчас не находится ВС, то путевой скорости в этой точке вообще не существует. Во-вторых, даже если через точку пролетает ВС, то очевидно, что его путевая скорость может быть различной и будет зависеть от истинной воздушной скорости ВС, от курса ВС, от скорости и направления ветра в данной точке. Следовательно, за самой точкой не закреплено никакое конкретное значение путевой скорости, поэтому она не является навигационным параметром.

4) Магнитное склонение. Магнитное склонение – это угол между северными направлениями истинного и магнитного меридианов. В любой точке однозначно определено направление на северный географический полюс (северное направление истинного меридиана) и однозначно определено направление горизонтальной составляющей вектора напряженности магнитного поля Земли (северное направление магнитного меридиана). Следовательно, в каждой точке имеется вполне определенный угол между этими направлениями ( магнитное склонение). Поэтому ΔМ – это навигационный параметр.

Разумеется, можно привести множество примеров величин, которые в соответствии с приведенным определением являются навигационными параметрами. Но в навигации используются только те из них, которые реально могут быть измерены в полете, то есть те, для измерения которых на борту действительно имеются соответствующие приборы. Например, магнитное склонение в принципе является навигационным параметром, но на самолете нет оборудования, которое позволило бы его непосредственно измерить, поэтому ΔМ как навигационный параметр не используется для определения МС (по крайней мере пока). Разумеется, это не отменяет возможность использования ΔМ для решения разных навигационных задач, в том числе, для вычисления значений других навигационных параметров (например, истинного пеленга самолета).

Поверхность и линия положения. Поскольку значение навигационного параметра зависит от того, где в данный момент времени находится ВС, появляется возможность использовать его измеренное в полете значение для определения МС. Действительно, если бортовые приборы показывают, что в данный момент навигационный параметр имеет такое-то вполне определенное численное значение, то это означает что ВС сейчас находится не где угодно, а может находиться только в одной из множества тех точек пространства, в которых значение параметра именно такое. Если, путешествуя пешком по стране и заблудившись, Вы обнаружили, что у вас под ногами асфальт (да еще с с нанесенной на него дорожной разметкой), то это означает, что вы находитесь не в поле, не в лесу, не в болоте, а на какой-то дороге. На какой именно дороге и в каком ее месте Вы, конечно, не знаете, но множество точек на карте, в которых вы в принципе могли бы находиться, существенно уменьшилось. В этом примере роль навигационного параметра играет вид подстилающей поверхности.

Если в какой-то точке пространства навигационный параметр имеет какое-то определенное значение, то это не вовсе не значит, что в других точках его значения должны быть обязательно другие. Наверняка, точно такое же значение параметр имеет и во многих других точках. Например, точки, в которых наклонная дальность равна 100 км находятся и к северу, и к востоку от радиостанции, вообще в любом направлении. Таких точек бесконечно многого. Но, как правило, точки с одинаковым численным значением навигационного параметра выстраиваются в пространстве, образуя некоторую поверхность.

Поверхность положения – геометрическое место точек в пространстве с одинаковым значением навигационного параметра (рис. 2.10).

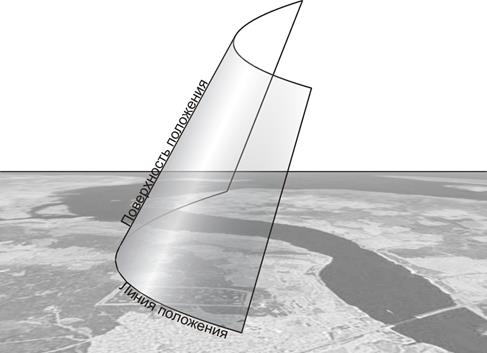
Рис. 2.10. Поверхность и линия положения

Обычно для каждого вида навигационного параметра поверхность положения имеет свою определенную форму. Для параметра наклонная дальность поверхность положения имеет форму сферы с центром в точке расположения радиостанции (рис. 2.11).

Рис. 2.11. Поверхность положения для навигационного параметра наклонная дальность

Ведь сфера и есть геометрическое место точек, одинаково удаленных от некоторой точки, называемой центром сферы. Поэтому, если в полете измерено, что наклонная дальность до радиомаяка составляет 237 км, то это означает, что ВС сейчас расположено в одной из точек сферы радиусом 237 км с центром в точке расположения радиомаяка. Поэтому поверхность и называется поверхностью положения. ВС не может находиться ни внутри, ни снаружи этой сферы, потому что тогда значение параметра (дальности) было бы другим.

Каждому численному значению навигационного параметра соответствует своя поверхность положения, поэтому для каждого вида навигационного параметра существует целое семейство поверхностей положения, отличающихся значением параметра. Так, для параметра наклонная дальность это семейство представляет собой бесконечное множество сфер разного радиуса с общим центром в точке расположения радиомаяка. И когда в полете при измерении наклонной дальности бортовыми приборами определяется численное значение этой дальности, то и становится ясным, на какой именно из этого множества сфер (поверхностей положения) в данный момент находится ВС.

Поверхность положения может пересекаться с земной поверхностью. При пересечении этих поверхностей образуется линия, в каждой точке которой, конечно, такое же значение параметра, как и на всей поверхности положения. Эта линия называется линией положения.

Линия положения – геометрическое место точек на земной поверхности с одинаковым значением навигационного параметра.

Если навигационный параметр является геометрической величиной, то обычно каждому его виду соответствует своя геометрическая форма линии положения (окружность, ортодромия, гипербола и т.д.). Изменяя значение навигационного параметра можно получить целое семейство линий положения, каждая из которых соответствует своему значению параметра.

Определение места самолета. Если в полете с помощью приборов измерить значение навигационного параметра в точке нахождения ВС и построить на карте линию положения, соответствующую этому значению параметра, то очевидно, что МС может находиться только в одной из точек этой линии. Ведь только на ней значение параметра именно такое, какое было измерено. Но в какой именно точке этой линии находится ВС, конечно, неизвестно. Однако можно измерить какой-либо другой параметр и также проложить на карте соответствующую ему линию положения. Поскольку ВС находится одновременно и на первой, и на второй линии положения, то очевидно, что оно находится в точке их пересечения. Собственно в этом и заключается идея обобщенного метода линий положения (рис. 2.12).

В традиционной навигации линии положения действительно прокладывают на карте, и место самолета получают графическим путем. Но в принципе это не обязательно. Ведь каждая линия положения описывается определенным уравнением в географической системе координат. Если в уравнения, описывающие две линии положения, подставить численные значения измеренных параметров, то получится система из двух уравнений, неизвестными в которой будут являться координаты точки, в которой измерены эти параметры. А это и есть широта и долгота самолета. Таким образом, решив эту систему уравнений, можно определить место самолета.

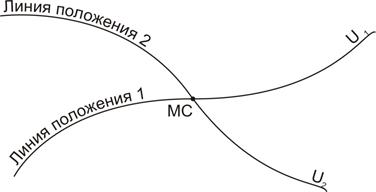
Рис.2.12. Определение места самолета по двум линиям положения

К сожалению, из-за сферичности Земли эти уравнения имеют достаточно сложный вид и решить их в полете «вручную» вряд ли возможно. Однако, при наличии на борту навигационного вычислителя (компьютера), входящего в состав пилотажно-навигационного комплекса, это вполне возможно. Например, в полете непрерывно измеряются дальности до двух радиомаяков, которые поступают в вычислитель. В памяти вычислителя хранятся географические координаты этих радиомаяков. По запрограммированным алгоритмам вычислитель непрерывно решает численными методами упомянутую систему из двух уравнений и выдает экипажу текущие значения широты и долготы самолета. В данном случае никакие линии положения на карте, конечно, не строятся. Задача решается аналитическим путем, по формулам. Но суть от этого не меняется. Это также реализация обобщенного метода линий положения.