Понятие о точности навигационных измерений

Необходимость учета точности измерений. Навигация была бы совсем простым делом, если бы не три фактора, которые все усложняют.

Во-первых, Земля не плоская, а круглая (а на самом деле имеет еще более сложную форму). Это вызывает необходимость учета при навигационных вычислениях и измерениях углов схождения меридианов, азимутальных поправок и пр. А при использовании аэронавигационных карт необходимо знать и учитывать искажения на картах. Пути решения возникающих при этом проблем рассматриваются в курсах «Геоинформационные основы навигации» или «Авиационная картография».

Во-вторых, влияние ветра на полет ВС. Это вызывает необходимость определения и учета угла сноса, расчета путевой скорости и т.п. Решение этих задач рассматривается в традиционных курсах «Аэронавигации» («Воздушной навигации»).

В-третьих, современная навигация выполняется в основном не визуально, а по приборам, которые предназначены для измерения различных навигационных параметров. Но ни один прибор (не только навигационный) никогда не измерит абсолютно точное значение величины. Всегда будет присутствовать, пусть даже маленькая, погрешность измерения. Самое печальное, что погрешности чаще всего являются случайными, то есть при каждом измерении оказываются разными и неизвестными экипажу. В результате пилот никогда не знает точных значений измеряемых параметров и в принципе не может абсолютно точно выполнить полет по заданной траектории.

Проблемы оценки точности навигации подробно рассматриваются в дисциплине «Аэронавигационное обеспечение полетов». Но иметь определенное представление о точности навигационных средств необходимо уже и при изучении самой аэронавигации, поскольку без этого невозможно грамотно применять различные радионавигационные системы. Этому и посвящен данный параграф учебного пособия, в котором рассмотрены минимально необходимые понятия.

Погрешность и поправка. Любое измерение сопровождается погрешностями.

Погрешность – разность между измеренным и фактическим значениями измеряемой величины. Ранее для этого же понятия использовался термин «ошибка» и рассматривались, например, «ошибки измерения» навигационных параметров. Сейчас термин «ошибка» используется только применительно к неправильным действиям человека.

Пусть с помощью некоторого прибора измеряется некая абстрактная величина (обозначим ее a), которая на самом деле (фактически) имеет значение a_фак , которое мы и пытаемся узнать в результате измерения. Вследствие несовершенства прибора и множества других факторов прибор показывает измеренное значение a_изм , которое отличается от фактического. Тогда погрешность Δa составит

Δa= a_изм - a_фак.

Следует обратить внимание, что для получения погрешности с правильным знаком необходимо из измеренного значения вычесть фактическое, а не наоборот.

Из трех величин, входящих в данную простую формулу, пилоту известна только одна – то, что показывает прибор, то есть a_изм .Ему не известно фактическое значение величины (в противном случае – зачем тогда ее измерять?) и, следовательно, неизвестна погрешность измерения.

Но если бы погрешность измерения была бы известна, можно было бы по измеренному значению найти и фактическое значение. Достаточно было бы вычесть из результата измерения величину погрешности.

Вычесть число – это то же самое, что прибавить число, противоположное по знаку. Величина, которую нужно прибавить к результату измерения, чтобы получить фактическое значение величины называется поправкой. Очевидно, что погрешность и поправка различаются только знаком, а по модулю одинаковы.

В литературе погрешности и поправки очень часто обозначают одинаково, одними и теми же буквами. Например, Δa может обозначать как погрешность, так и поправку. Разумеется это может вызвать путаницу.

Пусть Δa – погрешность, а δa – поправка, то есть δa= - Δa. Тогда

a_фак = a_изм –Δa=a_изм + δa.

То есть, для получения фактического значения нужно к измеренному значению прибавить поправку (это то же самое, что вычесть погрешность).

Отсюда как раз и вытекает очень полезное для навигации правило учета поправок: при переходе от приборных (измеренных) величин к более истинным (фактическим) поправки прибавляются, а при переходе от истинных к приборным – вычитаются. Разумеется, при прибавлении и вычитании учитывается и собственный знак поправки, ведь она может оказаться как с плюсом, так и с минусом.

Виды погрешностей. Практически всегда погрешность включает в себя две составляющие ее части: систематическую и случайную.

Δa= Δa_сист + Δa_случ .

Систематической называется погрешность, которая в данных условиях сохраняет постоянное значение (или изменяется, но по известному закону).

Такие погрешности вызваны постоянно действующими причинами, в результате чего при измерении мы каждый раз «ошибаемся» на одну и ту же величину. Очень часто такие погрешности вызваны неточным изготовлением прибора (инструментальные погрешности), или постоянным внешним фактором. Например, собственное магнитное поле самолета вызывает погрешность измерения магнитного курса (девиацию), которая на каждом курсе имеет вполне определенное значение.

Систематические погрешности, поскольку они одинаковы при каждом измерении, можно один раз определить с помощью более точных приборов, а затем исключать их из результатов измерений путем ввода поправок. Например, бортовые таблицы к высотомерам, указателям скорости, компасам как раз и предназначены для ввода в результаты измерений поправок, устраняющих систематические погрешности. Таким образом, систематические погрешности не доставляют особых хлопот при навигации, поскольку после их устранения они уже отсутствуют. Поэтому далее будем считать, что систематические погрешности отсутствуют (уже учтены).

Случайная погрешность при каждом измерении принимает разное значение, причем заранее неизвестно какое именно.

А вот случайные погрешности в принципе устранить нельзя, поскольку они при каждом измерении различны. И они всегда остаются неизвестными. Ведь чтобы по результату измерения узнать погрешность необходимо сравнить этот результат с точным значением измеряемой величины. Но оно нам неизвестно – иначе, зачем мы вообще проводили измерения? Таким образом, пилоту приходится осуществлять навигацию, основываясь на неточных результатах измерения, которые содержат неизвестные ему случайные погрешности.

Определить численные значения случайных погрешностей невозможно, однако пилот постоянно должен иметь в виду, что эти погрешности существуют и иметь представление об их возможных значениях. Наличие неопределенности в результатах измерений является одним из основных факторов, усложняющих навигацию и делающих ее не только наукой, и искусством.

Вообще случайные величины рассматриваются в разделе математики, называемом теорией вероятностей. Рассмотрим некоторые основные понятия этой теории, которые будут необходимы в дальнейшем.

Случайным событием называют событие, которое при данных условиях может произойти или не произойти. Степень возможности наступления такого события численно характеризуют величиной вероятности. Вероятность Р– это число, которое может лежать в пределах от 0 до 1. Если при данных условиях событие никогда не происходит, его называют невозможным событием и его вероятность равна нулю. Если же оно при данных условиях происходит всегда, то его называют достоверным и приписывают ему вероятность равную единице. Если, например, Р=0,3 , то это означает, что в среднем в 30 случаях из 100 событие произойдет. Именно в среднем, поскольку событие является случайным. Если создать необходимые для наступления события условия и провести серию из 100 опытов, то событие может произойти, например, 23 раза, или 32 раза… Если провести несколько серий таких опытов, или одну серию из тысячи, десяти тысяч, миллиона опытов, то, чем большее количество опытов проведено, тем ближе среднее количество наступлений события будет ближе к 30% от общего количества опытов (если Р=0,3).

Каким же образом можно описать случайные погрешности, если они не имеют какого-либо определенного значения? Часто их характеризуют величиной средней квадратической погрешности (СКП), которая обозначается буквой σ (сигма). Так, например, СКП измерения величины a будем обозначать σa.

СКП является характеристикой степени рассеяния измеренного значения величины вокруг фактического ее значения. Чем больше σa . тем больше рассеяны (разбросаны) измеренные в разных опытах значения вокруг фактического значения величины.

На рис. 2.19 геометрически представлены в виде числовой оси возможные значения измеряемой величины a и отмечено фактическое ее значение. Крестиками на шкале обозначены полученные в результате нескольких опытов измеренные значения. В первом случае разброс измеренных значений вокруг фактического больше, чем во втором случае, следовательно «сигма», которая и характеризует степень разброса, во втором случае меньше.

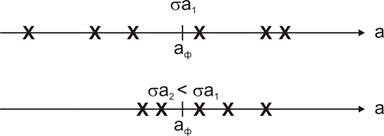
Рис. 2.19. Средняя квадратическая погрешность

По величине СКП можно судить о вероятностях того, что измеренное значение примет то или иное значение. Но для этого недостаточно знать СКП, нужно также знать, какому закону распределения подчиняется данная случайная погрешность. Многие случайные величины подчиняются нормальному (гауссовскому) закону распределения. Для этого закона полезно запомнить следующие значения.

Если систематическая погрешность отсутствует и в результате измерения получено значение a_изм, то фактическое значение величины лежит в пределах (рис. 2.20):

a_изм ± σa с вероятностью Р=0,68;

a_изм ± 2σa с вероятностью Р=0,95;

a_изм ± 3σa с вероятностью Р=0,997.

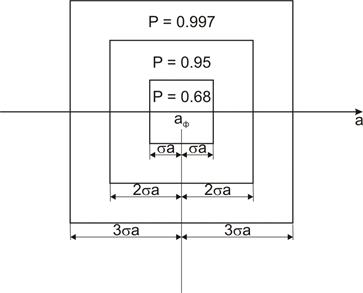
Рис. 2.20. Некоторые вероятности для нормального закона распределения

Например, с помощью компаса измерен курс γ=100º , а точность компаса характеризуется СКП σγ =2º . Это означает, что фактический курс (который так и останется нам неизвестным) в среднем:

в 68 случаях из 100 лежит в пределах 100º ±2º, то есть в интервале 98º …102 º;

в 95 случаях из 100 лежит в пределах 100º ±4º, то есть в интервале 96º …104º;

в 997 случаях из 1000 лежит в пределах 100º ±6º, то есть в интервале 94º …106º.

Значение вероятности Р=0,997 настолько близко к единице, что соответствующее ей значение погрешности в «три сигмы» часто называют максимальной погрешностью. На самом деле погрешность может его и превысить. Правда, редко – в среднем в трех случаях из тысячи.

В технических описаниях приборов и оборудования их точность может быть указана непосредственно в виде СКП и тогда все понятно. Но иногда ее указывают, например, так: «погрешность измерения пеленга ±1,5º». Разумеется, это не означает, что такой пеленгатор «ошибается» каждый раз на 1,5º . Это также не означает, что он не может ошибиться более, чем на 1,5º. Как правило, указанное таким образом значение погрешности соответствует вероятности Р=0,95. То есть в среднем в 95 случаях из 100 погрешность не превысит (в большую или меньшую сторону) значения в 1,5º. Соответственно, в пяти случаях из ста погрешность может быть и больше. Для нормального закона распределения погрешности вероятность 0,95 соответствует удвоенной СКП. Следовательно, СКП измерения пеленга в данном примере составит 0,75º.