Формы и размеры Земли

Для воздушной навигации необходима система координат для определения местоположения ВС и положение точек на земной поверхности .Значение

координат может быть выражено угловыми и линейными величинами Свойства системы координат зависят от формы поверхности, на которой она задана. Поэтому необходимо выяснить, какую форму имеет Земля как планета.

Поверхность, ограничивающая Землю как физическое тело, называется физической поверхностью Земли. Поверхность Земли носит сложный нерегулярный характер, обусловленный неровностями рельефа: горами, равнинами, впадинами. На такой поверхности ввести какую-либо приемлемую для практики систему координат невозможно, поэтому необходимо эту поверхность каким-то образом «сгладить». Для этого используется понятие уровенной поверхности В качестве сглаженной фигуры Земли разумно выбрать форму уровенной поверхности, совпадающей с физической поверхностью в морях и океанах, где нет неровностей рельефа. Такая фигура получила название геоида.

Геоид(geoid) - это фигура, образованная уровенной поверхностью, совпадающей в морях, и океанах с их средней поверхностью. В районах материков поверхность геоида проходит под уровнем рельефа местности. Эту поверхность и называют средним уровнем моря, от которого отсчитывают высоту рельефа и другие высоты. В России за начало уровня отсчета высот принято нулевое деление футштока (мерной линейки), установленной в Обводном канале г.Кронштадт.

Поверхность геоида хотя и является гладкой по сравнению с физической поверхностью Земли, но все же имеет неправильную форму.Геоид не имеет простого математического описания.Поэтому для упрощения вычислений расстояний и направлений его замняют эллипсоидом вращения.который имеет правильную геомЕтрическую форму и незначительно отличается от геоида .

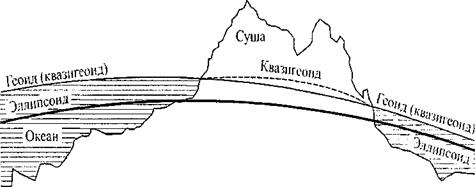Рис.1. Для удобства навигационных расчетов форму Земли представляют виде шара с незначитльным сжатием у полюсов.Этот элипс имеет следующие размеры:экваториальный радиус а=6378 км, полярный радиус в=6357км.

В воздушной навигации в большинстве случаях сжатием Земли пренебрегают и принимают Землю условно за шар с R=6371КМ.при таком допуске максимальная ошибка в определении длин не превышает 0,5%,а в определение направлений 12 минут,чем в практике обычно пренебрегают.

Наиболее точное измерение Земли произведены в 1941г советским ученым Кросовским.

Рис. 1.2. Эллипс и его параметры

Каждое государство старается выбрать такие параметры эллипсоида и так его разместить в теле Земли, чтобы его поверхность как можно ближе подходила к поверхности геоида на территории данного государства (при этом в других частях Земли отклонения могут быть большими). Поэтому существует много референц-эллипсоидов, принятых в разных странах и в разные годы..

Если очень высокая точность решения навигационных задач не требуется, то Землю можно рассматривать как сферу. В этом случае используется нормальная сферическая система координат, полюсы которой совпадают с географическими полюсами нашей планеты, т.е. точками, в которых оси вращения Земли пересекает ее поверхность. Система координат на сфере строится с помощью больших кругов.

ИКАО приняло решение с 1 января 1998 г. публиковать в документах аэронавигационной информации координаты пунктов в единой для всего мира системе координат, называемой WGS-84 (World Geodetic System).

Большим кругом (Great Circle, G/C)) называется окружность, образующаяся в результате сечения сферы плоскостью, проходящей через центр Землин