Понятие о звене и его статических характеристиках
Изображение элементов с указанием связи между ними называется структурной схемой. Элемент структурной схемы с выделенным входом и выходом называется звеном. Звенья системы имеют статические и динамические характеристики.
Статической характеристикой называется зависимость выходного сигнала звена от входного в установившемся режиме у=f(x)êt®¥.
Если статическая характеристика описывается уравнением прямой линии у=kx+b, то и звено и характеристика называются линейными.
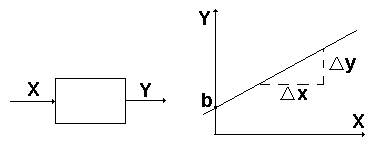
b – константа, зависит от выбора начала отсчета;
k – коэффициент передачи звена 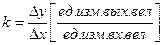
Если хотя бы одно звено системы является нелинейным, то и вся система считается нелинейной. Реально все элементы являются в той или иной степени нелинейными, но некоторыми нелинейностями можно пренебречь. Другие обладают гладкими характеристиками и, вводя предположение о малых отклонениях переменных относительно установившегося значения, можно линеаризовать характеристики элементов.
Для непрерывной функции у=f(x), имеющей n непрерывных производных в окрестностях точки линеаризации (у0, х0), степенной ряд Тейлора имеет вид:
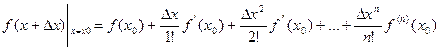
Если отбросить нелинейные члены разложения получим линейное приближение:
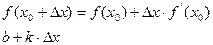
Отсюда следует графический смысл этого метода линеаризации:
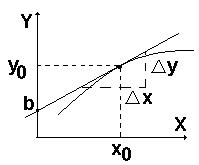
Мы заменяем кривую отрезком касательной к этой кривой в рабочей точке: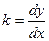
Результаты линеаризации b и k справедливы только в окрестностях точки линеаризации.
Существуют звенья, у которых не наступает установившийся режим выходной величины. Например: входная величина – приток, выходная – уровень. Двигатель: входная величина – напряжение, выходная – угол поворота.
Если нет установившегося значения выходной величины, то нельзя и построить статическую характеристику. Такие звенья называют астатические.
Дата добавления: 2015-06-22; просмотров: 1172;
