Классификация низкоразмерных систем

Полупроводниковые материалы называются низкоразмерными, когда один геометрический параметр имеет длину порядка длины волны де Бройля .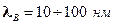

Спектральные характеристики представлены на рис.

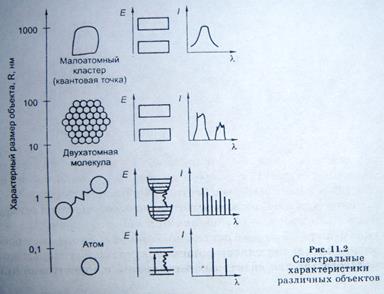
Рис. Для атома, двухатомной молекулы, квантовой точки и объемного материала представлены-- характерные размеры, энергетические диаграммы и спектры.

Энергия Ферми для электронных систем с низкой размерностью приведена в табл

табл

	Электронная система			Энергия Ферми
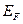
Квантовая проволока	одномерная		1D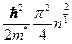
Квантовая яма	двумерная		2D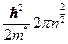
Квантовая точка	трехмерная		0D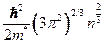

Квантовые эффекты проявляются, начиная с квантовых ям, когда движение электронов ограничено нанометровыми размерами в одном измерении.

Плотность энергетических состояний для размерных объектов показана на рис

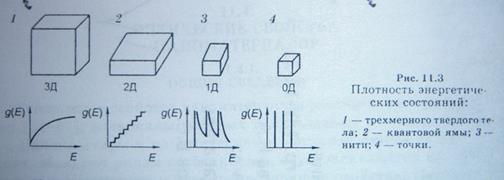
Рис. Плотность энергетических состояний объемного твердого тела, квантовой ямы, нити, и точки.

Квантовые ямы, проволоки и точки,

Квантовые яма – образец, один размер которого лежит в нанодиапазоне, а два других в микродиапазоне и выше. Пример (графен, монослой, нанослой на подложке, нанопленка).

Примером квантовой ямы является двумерная полупроводниковая структура состоящая из трех слоев. Пленка арсенида галлия 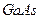нанометровой толщины с зоной (1,4 эв), окружена с обеих сторон слоями алюмината арсенида галлия с 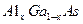с более широкой запрещенной зоной(2 эв) при 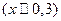.В результате возникает профиль потенциальной энергии. близкий к по форме к прямоугольному с высотой барьера 0,4 эв для электронов и для дырок 0,2 эВ.

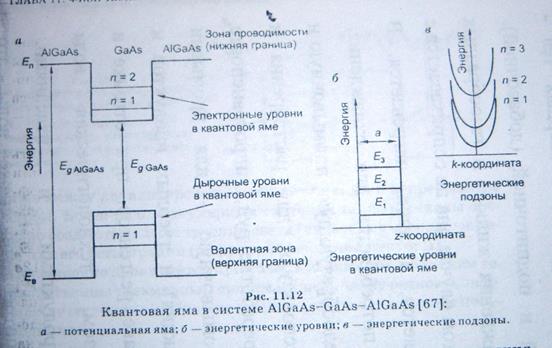
Рис.а)Прямоугольная потенциальная яма в трехслойной системе .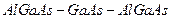

б)энергетические уровни.,в) энергетические подзоны.

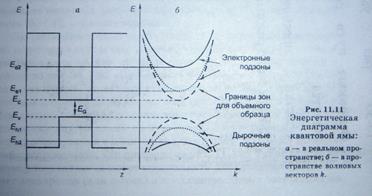
Рис. Энергетическая диаграмма квантовой ямы.. а) в энергетическом пространстве,

б) в пространстве волновых векторов.

В направлении оси z движение электронов ограничено и квантуется, в плоскости 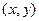остается свободным. Поэтому волновая функция электронов в квантовой яме принимает вид

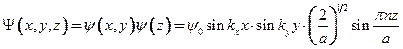
Энергия электронов квантуется по оси :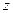

. .

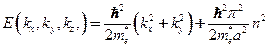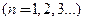Где 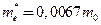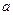- ширина квантовой ямы

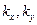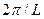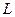Квазинепрерывные значения волновых векторов определяются периодическими граничными условиями. , где -размер образца в плоскости.

Плотность состояний для двумерной электронной системы

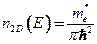
в интервале 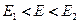электроны располагаются в подзоне с 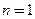. В интервале 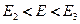электроны располагаются в двух подзонах 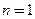и 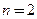и плотность состояний удваивается. График полной плотности состояний в зависимости от роста энергии имеет ступенчатый характер с постоянной величиной ступеньки 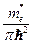по оси ординат и энергии 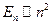по оси абцисс. Ступенчатый характер функции 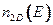подтверждается прямыми измерениями оптического поглощения.см рис мартин 133.+

Рис.Функция плотности состояний для двумерной электронной системы.

Квантовая проволока –образец, два размера которого лежат в нанодиапазоне и один в микродиапазоне и выше. пример (нанопроволока, молекула ДНК)

В квантовых проволоках электронный газ свободно движется по оси 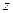. По двум другим направлениям движение электронов ограничено и квантуется. Двумерное уравнение Шредингера имеет вид:

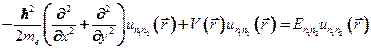, где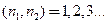

Полная энергия электрона в квантовой проволоке для двумерного прямоугольного потенциала бесконечной длины 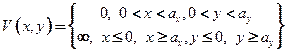следующая

.

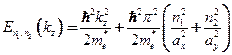В случае квантовых проволок энергетические уровни соответствующие поперечному движению описываются двумя квантовыми числами. Значения уровней энергии для электронных состояний возрастают при уменьшении толщины квантовых проволок.

Плотность состояний одномерного электронного газа

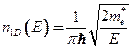
Представляется в виде узкого пика: слева это прямая 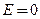, справа асимптота .

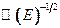см рис. Учитывая, что 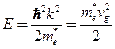получаем

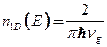где 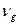-групповая скорость

Электрический ток в одномерной системе .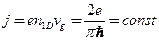

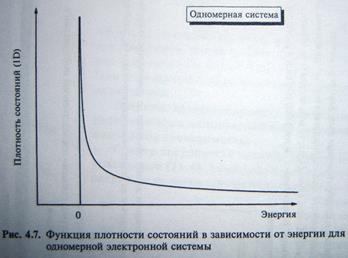
Рис. Функция плотности состояний в зависимости от энергии для одномерной электронной системы. (квантовая проволока.)

Квантовая точка – это образец (нанокристаллл), все три размера которого лежат в нанодиапазоне. Пример (нанокластер). Примеры показаны на рис Пул199. Структуры получают нанолитографией. Реальные вантовые точки содержат большое число атомов до10⁴-10⁶. Энергетический спектр соответствует трехмерному потенциальному ящику.

Уравнение Шредингера имеет вид

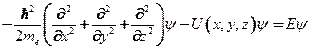
Волновыми фикциями являются стоячие волны

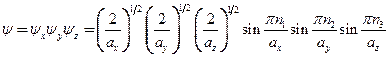
и энергетические уровни

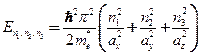
Функция плотности состояний квантовой точки представляет собой набор пиков дельта функций 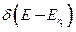.Квантовой точке отвечает неэвидистантный дискретный спектр 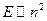, атомной системе энергия 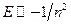. Плотность энергетических состояний для квантовых ям ,проволок и точек смна рис..

Квантовые точки создаются методом молекулярно-лучевой эпитаксии. Спонтанное формирование массивов вертикально связанных квантовых точек-нанкластеров осуществляется в режиме Странского –Крастанова. См в лекции мол.луч. эпитакс.

Метод самоорганизации квантовых точек на поверхности раздела двух материалов с разными параметрами кристаллической решетки. Материал 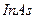выращивается химическим осаждением паров из газовой фазы на подложке из кристалла с большой постоянной кристаллической решетки и большой шириной запрещенной зоны 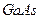. Возникающие пирамидки рассматриваются как примесные дефекты на поверхности основного полупроводника. Эти дефекты приводят к появлению электронных уровней ниже зоны проводимости и дырочных уровней энергии выше валентной зоны .см рис

Рис. экспериментальная полупроводниковая реализация квантовой точки в виде пирамидки 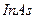на поверхности .

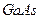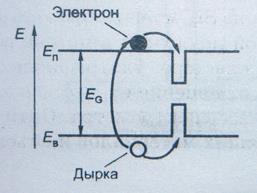
Рис. Зонная структура полупроводника содержащего квантовую точку.

Оптические свойства квантовых точек (0D -системы)

Общими свойствами нульмерных ограниченных систем являются: уширение запрещенной зоны, повышение силы осцилляторов, особенности поглощения падающего света, уширение спектра.

Уширение запрещенной зоны - важнейшая особенность квантовых точек по сравнению с массивным образцом. В режиме «сильной локализации» когда размер квантовой точки меньше радиуса экситона, энергия квантовой локализации превышает энергию кулоновского взаимодействия.

Повышение силы осцилляторов. По мере уменьшения размерности системы от 3D к 0D плотность энергии электронных состояний возрастает, и возрастают силы осцилляторов соответствующие оптическим переходам. Концентрация энергетических состояний используется для повышения коэффициента усиления лазерных устройств. При уменьшении размерности системы сильнее проявляются электрооптические эффекты, которые используются для создания оптоэлектронных модуляторов на квантовых ямах.

Особенности поглощения падающего света. Межподзонные оптические переходы в двумерных системах разрешены, если свет распространяется в плоскости квантовой ямы, т.е. когда электрическое поле фотона перпендикулярно поверхности раздела. Квантовые точки способны поглощать свет с любого направления. Локализация по трем оптическим осям означает, что волновые функции электронов тоже квантуются по трем пространственным направлениям.

Уширение спектра. Оптические спектры квантовых точек не зависят от температуры. Ширина спектральных линий не зависит от температуры, так как эти линии дискретные. При высокой однородности размеров квантовых точек ширина линий составляет 0,01 эв.