Проведение возбуждение по нервным волокнам

В основе развития процесса проведения возбуждения по нервным волокнам наряду с ПД участвуют пассивные электрические свойства мембраны нервных волокон, которые определяются на эквивалентной схеме нервного волокна, погруженного в проводящую среду (Рис):

Сопротивление мембраны (r_m) рассчитывается через удельное сопротивление (R_m):

,

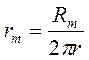где: R_m=1-100 кОм·см², в перехватах Ранвье: 30-40 Ом·см²

Сопротивление аксоплазмы (r_i) рассчитывается через удельное сопротивление (r_i):

,

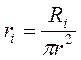где: R_i=40 Ом·см.

Емкость мембраны (c_m) рассчитывается через удельную емкость мембраны (С_m):

,

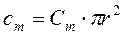где: С_m=1мкФ/см^2, в перехватах Ранвье:3-4 мкф/см², r –радиус нервного волокна, R,C –удельные и r,c- относительные значения сопротивления и емкости мембраны (m) и аксоплазмы (i) в рассчете на единицу длины или площади мембраны.

Возвращаясь к выше представленному выражению для расчета мембранного тока:

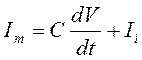
следует определить согласно эквивалентной электрической схеме, что мембранный ток аксиального направления будет равен согласно закону Кирхгофа:

,

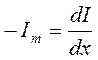В свою очередь согласно закону Ома ток, текущий через аксоплазму равен:

, а итоговый: .

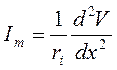В окончательном виде:

;

; .

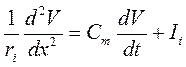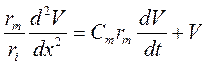С учетом того, что

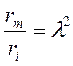и ,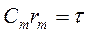

окончательное выражение принимает вид:

.

Решение этого уравнения требует ряд упрощений:

1. При аксиальном введении регистрирующего электрода мембранный ток становится равным нулю и тогда:

,

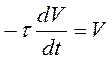решением этого уравнения является экспоненциальная зависимость:

,

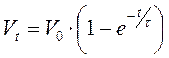где τ – постоянная времени, показывающая через сколько времени амплитуда мембранного потенциала падает в e раз.

2. При коротком стимуле емкостная составляющая будет равна нулю и тогда:

,

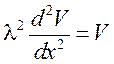где решение: 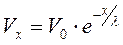и l – постоянная длины, показывающая через какое расстояние амплитуда мембранного потенциала падает в e раз. С учетом сопротивлений мембраны и аксоплазмы (R_m и R_i):

,

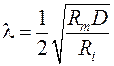где: D – диаметр нервного волокна (D = 2r).

Таким образом, определяющая скорость проведения возбуждения постоянная длины (λ) прямо пропорциональна параметрам нервного волокна.

В итоге, скорость проведения возбуждения:

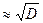для безмиелинового и 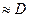для миелиновых волокон.

Из уравнения:

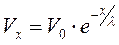
,где:

I₀ – начальный ионный ток, R_X – входное сопротивление, важное значение для дальнейшей судьбы распространяющегося ПД имеет последняя компонента.

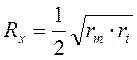
и с учетом удельных значений:

,

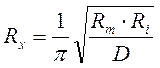где: D – диаметр нервного волокна.

Таким образом, входное сопротивление нервного волокна, от которого зависит скорость распространения нервного импульса, также связана с диаметром этого волокна. Это означает, что с уменьшением диаметра нервного волокна входное сопротивление мембраны значительно возрастает, а при уменьшении – падает. Это явление определяет зависимость скорости проведения возбуждения от геометрических и функциональных неоднородностей нервных волокон. Резкое падение входного сопротивления мембраны будет подобно феномену “перегрузка генератора” в электрической цепи и замедлять проведение возбуждения вплоть до выпадения отдельных нервных импульсов и наоборот – “облегчать” проведение возбуждения при росте входного сопротивления в случае уменьшения диаметра нервного волокна.

Распространение потенциала действия вдоль мембраны нервного волокна будет неодинаково, и из-за этого возникают локальные токи, посредством чего и происходит распространение возбуждения. В каждой точке генерируется новый ПД, однако, проводится не он, а возбуждение в виде локальных токов-пусковых механизмов для новых ПД.

Представим, что в точке V_J мембранный ток (I_m) складывается из притекающего и оттекающего токов:

,

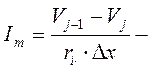
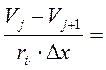
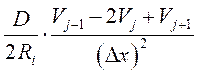где: D – диаметр аксона, R_i- сопротивление аксоплазмы.

Как видно из выражения роль локального тока играет мембранный ток и его характеристики относительно ионных проницаемостей и ПД можно увидеть на Рис.

1. В начале доминирует ток из V_J-1 в V_J, так как первый участок заряжен относительно второго положительно. Этот процесс приводит к деполяризации в точке V_J.

2. В следующей фазе преобладает ток V_J в V_J+1, по выше описанной схеме, так как уже этот участок (V_J) становится положительно заряженным относительно второго.

3. Наконец от возбужденного участка V_J+1 ток течет назад к V_J, вызывая дополнительную деполяризацию мембраны.

На пике первой фазы открываются натриевые каналы, и они забивают мембранный ток, в результате чего он не может внести заметных изменений в I_m, и его падение в отрицательную фазу I_Na замедлено. В результате условием развития ПД будет равенство входящего (I_Na) и выходящего суммарных токов:

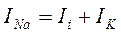
К моменту развития ПД суммарный ионный ток приобретает входящее направление и из уравнения:

,

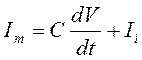где в момент развития ПД емкостная составляющая равна нулю и:

.

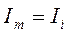Эта величина ионного тока получила название ξ-потенциал.

К моменту развития ПД суммарный ионный ток приобретает входящее направление, совпадающее по максимуму с точкой максимальной скорости нарастания ПД. Этот процесс обеспечивает развитие ПД, хотя в точке максимума ПД ионный ток равен нулю. В фазу реполяризации мембраны вновь появляется ионный ток противоположного направления, соответствующий максимальной амплитуде точке максимального снижения ПД.