Модуль упругости

При течении тело испытывает сдвиговую деформацию, кроме того, вязкотекучее и высокоэластическое состояния полимера принципиально ничем не отличаются, поэтому для этих условий справедливо соотношение:

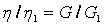
Соответственно и уравнение Муни применимо для описания G наполненных эластомеров. Однако для полимеров, находящихся в стеклообразном или кристаллическом состояниях, уравнение Муни дает резко завышенные результаты. Это обусловлено отклонением коэффициента Пуассона (ν) матрицы от значения 0,5, характерного для газа, жидкостей и эластомеров. Для жестких полимеров с твердыми частицами модуль упругости можно рассчитать по уравнению Кернера:

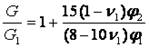
В этом уравнении не учитываются практически никакие геометрические характеристики наполнителя (размер, форма). Поэтому оно справедливо только для сферических частиц при невысоких степенях наполнения.

Более общее уравнение представили Льюис и Нильсен:

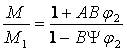
где А, В, Ψ – константы. Константа А учитывает форму и размер частиц наполнителя:

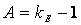
Константа В учитывает соотношение модулей упругости фаз:

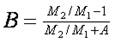
При большой разнице в модулях упругости полимера и наполнителя, что обычно имеет место, В близок к единице. Константа Ψ учитывает φ_m:

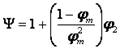
Необходимо отметить, что и это уравнение не работает при приближении концентрации наполнителя к φ_m.