Реологические свойства

Реология – наука о течении. Течение – это направленное перемещение молекул вещества относительно друг друга под действием внешних сил. Основная характеристика реологического поведения жидкости – это вязкость, которая характеризует сопротивляемость жидкости течению и определяется энергией межмолекулярного взаимодействия. В данном случае мы будем рассматривать ПКМ как суспензию дисперсных частиц в вязкотекучей жидкости.

Поскольку твердая частица не деформируется вместе со слоями окружающей жидкости, то она будет препятствовать течению жидкости и повышать ее вязкость. Повышают сопротивление течению и адсорбированные на наполнителе макромолекулы и образующаяся коагуляционная сетка наполнителя. Кроме того, возможны столкновения частиц при течении и затраты энергии на их взаимное трение, что также повышает вязкость системы. Понятно, что с увеличением концентрации наполнителя влияние этих факторов увеличивается и вязкость растет. Но этот рост не пропорционален содержанию наполнителя.

Первым уравнением, теоретически описывающим поведение суспензий, было уравнение Эйнштейна:

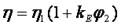
где η, η₁ – вязкости суспензии и жидкой фазы; k_Е – коэффициент Эйнштейна, φ₂ – объемная доля твердых частиц.

Из уравнения Эйнштейна следует, что зависимость вязкости суспензии от количества наполнителя имеет линейный характер, а крутизна увеличения вязкости определяется коэффициентом k_E. Однако, как уже отмечалось, рассматриваемая зависимость нелинейная, с увеличением концентрации наполнителя степень его влияния на вязкость возрастает, и при приближении φ₂ к φ_m вязкость суспензии резко возрастает. Уравнение Эйнштейна удовлетворительно описывает только дисперсии с очень низкой концентрацией твердых частиц.

Имеется более ста уравнений, описывающих вязкость суспензий. Из этих уравнений наиболее широкое применение нашло уравнение Муни:

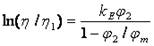
При приближении φ₂ к φ_m отношение вязкости композиции к вязкости полимера стремится к бесконечности. Это уравнение довольно хорошо описывает вязкость различных суспензий в широком интервале концентраций.

Имеется еще одно уравнение, которое без учета k_Е хорошо описывает экспериментальные зависимости вязкости различных суспензий от содержания твердых частиц:

.

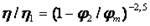Параметры k_Е и φ_m характеризуют форму частиц наполнителя. Уравнение показывает, что влияние формы частиц на вязкость можно учесть, используя всего один из этих параметров – φ_m.