Поток солнечной радиации, приходящийся на 1 м2 площади границы земной атмосферы, составляет 1350 Вт. Эту величину называют солнечной постоянной. 3 страница
Электроны с одинаковым главным квантовым числом образуют слой. Слои обозначают буквами К, L, М, N и т. д. в соответствии с п = 1, 2, 3, 4, ... . Электроны, имеющие одинаковые пары значений n и l, входят в состав оболочки, которая кратко обозначается так же, как соответствующие состояния для электрона атома водорода: 1s, 2s, 2р и т. д. Так, например, называют 2в-оболочка, 2в-электроны и т. п.
Число электронов в оболочке обозначают справа вверху около символической записи оболочки, например 2p4.
Распределение электронов по оболочкам в атоме (электронные конфигурации) обычно указывают следующим образом: для азота (Z = 7) — Is2, 2s2, 2р3; для кальция (Z = 20) — Is2, 2s2, 2р6, 3s2, Зр6, 4s2 и т. д.
Так как энергия электронов сложных атомов зависит не только от n, но и от l, то построение таблицы Менделеева не всегда происходит постепенным заполнением слоев по мере усложнения атома. У калия (Z = 19), например, вместо заполнения слоя М (что соответствовало бы конфигурации Is2, 2s2, 2p6, 3s2, Зр6, 3d1) начинается заполнение слоя N и создается следующая электронная конфигурация: Is2, 2s2, 2р6, 3s2, Зр6, 4s1. Аналогичные отклонения от «регулярного» заполнения слоев имеются и у некоторых других элементов.
Всегда выполняется общее правило: электроны невозбужденного атома занимают состояние с наименьшей энергией и в соответствии с принципом Паули. На рис. 23.11 схематически без соблюдения масштаба показаны энергетические состояния и уровни сложного атома и соответствующее им число электронов.
 В заключение отметим, что состояние многоэлектронного атома в целом определяется следующими квантовыми числами: L — квантовым числом полного орбитального момента атома1, которое принимает значения 0, 1, 2, 3 и т. д.; J — квантовым числом полного момента атома, которое может принимать значения с интервалом в единицу от \L - S\ до L + S; S — квантовым числом результирующего спинового момента атома; магнитным квантовым числом то,, которое определяет дискретные значения проекции полного момента импульса атома LA на некоторую ось Z:
В заключение отметим, что состояние многоэлектронного атома в целом определяется следующими квантовыми числами: L — квантовым числом полного орбитального момента атома1, которое принимает значения 0, 1, 2, 3 и т. д.; J — квантовым числом полного момента атома, которое может принимать значения с интервалом в единицу от \L - S\ до L + S; S — квантовым числом результирующего спинового момента атома; магнитным квантовым числом то,, которое определяет дискретные значения проекции полного момента импульса атома LA на некоторую ось Z:
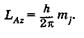 (23.37)
(23.37)
При заданном J квантовое число т.- принимает 2J+ 1 значений: -J, -J +1, ..., +J.
§ 23.9. Энергетические уровни молекул
Энергетические уровни молекул имеют более сложное строение, чем у атомов. Это вызвано тем, что в молекуле, кроме движения электронов относительно ядер, происходит колебательное движение атомов около их положения равновесия (колебание ядер вместе с окружающими их электронами) и вращательное движение молекулы как целого.
Электронному, колебательному и вращательному движениям молекулы соответствуют три типа уровней энергии: Еэл, Екол и Евр.
Согласно квантовой механике, энергия всех видов движения в молекуле принимает только дискретные значения (квантуется). Полная энергия Е молекулы может быть представлена суммой квантованных значений энергии разных видов:
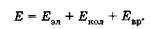 (23.38)
(23.38)
На рис. 23.12 схематически изображена система уровней молекулы! далеко отстоящие электронные уровни энергии а' и а", для которых Екол = Евр = 0; более близко расположенные колебательные уровни v' и v", для которых Евр = 0; наиболее тесно расположенные вращательные уровни J' и J" с различными значениями Е .
«Расстояние» между электронными уровнями энергии примерно 1—10 эВ, между соседними колебательными уровнями — 10 -2— 10 -1 эВ, между соседними вращательными уровнями — 10 -5—10 -3 эВ.
 Квантование колебательной энергии двухатомной молекулы можно объяснить, если рассматривать молекулу как гармонический осциллятор. Допустим, что атомы сопротивляются смещению из положения равновесия с силой
Квантование колебательной энергии двухатомной молекулы можно объяснить, если рассматривать молекулу как гармонический осциллятор. Допустим, что атомы сопротивляются смещению из положения равновесия с силой 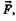 пропорциональной вели-
пропорциональной вели-
чине смещения х, тогда, следуя закону Гука (см. § 5.1), можно написать выражение для частоты колебаний двухатомного осциллятора (вибратора)
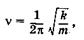 (23.39)
(23.39)
где k — является мерой «упругости», или силы химической связи между атомами. Чем выше упругость или меньше масса атомов, тем выше частота колебаний.
На основании (5.25) можно написать выражение для потенциальной энергии осциллятора
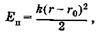 (23.40)
(23.40)
где (г - г0) — смещение относительно положения равновесия. Подставив (23.40) в уравнение Шредингера (23.14), получим
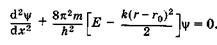 (23.41)
(23.41)
Решение уравнения (23.41) дает выражение для полной энергии колебаний Екол
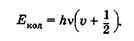 (23.42)
(23.42)
Величина v — колебательное квантовое число, которое может принимать значения 0, 1, 2, ...и т. д.
При аппроксимации двухатомной молекулы моделью гармонического осциллятора график зависимости потенциальной энергии (23.40) от межатомного расстояния (рис. 23.13) представляет собой параболу с равноотстоящими уровнями колебательной энергии. Горизонтальные кривые соответствуют Екол — полной энергии (кинетическая плюс потенциальная) вибратора на колебательных уровнях, характеризуемых значениями v = 0, 1, 2 и т. д.
Интересно, что даже на нижнем колебательном уровне (и = 0) в точке г = г0, соответствующей положению равновесия, молекула обладает половиной кванта колебательной энергии (см. рис. 23.14). Для молекулярного водорода это составляет 0,269 эВ. Молекула сохраняет такую колебательную энергию даже при абсолютном нуле.
Рассмотрим молекулу с колебательным уровнем v = 2 и первоначально находящуюся в состоянии сжатия (в точке С, межъядерное расстояние rc). Тогда вся энергия будет потенциальной, и кинетическая энергия осциллятора равна нулю. Такая молекула может колебаться между точками С и С. В точке r= г0 кинетическая энергия будет достигать максимума, а потенциальная будет равняться нулю.
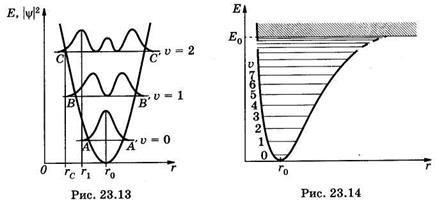
Используя приближение классического осциллятора, можно предсказать, что максимальное смещение при колебательном движении соответствует двум точкам поворота С и С и что осциллятор должен находиться большую часть времени вблизи этих точек. Квантовая механика также предсказывает значения наибольшей плотности вероятности нахождения атомов в областях вблизи точек поворота, но значительно смещенных к центру (межъядерное расстояние г1). Это показано на рис. 23.13, где распределение плотности
вероятности 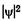 представлено для колебательных уровней двухатомной молекулы в зависимости от расстояния г между томами молекулярного гармонического осциллятора. Вместо простой классической картины с двумя максимумами вероятности (в точках А и А', В и В', С и С’) рис. 23.13 дает
представлено для колебательных уровней двухатомной молекулы в зависимости от расстояния г между томами молекулярного гармонического осциллятора. Вместо простой классической картины с двумя максимумами вероятности (в точках А и А', В и В', С и С’) рис. 23.13 дает 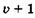 максимумов. При этом на нижнем колебательном уровне наиболее вероятно нахождение молекулы в положении r0, а на более высоких уровнях — ближе к областям точек поворота.
максимумов. При этом на нижнем колебательном уровне наиболее вероятно нахождение молекулы в положении r0, а на более высоких уровнях — ближе к областям точек поворота.
Модель гармонического осциллятора удовлетворительно описывает колебание двухатомной молекулы лишь при небольших смещениях r - r0, тогда как разрыв химических связей происходит при значительных смещениях ядер. Реальные кривые потенциальной энергии асимметричны, как это показано на рис. 23.14 на примере молекулы водорода. Гармонический осциллятор предсказывает серию равноотстоящих уровней колебательной энергии, однако в действительности (при асимметрии потенциальной кривой) уровни сгущаются с ростом и. В пределе, когда энергия колебаний становится равной энергии связи, дискретные уровни сливаются, и для энергий, превышающих энергию связи, получается сплошной спектр значений. Это означает, что при таких энергиях связь разрывается и атомы разлетаются с определенной относительной скоростью, соответствующей данному значению энергии в области сплошного спектра.
Существенный результат квантово-механических расчетов заключается в том, что в самом нижнем колебательном состоянии (v = 0) осциллятор обладает энергией так называемых нулевых
колебаний 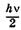 . Классическое же решение задачи допускает решения, соответствующие покоящемуся осциллятору с энергией, равной нулю: такое состояние отвечало бы наличию определенной координаты г0 и определенной скорости, равной нулю, что противоречит соотношениям неопределенностей.
. Классическое же решение задачи допускает решения, соответствующие покоящемуся осциллятору с энергией, равной нулю: такое состояние отвечало бы наличию определенной координаты г0 и определенной скорости, равной нулю, что противоречит соотношениям неопределенностей.
В биологии и медицине особенно важны представления об энергетических состояниях сложных органических молекул, содержащих двойные ковалентные связи между атомами углерода.
Одинарную связь между атомами углерода образуют s-электроны (s-связь), в ее формировании участвуют два электрона с противоположными спинами (спаренные электроны). Они формируют единое вытянутое электронное облако, симметричное относительно прямой, соединяющей центры атомов. На рис. 23.15, а показаны s-связи между атомами углерода в n-гексане. Области перекрывания заштрихованы, они находятся в промежутках между атомами, s-орбитали соседних одинарных связей не перекрываются друг с другом.
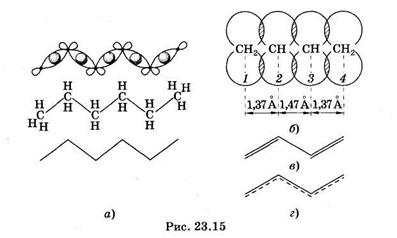
При возникновении между атомами углерода второй связи происходит перекрывание орбиталей еще двух электронов (р-орбиталей) соседних углеродных атомов. Их электронные облака имеют в сечении вид восьмерки, ось которой перпендикулярна направлению s-связи. Боковое перекрывание этих орбиталей в двух областях приводит к образованию молекулярной p-орбитали (рис. 23.15, б), соответственно электроны, формирующие p-орби-таль, называют p-электронами. Плотность образовавшегося облака л-электронов сосредоточена по обеим сторонам от линии s-связи. Она максимальна на расстоянии примерно 1 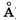 (10~10 м) от линии s-связи и обращается в нуль вблизи ядер атомов. Если двойные связи разделены одной одинарной (сопряжены), то происходит перекрывание p-орбиталей всех атомов углерода, участвующих в образовании цепочки сопряженных связей. На рис. 23.15, б показаны перекрывающиеся p-орбитали атомов углерода в молекуле бутадиена, одинарные s-связи условно изображены прямыми линиями, соединяющими атомы углерода. Данные о длине связей в молекуле бутадиена указывают на то, что при сопряжении двойных связей нет обычных двойных (длина связи
(10~10 м) от линии s-связи и обращается в нуль вблизи ядер атомов. Если двойные связи разделены одной одинарной (сопряжены), то происходит перекрывание p-орбиталей всех атомов углерода, участвующих в образовании цепочки сопряженных связей. На рис. 23.15, б показаны перекрывающиеся p-орбитали атомов углерода в молекуле бутадиена, одинарные s-связи условно изображены прямыми линиями, соединяющими атомы углерода. Данные о длине связей в молекуле бутадиена указывают на то, что при сопряжении двойных связей нет обычных двойных (длина связи
1,33 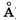 ) или одинарных (1,54
) или одинарных (1,54 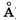 ) связей, связи являются примерно полуторными. Поэтому, хотя в органической химии и принято изображать систему сопряженных двойных связей, как показано на рис. 23.15, в, более точно ситуацию отображает рис. 23.15, г. Каждый электрон, участвующий в образовании двойной связи, оказывается принадлежащим не какой-то определенной паре атомов углерода, а сразу всей цепочке атомов, связанных сопряженными связями. Такие p-электроны делокализованы по всей цепочке и могут свободно по ней перемещаться подобно электронам проводимости в металле, но не могут ее покинуть. Другими словами электроны p-орбиталей находятся в потенциальной яме. Можно показать, что энергия этих электронов квантована, подобно энергии электронов в атоме.
) связей, связи являются примерно полуторными. Поэтому, хотя в органической химии и принято изображать систему сопряженных двойных связей, как показано на рис. 23.15, в, более точно ситуацию отображает рис. 23.15, г. Каждый электрон, участвующий в образовании двойной связи, оказывается принадлежащим не какой-то определенной паре атомов углерода, а сразу всей цепочке атомов, связанных сопряженными связями. Такие p-электроны делокализованы по всей цепочке и могут свободно по ней перемещаться подобно электронам проводимости в металле, но не могут ее покинуть. Другими словами электроны p-орбиталей находятся в потенциальной яме. Можно показать, что энергия этих электронов квантована, подобно энергии электронов в атоме.
Представим, что сопряженная цепь состоит из N звеньев, включающих по одной двойной и одной одинарной связи, тогда общая длина цепи равна
I = NL, (23.43)
где L — длина одного звена. Квантование энергий p-орбиталей является следствием волновых свойств электронов (23.2). Электрон (волна) перемещается по потенциальной яме длиной I со скоростью v, не выходя за ее пределы. Внутри ямы вся энергия электрона кинетическая, на краях ямы — потенциальная. Волна будет устойчива, если внутри ямы укладывается целое число п полуволн, т. е. если волна будет стоячей с узлами на стенках
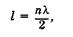 (23.44)
(23.44)
где л = 1, 2,3, ... ит. д. Подставив l, из формулы для длины волны де Бройля (23.2) в (23.44), находим возможные значения скорости электрона
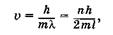
при этом его кинетическая энергия равна
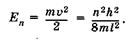 (23.45)
(23.45)
Видно, что формула (23.45) совпадает с (23.19), полученной при решении уравнения Шредингера для частицы в бесконечно глубокой потенциальной яме. Таким образом, энергия p-орбиталей квантована и может иметь только дискретные значения 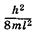 ,
,
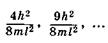 . Согласно принципу Паули на каждом уровне
. Согласно принципу Паули на каждом уровне
энергии могут находиться только два электрона с противоположными спинами. Следовательно, в основном (невозбужденном) состоянии 2N электронов p-орбиталей и p-членной цепи занимают N уровней с наименьшими значениями энергии от 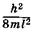 до
до 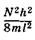
Молекулярные орбитали с энергиямии
и 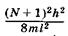 выше в основном состоянии молекулы будут оставаться свободными.
выше в основном состоянии молекулы будут оставаться свободными.
При поглощении квантов света может произойти переход какого-либо электрона с заполненного на свободный уровень. Молекула при этом оказывается в электронно-возбужденном состоянии. Кванты оптического (ультрафиолетового или видимого) излучения способны обычно вызывать электронные переходы только с верхнего заполненного (n = N) на нижний (n = N + 1) или следующий (n = N + 2) свободные уровни. Поэтому в оптической спектроскопии на схемах молекулярных энергетических уровней (рис. 23.16) изображают только верхний заполненный и нижние свободные уровни, тогда как нижние заполненные уровни не приводят совсем.
На рис. 23.16 представлена схема Яблонского энергетических уровней молекул с сопряженными связями, жирными горизонтальными линиями показаны электронные уровни, тонкими — колебательные, вращательные уровни не приведены. Рядом с уровнями в прямоугольных рамках схематически представлены основные и возбужденные состояния молекулы, стрелками показано направление спинов электронов. Состояния молекул, при которых спины имеют противоположное направление и сумма спиновых квантовых чисел равна нулю, называются синглетными и обозначаются буквами S с индексом внизу. Верхний заполненный уровень обозначают So, а свободные — S1 S2 и т. д. В электронно-возбужденных молекулах у электронов на уровнях S1 S2 и т. д. может произойти обращение спина, тогда молекула оказывается в триплетном возбужденном состоянии, обозначаемом T1 T2 и т. д. Сумма
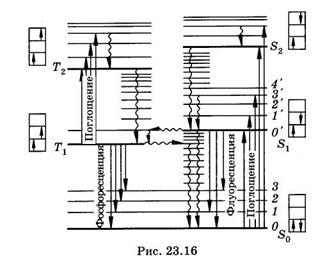
спиновых квантовых чисел молекул в триплетных состояниях равна единице1. Каждому возбужденному синглетному уровню соответствует один триплетный. По принципу Паули уровень То, соответствующий So, не существует, т. е. невозбужденная молекула не может быть в триплетном состоянии. Переходы между молекулярными энергетическими уровнями будут обсуждаться в главе 24.
______________________________
1 Не следует смешивать это обозначение с названием электронного слоя L и с символом полного момента импульса электрона.
ГЛАВА 24
Излучение и поглощение энергии атомами и молекулами
Огромное количество разных явлений происходит потому, что изменяется энергия атомов и молекул. Во многих случаях эффективное использование явления для практики оказывается возможным только с непременным учетом его молекулярной (атомной) природы.
В этой главе излагаются особенности излучения и поглощения энергии атомами и молекулами, а также некоторые практически важные явления, знание молекулярной природы которых существенно для их использования. Некоторые вопросы этой обширной темы рассматриваются в следующей главе.
§ 24.1. Поглощение света
Интенсивность света, распространяющегося в среде, может уменьшаться из-за поглощения и рассеяния его молекулами (атомами) вещества.
Поглощением света называют ослабление интенсивности света при прохождении через любое вещество вследствие превращения световой энергии в другие виды энергии.
 Поглощение кванта света происходит при его неупругом столкновении с молекулой (атомом), приводящем к передаче энергии фотона веществу, и является случайным событием. Вероятность поглощения кванта света образцом вещества толщиной l (рис. 24.1) оценивается величиной коэффициента поглощения 1-Т, равного отношению интенсивностей поглощенного света 1П = 10 - I к интенсивности падающего /0
Поглощение кванта света происходит при его неупругом столкновении с молекулой (атомом), приводящем к передаче энергии фотона веществу, и является случайным событием. Вероятность поглощения кванта света образцом вещества толщиной l (рис. 24.1) оценивается величиной коэффициента поглощения 1-Т, равного отношению интенсивностей поглощенного света 1П = 10 - I к интенсивности падающего /0
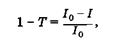 (24.1)
(24.1)
где / — интенсивность прошедшего света, Т =I/I0 коэффициент пропускания.
Выведем закон поглощения света веществом. Выделим тонкий слой вещества dx, перпендикулярный пучку монохроматического света интенсивностью i (I0 > i > I), и будем исходить из предположения, что ослабление света (доля поглощенных квантов) -di/i таким слоем не зависит от интенсивности (если интенсивность не слишком велика), а определяется только толщиной слоя dx и коэффициентом пропорциональности 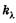 :
:
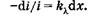 (24.2)
(24.2)
Коэффициент 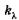 различен для разных длин волн и его величина зависит от природы вещества. Интегрируя (24.2) и подставив пределы интегрирования для х от 0 до I и для i от I0 до I, получаем
различен для разных длин волн и его величина зависит от природы вещества. Интегрируя (24.2) и подставив пределы интегрирования для х от 0 до I и для i от I0 до I, получаем
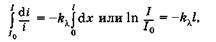
откуда, потенцируя, имеем
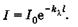 (24.3)
(24.3)
Эта формула выражает закон поглощения света Бугера. Коэффициент 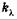 называют натуральным показателем поглощения, его величина обратна расстоянию, на котором интенсивность света ослабляется в результате поглощения в среде в е раз.
называют натуральным показателем поглощения, его величина обратна расстоянию, на котором интенсивность света ослабляется в результате поглощения в среде в е раз.
Так как поглощение света обусловлено взаимодействием с молекулами (атомами), то закон поглощения можно связать с некоторыми характеристиками молекул. Пусть п — концентрация молекул (число молекул в единице объема), поглощающих кванты света. Обозначим буквой s эффективное сечение поглощения молекулы — некоторую площадь, при попадании фотона в которую происходит его захват молекулой. Другими словами молекулу можно представить как мишень определенной площади.
Если считать, что площадь сечения прямоугольного параллелепипеда (рис. 24.1) равна S, то объем выделенного слоя Sdx, а количество молекул в нем nSdx; суммарное эффективное сечение всех молекул в этом слое будет snSdx. Доля площади поперечного сечения поглощения всех молекул в общей площади сечения
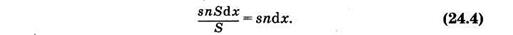
откуда после интегрирования и потенцирования имеем
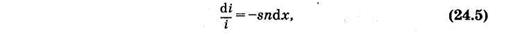
Можно считать, что такая же, как и (24.4), часть попавших на слой квантов поглощается молекулами, ибо отношение площадей определяет вероятность взаимодействия одного кванта с молекулами выделенного слоя. Доля поглощенных слоем квантов равна относительному уменьшению интенсивности (di/i) света. На основании изложенного можно записать 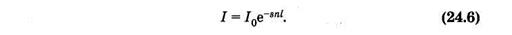
В это уравнение, аналогичное (24.3), входит параметр s, который отражает способность молекул поглощать монохроматический свет используемой длины волны.
Более приняты молярные концентрации С = n/NA, откуда п=CNA. Преобразуем произведение sn = sCNA = XlC, где Xl= sNA — натуральный молярный показатель поглощения. Его физический смысл — суммарное эффективное сечение поглощения всех молекул одного моля вещества. Если молекулы, поглощающие кванты, находятся в растворителе, который не поглощает свет, то можно (24.6) записать в виде
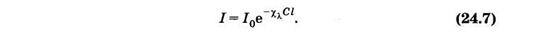
Эта формула выражает закон Бугера—Ламберта—Бера. Влабораторной практике этот закон обычно выражают через показательную функцию с основанием 10:
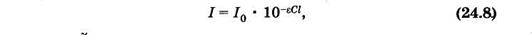
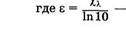
молярный показатель поглощения2.
 Закон Бугера—Ламберта—Бера используют для фотометрического определения концентрации окрашенных веществ. Для этого непосредственно измеряют потоки падающего и прошедшего через раствор монохроматического света (концентрационная колориметрия), однако определенный таким образом коэффициент пропускания Т (или поглощения 1 - Т, см. (24.1)) неудобен, так как он из-за вероятностного характера процесса3 связан с концентрацией нелинейно [см. (24.8) и рис. 24.2, а]. Поэтому в количественном анализе обычно определяют оптическую плотность (D) раствора3,
Закон Бугера—Ламберта—Бера используют для фотометрического определения концентрации окрашенных веществ. Для этого непосредственно измеряют потоки падающего и прошедшего через раствор монохроматического света (концентрационная колориметрия), однако определенный таким образом коэффициент пропускания Т (или поглощения 1 - Т, см. (24.1)) неудобен, так как он из-за вероятностного характера процесса3 связан с концентрацией нелинейно [см. (24.8) и рис. 24.2, а]. Поэтому в количественном анализе обычно определяют оптическую плотность (D) раствора3,
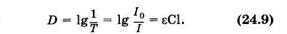
представляющую десятичный логарифм величины, обратной коэффициенту пропускания,
Оптическая плотность удобна тем, что она линейно связана с концентрацией определяемого вещества (рис. 24.2, б).
Закон Бугера—Ламберта—Бера выполняется не всегда. Он справедлив при следующих предположениях: 1) используется монохроматический свет; 2) молекулы растворенного вещества в растворе распределены равномерно; 3) при изменении концентрации характер
взаимодействия между растворенными молекулами не меняется (иначе фотофизические свойства вещества, в том числе и значения she, будут изменяться); 4) в процессе измерения не происходят химические превращения молекул под действием света; 5) интенсивность падающего света должна быть достаточно низка (чтобы концентрация невозбужденных молекул практически не уменьшалась в ходе измерения). Зависимости s, %, е или D от длины волны света называют спектрами поглощения вещества.
Спектры поглощения являются источниками информации о состоянии вещества и о структуре энергетических уровней атомов и молекул (см. § 24.3 и 24.4). Спектры поглощения используют для качественного анализа растворов окрашенных веществ.

1 Так как результирующий спиновый момент равен единице, то в магнитном поле происходит расщепление энергетического уровня на три (см. § 25.1), отсюда и термин «триплетный» уровень. Триплетные состояния молекул были открыты А. Н. Терениным в 1943 г.
2 В спектроскопии e принято называть молярным коэффициентом поглощения.
3 Экспоненциальная зависимость интенсивности прошедшего светаот концентрации вещества (24.6—24.8) определяется вероятностным характером поглощения квантов света. Доля поглощенных квантов di/I (24.5) может рассматриваться как вероятность поглощения, зависящая от суммарной площади поглощающих кванты мишеней в тонком слое образца sndx (24.5). Попадание или непопадание кванта в мишень — случайный, вероятностный процесс. Аналогичные экспоненциальные зави-
симости, отражающие вероятностный характер процессов, получаются при выводе уравнений, описывающих распределение Больцмана (§ 2.4), ослабление рентгеновского излучения веществом (§ 26.3) или радиоактивный распад (§ 27.2).
4 В англоязычной литературе сейчас вместо оптической плотности используется другое обозначение и термин: поглощательная способность
(A) (absorbance).
§ 24.2. Рассеяние света
Рассеянием света называют явление, при котором распространяющийся в среде световой пучок отклоняется по всевозможным направлениям.
Необходимое условие для возникновения рассеяния света — наличие оптических неоднородностей, т. е., в частности, областей с иным, чем основная среда, показателем преломления.
Рассеяние света возникает на оптических неоднородностях среды. Различают два основных вида таких неоднородностей:
1) 1) мелкие инородные частицы в однородном прозрачном веществе. Такие среды являются мутными: дым (твердые частицы в газе), туман (капельки жидкости в газе), взвеси, эмульсии и т. п. Рассеяние в мутных средах называют явлением Тиндаля;
2) 2) оптические неоднородности, возникающие в чистом веществе из-за статистического отклонения молекул от равномерного распределения (флуктуации плотности). Рассеяние света на неоднородностях этого типа называют молекулярным, например рассеяние света в атмосфере.
Уменьшение интенсивности света вследствие рассеяния, как и при поглощении, описывают показательной функцией
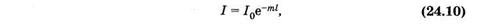
где m — показатель рассеяния (натуральный).
При совместном действии поглощения и рассеяния света ослабление интенсивности также является показательной функцией
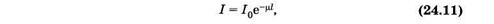
где m — показатель ослабления (натуральный). Как нетрудно видеть, m = m + kl.

Рэлей установил, что при рассеянии в мутной среде на неоднородностях, приблизительно меньших 0,2l (l — длина волны света), а также при молекулярном рассеянии интенсивность рассеянного света обратно пропорциональна четвертой степени длины волны (закон Рэлея):

Это означает, что из белого света веществом, например в точке Д (рис. 24.3), будут преимущественно рассеиваться голубые и фиолетовые лучи (направление А), а красные — проходить в направлении Б падающего света. Аналогичное явление наблюдается и в природе: голубой цвет неба — рассеянный свет, красный цвет заходящего Солнца — изменение спектра белого света из-за значительного рассеяния голубых и фиолетовых лучей в толще атмосферы при наклонном падении (см. пояснение к рис. 22.3).
Меньшее рассеяние красных лучей используют в сигнализации: опознавательные огни на аэродромах, наиболее ответственный свет светофора — красный, и т. п. Инфракрасные лучи рассеиваются еще меньше. На рис. 24.4 изображены две фотографии пейзажа: на левой, снятой обычным методом, туман сильно ограничил видимость; на правой, снятой в инфракрасном излучении на специальной пластинке, туман не мешает, он оказался прозрачным для более длинных волн.
Дата добавления: 2015-06-22; просмотров: 927;
