Поток солнечной радиации, приходящийся на 1 м2 площади границы земной атмосферы, составляет 1350 Вт. Эту величину называют солнечной постоянной. 2 страница
В рамках геометрической электронной оптики возможно, в частности, описание движения заряженных частиц в электрическом и магнитном полях, а также схематическое построение изображения в электронном микроскопе (см. рис. 23.2, б).
Подход волновой электронной оптики важен в том случае, когда проявляются волновые свойства заряженных частиц. Хорошей иллюстрацией этому является нахождение разрешающей способности (предела разрешения) электронного микроскопа, приведенное в начале параграфа.
§ 23.3. Волновая функция и её физический смысл
Так как с микрочастицей сопоставляют волновой процесс, который соответствует ее движению, то состояние частиц в квантовой механике описывается волновой функцией, зависящей от координат и времени: 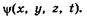 Эта функция аналогична функции s (см. § 5.7), описывающей волновой процесс в механике.
Эта функция аналогична функции s (см. § 5.7), описывающей волновой процесс в механике.
Если силовое поле, действующее на частицу, является стационарным, т. е. не зависящим от времени, то 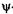 -функцию можно представить в виде произведения двух сомножителей, один из которых зависит от времени, а другой — от координат:
-функцию можно представить в виде произведения двух сомножителей, один из которых зависит от времени, а другой — от координат:
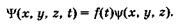 (23.5)
(23.5)
В дальнейшем будем рассматривать только стационарные состояния; y-функция координат является вероятностной характеристикой пространственной локализации частицы. Поясним смысл этого утверждения.
Выделим в пространстве достаточно малый объем dV = dxdydz, в пределах которого значения 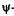 функции можно считать одинаковыми. Вероятность нахождения dWB частицы в этом объеме пропорциональна объему и определяется, согласно М. Борну, квадратом модуля y-функции:
функции можно считать одинаковыми. Вероятность нахождения dWB частицы в этом объеме пропорциональна объему и определяется, согласно М. Борну, квадратом модуля y-функции:
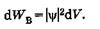 (23.6)
(23.6)
Отсюда следует физический смысл волновой функции:
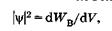 (23.7)
(23.7)
 т. е. квадрат модуля волновой функции равен плотности вероятности, или отношению вероятности нахождения частицы в малом объеме dV к этому объему.
т. е. квадрат модуля волновой функции равен плотности вероятности, или отношению вероятности нахождения частицы в малом объеме dV к этому объему.
Интегрируя выражение (23.6) по некоторому объему V, находим вероятность нахождения частицы в этом объеме:
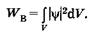 (23.8)
(23.8)
Отсюда получаем условие нормировки волновой функции в виде 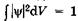 , где интегрирование ведется по всему бесконечному пространству, вероятность нахождения в котором частицы равна единице.
, где интегрирование ведется по всему бесконечному пространству, вероятность нахождения в котором частицы равна единице.
§ 23.4. Соотношения неопределенностей
Одним из важных положений квантовой механики являются соотношения неопределенностей, предложенные В. Гейзенбергом. Существуют различные пары физических величин (называемые канонически сопряженными переменными), которые могут быть одновременно определены лишь с ограниченной точностью.
Пусть одновременно измеряют положение и импульс частицы, при этом неопределенности в измерении координаты и проекции импульса на эту координатную ось, например х, равны соответственно 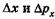
В классической физике нет каких-либо ограничений, запрещающих с любой степенью точности одновременно измерить как одну, так и другую величину, т. е. 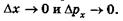
В квантовой механике положение принципиально иное: Dх и Dрх, соответствующие одновременному определению х и рх, связаны зависимостью
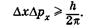 (23.9)
(23.9)
Таким образом, чем точнее определена координата
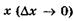 ,
,
тем менее точно определена соответствующая проекцияим- импульса 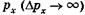 , и наоборот. Аналогично для у и г:
, и наоборот. Аналогично для у и г:
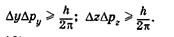 (23.10)
(23.10)
Формулы (23.9), (23.10) называют соотношениями неопределенностей для координат и импульсов. Вычисления, проделанные для электрона, показывают, что его локализация внутри атомного ядра невозможна, т. к. в этом случае неопределенность его скорости должна превысить величину скорости света. Действительно, если 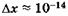 м (размер ядра атома), то из (23.9) следует, что величина Apv должна превысить
м (размер ядра атома), то из (23.9) следует, что величина Apv должна превысить 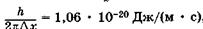 , следовательно, неопределенность скорости
, следовательно, неопределенность скорости 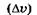 электрона
электрона 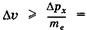
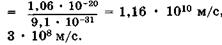 , тогда как скорость света равна
, тогда как скорость света равна
Еще одной парой канонически сопряженных переменных являются энергия частицы Е и время t. Соотношение неопределенностей для этих переменных имеет вид
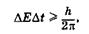 (23.11)
(23.11)
где 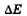 — неопределенность энергии некоторого состояния системы,
— неопределенность энергии некоторого состояния системы, 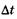 — время его существования. Соотношение (23.11) означает, что чем короче время существования какого-либо состояния системы, тем больше неопределенность значения энергии этого состояния. Энергетические уровни (дискретные значения энергии) E1 Е2 и т. д. имеют некоторую ширину (рис. 23.4), зависящую от времени пребывания (времени жизни) системы в состояниях, соответствующих этим уровням энергии.
— время его существования. Соотношение (23.11) означает, что чем короче время существования какого-либо состояния системы, тем больше неопределенность значения энергии этого состояния. Энергетические уровни (дискретные значения энергии) E1 Е2 и т. д. имеют некоторую ширину (рис. 23.4), зависящую от времени пребывания (времени жизни) системы в состояниях, соответствующих этим уровням энергии.
«Размытость» уровней приводит к неопределенности энергии излучаемого фотона 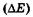 и его частоты
и его частоты 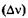 при переходе системы с одного энергетического уровня на другой:
при переходе системы с одного энергетического уровня на другой:
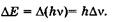 (23.12)
(23.12)
Это экспериментально проявляется в уширении спектральных линий.
§ 23.5. Уравнение Шредингера.
Электрон в потенциальной яме
Так как состояние микрочастицы описывают 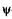 -функцией, то надо указать способ нахождения этой функции с учетом внешних условий. Это возможно в результате решения основного уравнения квантовой механики, предложенного Э. Шредингером (1926). Такое уравнение в квантовой механике постулируется так же, как в классической механике постулируется второй закон Ньютона.
-функцией, то надо указать способ нахождения этой функции с учетом внешних условий. Это возможно в результате решения основного уравнения квантовой механики, предложенного Э. Шредингером (1926). Такое уравнение в квантовой механике постулируется так же, как в классической механике постулируется второй закон Ньютона.
Применительно к стационарным состояниям частицы уравнение Шредингера может быть записано так:
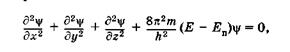 (23.13)
(23.13)
где т — масса частицы, Е и Еп — ее полная и потенциальная энергии (потенциальная энергия определяется силовым полем, в котором находится частица, и для стационарного случая не зависит от времени).
Если частица перемещается только вдоль некоторой линии, например, вдоль оси ОХ (одномерный случай), то уравнение Шредингера существенно упрощается и принимает вид
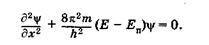 (23.14)
(23.14)
Одним из наиболее простых примеров использования уравнения Шредингера является решение задачи о движении частицы в одномерной «потенциальной яме».
Пусть электрон перемещается вдоль оси ОХ только в пределах О < х < I (рис. 23.5). Это означает, что в указанном интервале y-функция отлична от нуля, а вне интервала (х < =0, х >= I) равна нулю. Так какна частицу в выделенном интервале 0 < х < I силовые поля не действуют, то ее потенциальная энергия может иметь любое постоянное значение (наиболее удобно принять Еп = 0). Вне этого интервала электрона нет, т. е. электрон не может выйти за пределы интервала, поэтому в области х <= 0 и х >= I следует счи  тать его потенциальную энергию бесконечно большой, а волновую функцию равной нулю (y = 0). На рис. 23.5 показана графическая зависимость En = f(x). Интервал 0 < х < I, удовлетворяющий сформулированным выше условиям, называют одномерной прямоугольной потенциальной ямой с бесконечно высокими стенками. С учетом ЕП = 0 уравнение Шредингера (23.14) для интервала 0 < х < I имеет вид
тать его потенциальную энергию бесконечно большой, а волновую функцию равной нулю (y = 0). На рис. 23.5 показана графическая зависимость En = f(x). Интервал 0 < х < I, удовлетворяющий сформулированным выше условиям, называют одномерной прямоугольной потенциальной ямой с бесконечно высокими стенками. С учетом ЕП = 0 уравнение Шредингера (23.14) для интервала 0 < х < I имеет вид
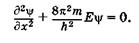 (23.14а)
(23.14а)
Произведя замену
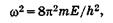 (23.15)
(23.15)
получим
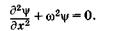 (23.16)
(23.16)
Это уравнение аналогично дифференциальному уравнению гармонического колебания (см. § 5.1), решение (5.8) которого запишем в виде
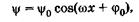 (23.17)
(23.17)
где y0 — амплитуда волновой функции, 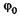 — ее начальная фаза.
— ее начальная фаза.
Чтобы найти две постоянные 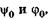 а также возможные зна-
а также возможные зна-
чения w или E, рассмотрим граничные условия с учетом непрерывности волновой функции y на границах интервала:
1) 1) при х = 0, 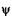 =0;
=0;
2) 2) при х = I, 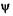 = 0.
= 0.
Подставляя эти значения в (23.17), получаем 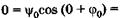
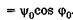 , Физический смысл здесь имеет только одно значение:
, Физический смысл здесь имеет только одно значение:
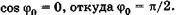
С учетом 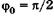 из (23.17) имеем
из (23.17) имеем 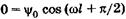 . Физический смысл здесь имеет только одно значение:
. Физический смысл здесь имеет только одно значение: 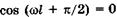 , или
, или 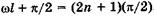 , откуда
, откуда
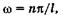 (23.18)
(23.18)
где п — целое число, оно принимает значения 1, 2, 3, ...; п # 0, так как в противном случае 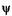 = 0 при любом х, что означает отсутствие электрона в потенциальной яме. Число п называют квантовым числом. Из (23.15) находим энергию
= 0 при любом х, что означает отсутствие электрона в потенциальной яме. Число п называют квантовым числом. Из (23.15) находим энергию 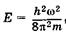 , что с учетом (23. 18) дает
, что с учетом (23. 18) дает
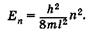 (23.19)
(23.19)
Индекс п при Е показывает, что различным значениям квантового числа п соответствует и разная энергия.
Подставляя со из (23.18) в (23.17) и учитывая 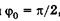 , получаем
, получаем
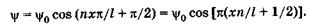 (23.20)
(23.20)
Проанализируем выражения (23.19) и (23.20). Прежде всего примечательно, что решение уравнения Шредингера для электрона в потенциальной яме без каких-либо дополнительных постулатов приводит к дискретным, квантованным значениям энергии:
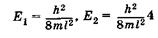 и т. д.
и т. д.
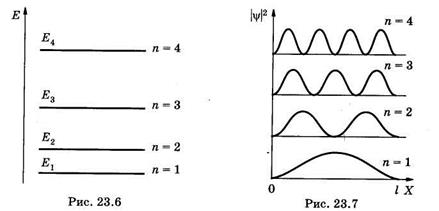
Энергетические уровни E1 E2, E3, E4, соответствующие разным Состояниям электрона, схематически показаны на рис. 23.6. Вычислим разность энергий соседних уровней га + 1и га:
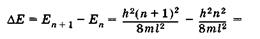
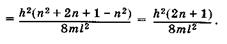 (23.21)
(23.21)
Из (23.21) видно, что при некотором фиксированном значении га дискретность, т. е. различие энергий соседних уровней тем меньше, чем больше размеры потенциальной ямы. Так, например, рассмотри два случая при га = 1:
|
Возведя (23.20) в квадрат, получим плотность вероятности нахождения электрона в разных точках потенциальной ямы. 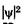 На рис. 23.7 показана графическая зависимость от х при разных дискретных состояниях, т. е. разных квантовых
На рис. 23.7 показана графическая зависимость от х при разных дискретных состояниях, т. е. разных квантовых  числах. Как видно из рисунка, электрон может с разной вероятностью находиться в разных местах потенциальной ямы. Есть такие точки, в кото-
числах. Как видно из рисунка, электрон может с разной вероятностью находиться в разных местах потенциальной ямы. Есть такие точки, в кото-

рых вероятность нахождения электрона вообще равна нулю. Это существенно отличается от представлений классической физики, согласно которым нахождение частицы в разных местах потенциальной ямы равновероятно (рис. 23.8), т. е. невозможно разделение ямы точками, в которых исключено нахождение частицы. Уравнение Шредингера можно применить и к более сложным силовым полям, например, к электрону в атоме. Это приведет к дополнительным математическим трудностям, но не изменит основных особенностей атомных систем: дискретности энергетических состояний, вероятностных суждений о нахождении электрона, своеобразной зависимости |\|/|2 от координат и т. д.
§ 23.6. Применение уравнения Шредингера к атому водорода. Квантовые числа
Описание состояний атомов и молекул с помощью уравнения Шредингера является достаточно сложной задачей. Наиболее просто она решается для одного электрона, находящегося в поле ядра. Такие системы соответствуют атому водорода и водородопо-добным ионам (однократно ионизированный атом гелия, двукратно ионизированный атом лития и т. п.). Однако и в этом случае решение задачи выходит за рамки нашего курса, поэтому ограничимся лишь качественным изложением вопроса.
Прежде всего в уравнение Шредингера (23.13) следует подставить потенциальную энергию, которая для двух взаимодействующих точечных зарядов -е (электрон) и Ze (ядро), находящихся на расстоянии г в вакууме, выражается следующим образом:
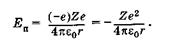 (23.22)
(23.22)
При центральной симметрии поля, созданного ядром, удобнее решать задачу не в декартовых прямоугольных координатах, а в сферических 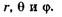
Решение уравнения Шредингера находят в виде произведения
функций:
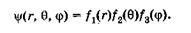 (23.23)
(23.23)
Аналогично тому, как для электрона в прямоугольной потенциальной яме с бесконечно высокими стенками граничные условия привели к конкретным возможным значениям функции у и энергии Еп, так и в потенциальной яме, соответствующей атому водорода, физические условия приводят к определенным типам функций fv f2, f3 и, следовательно, y-функции. Здесь также проявляется главная особенность квантово-механических систем — дискретность физических величин.
 Дискретность математически проявляется в том, что любой из функций, являющейся решением уравнения Шредингера с заданными граничными условиями и потенциальной энергии Еп, соответствует набор (спектр) целочисленных значений параметров, каждому из которых отвечает так называемое квантовое число. В отличие от прямоугольной потенциальной ямы с бесконечно высокими стенками состояние электрона в атоме водорода характеризуется не одним, а несколькими квантовыми числами. Решением уравнения Шредингера вводятся три квантовые числа: п, l, тl В общем случае квантовыми числами называют целые (0, ±1, ±2, ...) или полуцелые (+1/2, ±3/2, ±5/2…) числа, определяющие возможные дискретные значения физических величин, которые характеризуют квантовые системы.
Дискретность математически проявляется в том, что любой из функций, являющейся решением уравнения Шредингера с заданными граничными условиями и потенциальной энергии Еп, соответствует набор (спектр) целочисленных значений параметров, каждому из которых отвечает так называемое квантовое число. В отличие от прямоугольной потенциальной ямы с бесконечно высокими стенками состояние электрона в атоме водорода характеризуется не одним, а несколькими квантовыми числами. Решением уравнения Шредингера вводятся три квантовые числа: п, l, тl В общем случае квантовыми числами называют целые (0, ±1, ±2, ...) или полуцелые (+1/2, ±3/2, ±5/2…) числа, определяющие возможные дискретные значения физических величин, которые характеризуют квантовые системы.
Первое из них — главное квантовое число п = 1,2,3, ... . Оно определяет уровни энергии электрона в атоме водорода (z = 1) или водородоподобных ионах:
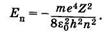
(23.24)
Это выражение вытекает из решения уравнения Шредингера и полностью совпадает с соответствующей формулой теории Бора (см. §23.7).
На рис. 23.9 штриховыми прямыми показаны уровни возможных значений полной энергии Е электронов в атоме водорода (E1 Е2, Е3 и т. д.) и график зависимоcти потенциальной энергии Еп от расстояния rмежду электроном и ядром [см. (23.22)]. С возрастанием главного квантового числа га увеличивается r [см., например, (23.33)],
а полная [см. (23.24)] и потенциальная энергии стремятся к нулю. Кинетическая энергия также стремится к нулю. Заштрихованная область (Е > 0) — непрерывный спектр значений энергии — соответствует состоянию свободного электрона.
Второе квантовое число — орбитальное квантовое число I, которое при данном п может принимать значения 0, 1, 2, ..., п — 1. Это число характеризует орбитальный момент импульса Ll электрона относительно ядра:
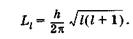 (23.25)
(23.25)
Третье квантовое число — магнитное квантовое число тг, которое при данном l принимает значения 0, ±1, +2, ..., ±1, всего 21 + 1 значений. Это число определяет проекции орбитального момента импульса электрона на некоторое произвольно выбранное направление Z (или направление внешнего магнитного поля):
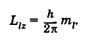 (23.26)
(23.26)
Четвертое квантовое число — спиновое {магнитное спиновое)1 квантовое число m8. Оно может принимать только два значения (±1/2) и характеризует возможные значения проекции на ось Z спина (собственного механического момента) электрона:
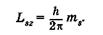 (23.27)
(23.27)
Состояния электрона в атоме с заданными п и I обозначают следующим образом: Is, 2s, 2p, 3s и т. д. Здесь цифра указывает значение главного квантового числа, а буква — орбитальное квантовое число: символам s, p, d, f, ... соответствуют значения I =0, 1, 2, 3 и т. д. (табл. 30).
Число состояний с заданными п и I равно 2(2l + 1). Чтобы найти общее число состояний, имеющих одинаковое главное квантовое число, просуммируем 2(2l + 1) по всем возможным значениям l от l = 0 до l = п - 1:
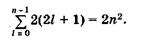 (23.28)
(23.28)
Таким образом, первому уровню энергии атома водорода соответствуют два состояния электрона, второму — 8, третьему — 18 и т. д. (см. табл. 30).
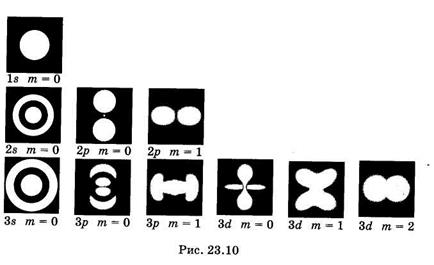
Наглядное представление о нахождении электрона в атоме дает фотомодель электронного облака (рис. 23.10). Снимки выполнены на модели со светящейся лампочкой. Рассчитав плотности вероятности 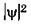 нахождения электрона в атоме в состояниях с разными значениями п, l и ml лампочку перемещали в соответствии с этим расчетом: больше времени она находилась в местах с большей плотностью вероятности, менее длительно — в местах с меньшей плотностью вероятности. В результате экспозиции на фотопленке получились места разной освещенности, которые иллюстрируют распределение вероятности нахождения электрона в атоме. Из рисунков видно, сколь условно и даже неверно понятие «орбита» применительно к движению электрона.
нахождения электрона в атоме в состояниях с разными значениями п, l и ml лампочку перемещали в соответствии с этим расчетом: больше времени она находилась в местах с большей плотностью вероятности, менее длительно — в местах с меньшей плотностью вероятности. В результате экспозиции на фотопленке получились места разной освещенности, которые иллюстрируют распределение вероятности нахождения электрона в атоме. Из рисунков видно, сколь условно и даже неверно понятие «орбита» применительно к движению электрона.
Спиновый и орбитальный магнитные моменты взаимодействуют между собой, это изменяет систему энергетических уровней атома по сравнению с той, которая была бы без такого взаимодействия. Спин-орбитальное взаимодействие приводит к расщеплению энергетических уровней и тонкой структуре спектральных линий излучения. Если это расщепление уровней существенно, то необходимо учитывать полный момент импульса электрона — орбитальный плюс спиновый. При этом вместо тп1 и ms используют другие квантовые числа: j и тj
Квантовое число j определяет дискретные значения полного момента импульса Lj. электрона:
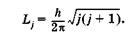 (23.29)
(23.29)
При заданном l квантовое число у принимает два значения: 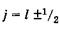
Таблица 30
i 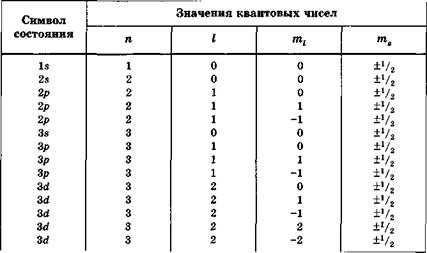
Магнитное квантовое число т, характеризует возможные проекции полного момента импульса электрона Lj. на некоторое произвольно выбранное направление Z, либо направление внешнего магнитного поля:
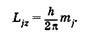 (23.30)
(23.30)
При заданном у квантовое число тj, принимает 2j + 1 значений: -j, -j + 1, ..., + j.
______________________
1 Наличие спина у частиц и спинового квантового числа не следует из уравнения Шредингера.
§ 23.7. Понятие о теории Бора
Еще до создания квантовой механики датский физик Н. Бор в 1913 г. предложил теорию атома водорода и водородоподобных ионов, которая основывалась на планетарной модели атома и двух постулатах. Постулаты Бора не укладывались в рамки классической физики.
Согласно первому постулату, атом и атомные системы могут длительно пребывать только в определенных стационарных состояниях. Находясь в таких состояниях, атом не излучает и не поглощает энергии. Стационарным состояниям соответствуют дискретные значения энергии: E1 Е2, …..•
Любое изменение энергии атома или атомной системы связано со скачкообразным переходом из одного стационарного состояния в другое.
По второму постулату, при переходе атома из одного состояния в другое атом испускает или поглощает фотон частоты v, энергия которого определяется разностью энергий Еj, Ek атомных состояний:
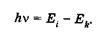 (23.31)
(23.31)
Переход из состояния с большей энергией в состояние с меньшей энергией сопровождается излучением фотона. Обратный процесс происходит при поглощении фотона.
Согласно теории Бора, электрон в атоме водорода вращается по круговой орбите вокруг ядра. Из всех возможных орбит стационарные состояния соответствуют только тем, для которых момент импульса (орбитальный механический момент) равен целому числу 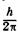 :
:
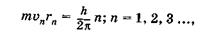 (23.32)
(23.32)
где т — масса электрона, 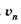 — его скорость на я-й орбите, rn— ее радиус.
— его скорость на я-й орбите, rn— ее радиус.
На электрон, вращающийся по круговой орбите в атоме (ионе), действует кулоновская сила притяжения со стороны положительно заряженного ядра, которая, по второму закону Ньютона, равна произведению массы электрона на центростремительное ускорение (запись дана для вакуума):
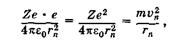 (23.33)
(23.33)
где е — заряд электрона, Ze — заряд ядра. Для водорода Z = 1, для водородоподобных ионов Z > 1. Исключая v n из (23.32) и (23.33), получаем
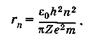 (23.34)
(23.34)
Используя (23.33), находим кинетическую энергию электрона:
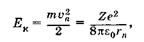 (23.35)
(23.35)
а сумма кинетической (23.35) и потенциальной (23.22) энергий дает полную энергию электрона:
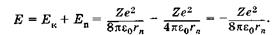 (23.36)
(23.36)
Подставляя выражение (23.34) в (23.36), получаем дискретные значения энергии 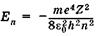 , как в квантово-механическом описании атомов (23.24).
, как в квантово-механическом описании атомов (23.24).
На основании второго постулата (23.31) и формулы (23.24) Бор получил формулу (24.14), объясняющую сериальные закономерности спектра атома водорода и водородоподобных ионов (см. § 24.3).
Теория Бора в свое время явилась триумфом развития атомной физики. Впервые, хотя и для простейшей атомной системы (один электрон вращается вокруг ядра), были раскрыты закономерности спектров.
Несмотря на большой успех теории Бора, скоро стали заметны и ее недостатки. Так, в рамках этой теории не удалось объяснить различия интенсивностей спектральных линий, т. е. ответить на вопрос, почему одни переходы между энергетическими уровнями более вероятны, чем другие. Теория Бора не раскрыла спектральных закономерностей более сложных атомных систем, в частности, атома гелия (с двумя электронами, вращающимися вокруг ядра).
Недостатком теории Бора была ее внутренняя противоречивость. Эта теория объединяла в себе положения принципиально отличных теорий: классической и квантовой физики. Так, например, в соответствии с теорией Бора считается, что электрон в атоме движется по определенным орбитам (классические представления), но при этом не излучает и не поглощает электромагнитной энергии (противоречит классической электродинамике).
В первой четверти двадцатого века стало ясно, что теория Бора должна быть заменена другой теорией атома, в связи с чем и появилась квантовая механика.
§ 23.8. Электронные оболочки сложных атомов
Квантовые числа, описывающие состояние электрона в атоме водорода, используют для приближенной характеристики состояния отдельных электронов сложных атомов. Однако при этом следует учитывать по крайней мере два существенных отличия сложных атомов от атома водорода: 1) в сложных атомах энергия электронов из-за их взаимодействия зависит не только от п, но и от /; 2) распределение электронов по энергетическим уровням обусловлено принципом Паули, согласно которому в атоме не может быть двух (и более) электронов с четырьмя одинаковыми квантовыми числами.
При образовании электронной конфигурации, соответствующей невозбужденному состоянию атома, каждый электрон стремится иметь наименьшую энергию. Если бы не принцип Паули, то все электроны расположились бы на самом нижнем энергетическом уровне. В действительности электроны последовательно заполняют состояния, которые указаны для атома водорода в табл. 30 (за некоторыми исключениями).
Дата добавления: 2015-06-22; просмотров: 844;
