А. Метод частных дифференциалов
Частными производными функции нескольких переменных (в нашем случае 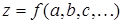 ) по одной из них называют выражения;
) по одной из них называют выражения;
а) 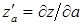 при
при 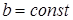 ,
, 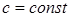 и т.д.;
и т.д.;
б) 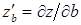 при
при 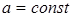 ,
, 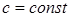 и т.д.;
и т.д.;
в) 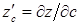 при
при 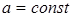 ,
, 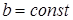 и т.д.
и т.д.
Частную производную находят по правилам дифференцирования функций одной переменной, причем остальные переменные, кроме той, по которой берут частную производную, рассматриваются как постоянные. В случае а) роль переменной играет "а", а роль постоянных - "в","с" и т.д.
Частный дифференциал определяют равенством:
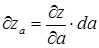 и т.д.
и т.д.
Итак, частные дифференциалы функции 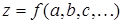 имеют вид:
имеют вид:
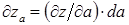 при
при 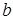 ,
, 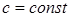
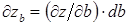 при
при 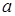 ,
, 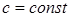
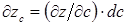 при
при 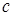 ,
, 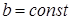
В соответствии с этим за абсолютные погрешности принимают приращения 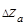 ,
, 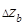 ,
, 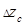 ,...
,...
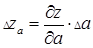 ,
, 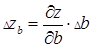 ,
, 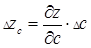 , (18)
, (18)
где 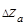 - абсолютная погрешность косвенно определяемой величина, обусловленная погрешностью
- абсолютная погрешность косвенно определяемой величина, обусловленная погрешностью 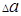 только величины "а",
только величины "а", 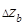 - абсолютная погрешность косвенно определяемой величины, обусловленная погрешностью
- абсолютная погрешность косвенно определяемой величины, обусловленная погрешностью 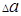 только величины "в" и т.д.
только величины "в" и т.д.
Таким образом, полная абсолютная погрешность результата косвенных измерений должна быть рассчитана по формуле:
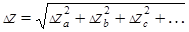 . (19)
. (19)
Дата добавления: 2015-06-22; просмотров: 1529;
