Структура механизмов. Основные определения. Образование механизмов по Ассуру.

· Механизмом называется искусственно созданная система тел, предназна­ченная для преобразования движения одного или нескольких тел в требуемые движения других тел.

Одно или несколько жестко соединенных твердых тел, входящих в состав механизма, называется звеном. Звено, принимаемое за неподвижное, называется стойкой. Звенья механизма, положения и законы движения которых задаются, назы­ваются ведущими, а звенья механизма, положения и законы движения которых одно­значно зависят от положений и законов движения ведущих звеньев, называются ведо­мыми.

Кинематической парой называется соединение двух соприкасающихся звеньев, допускающее их относительное движение. Поверхности, линии, точки звена, по которым оно может соприкасаться с другим звеном, образуя кинемати­ческую пару, называются элементами кинематической пары.

Наибольшее использование получили две классификации кинематических пар: по Артоболевскому И.И. и по Рело Ф.

По Рело Ф. кинематическая пара называется высшей, если её элементами являются линии или точки; у низших кинематических пар элементами являются плоскости или поверхности.

По Артоболевскому И.И. класс кинематической пары определяется числом условий связи, налагаемых этой парой на относительное движение её звеньев. В этой классификации выделено пять классов кинематических пар. плоские кинематические пары, звенья которых совершают движения в одной или параллельных плоскостях, могут иметь в этой классификации лишь IV или V класс. При этом пары IV класса являются высшими, а пары V класса – низшие по Рело Ф.

· Кинематической цепью называется связанная система звеньев, образую­щих между собою кинематические пары. Кинематические цепи подразделяются на простые и сложные, замкнутые и незамкнутые, плоские и пространственные.

Простой кинематической цепью называется цепь, у которой каждое звено входит не более чем в две кинематические пары.

Сложной кинематической цепью называется цепь, у которой имеется хотя бы одно звено, входящее более чем в две кинематические пары.

Замкнутой кинематической цепью называется цепь, каждое звено которой входит по крайней мере в две кинематические пары.

Незамкнутой кинематической цепью называется цепь, у которой есть звенья, входящие только в одну кинематическую пару. Плоской называется кинематическая цепь, все звенья которой совершают движения в одной или параллельных плоскостях. У пространственных цепей звенья совершают пространственные перемещения.

• Степенью подвижности 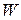кинематической цепи называется число степеней её свободы, относительно неподвижного звена (стойки) этой цепи. Для плоских кинематических цепей, которые и будем рассматривать ниже, 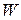определяется по формуле Чебышева П.Л.

,

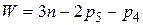где n – число подвижных звеньев цепи;

р₅ – число кинематических пар V класса, образованных всеми звеньями

цепи;

Р₄ – число кинематических пар IV класса, образованных всеми

звеньями цепи.

• Механизмом называется кинематическая цепь, в которой при заданных положениях и законах движения одного или нескольких ведущих звеньев, положения и законы движения остальных (ведомых) звеньев являются единственно определенными. Каждая замкнутая кинематическая цепь, имеющая стойку и степень подвижности W, равную числу входных звеньев, является механизмом.

• Кинематическая схема механизма – это графическое его изображение с условным представлением звеньев и кинематических пар, выполненное в масштабе, и учитывающее характер относительного движения звеньев.

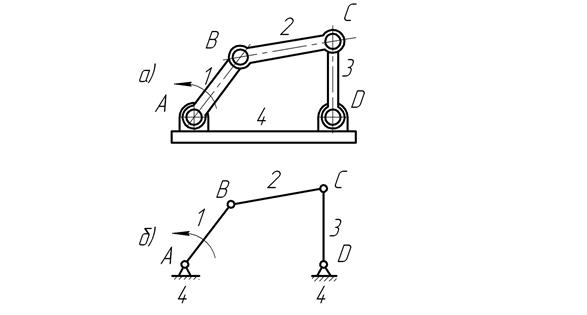
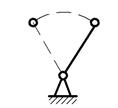
Рис. 34. Плоский шарнирный четырехзвенный механизм: а) полуконструк­тивная схема, б) кинематическая схема.

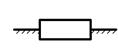
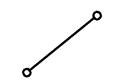
На кинематических схемах механизмов звенья, как правило, изображаются прямоугольниками и отрезками прямых и нумеруются арабскими цифрами.

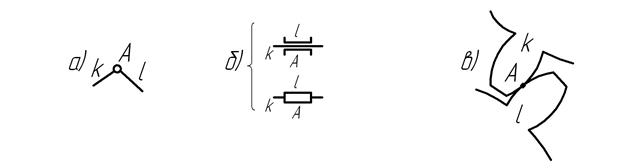
Рис. 35. Схематическое изо­бражение кинематических пар в плоских механизмах - а) шарнир-вращательная пара V класса (низшая), б) посту­пательная пара V класса (низшая), в)зацепление зубчатых профилей -кинематическая пара IV класса (высшая).

Кинематические пары в механизмах обозначаются большими буквами латинского алфавита и схематически изображаются так, как это сделано на рис.34,35. Пары IV класса очерчиваются кривыми, которыми они являются в натуре. Стойку (неподвижное звено) принято выделять штриховкой (рис. 36).

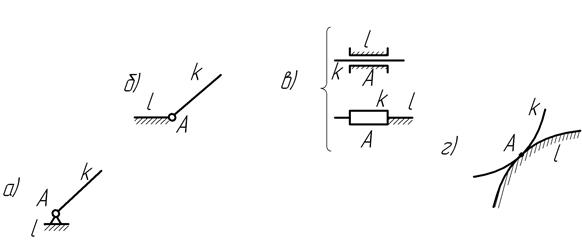
Рис.36 . Схематическое изо­бражение неподвижных эле­ментов кинематических пар: а) и б) — вращательная ки­нематическая пара, в) посту­пательная пара, г) высшая пара.

• Структурная группа – это простейшая кинематическая цепь, которая, будучи присоединена всеми своими свободными концами к стойке, имеет 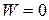и которая не может быть разбита на более простые цепи, имеющие .

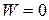Структурные группы подразделяются на классы и внутри класса на порядки. Далее будем рассматривать простейшие группы II класса и 2-го порядка, состоящие из двух звеньев и трёх кинематических пар. Такие группы подразделяются также по видам в зависимости от числа и местоположения поступательных кинематических пар (рис. 37а,б).

Рис. 37. Группы Ассура второго класса различных видов: ( а) первого, (б) второго, и механизмы I класса (в,г).

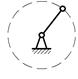
• Механизм I класса – это соединение входного звена со стойкой. Возможны два варианта таких соединений, представленные на рис. 37в,г. На изображениях механизмов I класса входное звено представляется со стойкой.

• Понятия механизм I класса и структурной группы ввёл Ассур Л.В., который также предложил названный впоследствие его именем принцип образования механизмов. Согласно ему, любой механизм образуется последовательным присоединением к одному или нескольким механизмам I класса и стойке структурных групп. При этом первая входящая в состав механизма структурная группа одним или несколькими своими свободными концами присоединяется к механизмам I класса, а оставшимися свободными концами – к стойке. Каждая последующая структурная группа одним или несколькими свободными концами присоединяется к звеньям образованной кинематической цепи; некоторыми своими свободными концами она может присоединяться к другим, не вошедшим в состав образованной цепи, механизмам I класса; оставшимися свободными концами эта структурная группа присоединяется к стойке.

• Класс механизма определяется наивысшим классом структурной группы, вошедшей в его состав. Для каждого класса механизмов разработаны свои методы их кинематического и динамического исследования. Поэтому структурное исследование механизма, сводящемся к выделению в нём структурных групп, их классификации и определению класса механизма, должно предшествовать его кинематическому и динамическому исследованию.

• Формула строения механизма – это условная запись, отражающая порядок вхождения в состав механизма всех составляющих его структуры (механизмов I класса и структурных групп). Эта формула является важнейшим результатом структурного исследования механизма, т.к. она показывает класс механизма, а значит соответствующий этому классу метод последующего кинематического и динамического исследования этого механизма. Кроме того, эта формула определяет последовательность кинематического и динамического исследования всех элементов структуры механизма. Так, кинематическое исследование проводится в порядке следования этих элементов в формуле строения механизма, динамическое исследование в обратном порядке.

Ниже представленный пример структурного исследования механизма иллюстрирует условные обозначения, используемые при записи формулы строения механизма.

• Для проведения структурного исследования задаётся схема механизма, изображённая не в масштабе, с указанием с помощью стрелок входных звеньев. Само исследование проводится в следующей последовательности:

1. Подсчитывается число n подвижных звеньев механизма, число р₅ кинематических пар V-го класса и число р₄ кинематических пар IV-го класса. Определяется степень подвижности W и если найденное значение равно числу входных звеньев, делается вывод о принадлежности рассматриваемой кинематической цепи к механизмам.

2. Т. к. далее будем рассматривать лишь механизмы с одним входным звеном, то выделяется единственный механизм I класса.

3. Оставшаяся цепь разбивается на структурные группы с соблюдением общего принципа образования механизмов по Асуру Л.В. Определяется класс каждой группы.

4. Определяется класс всего механизма.

5. Записывается формула строения механизма.

Пример структурного исследования механизма.

Схема исследуемого механизма с указанием его входного звена представлена на рис.38.

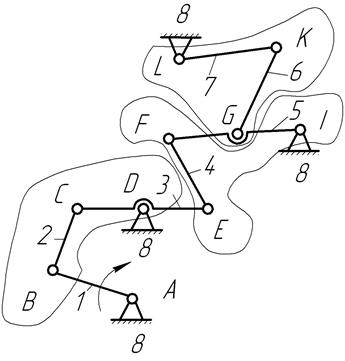
Рис. 38. Механизм автомата-пере­коса вертолета.

Решение

1. Подсчитывается степень подвижности механизма по формуле Чебышева. Для этого определяются общее число звеньев k = 8, число подвижных звеньев n = k - 1 = 7, число кинематических пар V класса р₅ =10, число кинематических пар IV класса р₄ =0 Степень подвижности

w = 3n—2р₅ — р₄ = 3*7 – 2*10 – 0 = 1.

Исследуемая кинематическая цепь является механизмом , так как при w=1 она имеет одно входное звено.

2. Выделяется механизм I класса – соединение в кинематической паре А входного звена 1 и стойки 8 – см. механизм I кл. на рис. 38.

3. Оставшуюся цепь из звеньев 2…7 разбиваем на структурные группы. Первой выделяем структурную группу II класса, состоящую из звеньев 2 и 3, которая в соответствии с принципом Ассура Л.В. одним свободным концом В присоединяется к механизму I класса, а другим свободным концом D – к стойке. Второй выделяем группу II класса из звеньев 4 и 5, которая одним свободным концом Е присоединяется к звену 3, уже включенному в схему механизма, а вторым свободным концом Q – к стойке. Аналогично третьей выделяем структурную группу II класса из звеньев 6,7, которая одним свободным концом G присоединяется к звену 5, уже включенному в схему механизма, а другим свободным концом L – к стойке.

4. Т.к. все структурные группы, входящие в состав исследуемого механизма, имеют II класс, этот механизм относится к механизмам II класса.

5. Записывается формула строения механизма.

Мех-м II = м-м I (1,8) → гр. II (2,3) → гр. II (4,5) → гр. II (6,7).

Читаются обозначения этой формулы следующим образом: исследуемый механизм имеет II класс (Мех-м II) и состоит (знак равенства) из механизма I класса, образованного звеньями 1 и 8 (м-м I (1,8)), к которому присоединяется группа звеньев II класса, образованная звеньями 2-3 – (гр. II (2,3)); к этой группе присоединяется следующая группа II класса, образованная звеньями 4 и 5 – (гр. II (4,5)); к ней присоединяется ещё одна группа II класса, образованная звеньями 6 и 7 – гр. II (6,7).

Планы положений, скоростей и ускорений точек звеньев механизмов.

Исходными данными для построения этих планов служат: кинематическая схема механизма и законы движения его входных звеньев.

По изложенной в п. 4.1 методике проводится исследование структуры заданного механизма, определяется его класс и записывается формула строения. Построение отмеченных планов проводится последовательно для всех элементов структуры механизма в порядке их исследования в формуле строения. Последовательность построения этих планов следующая:

1. Строятся планы положений механизма.

2. Строятся планы скоростей, определяются угловые скорости вращения звеньев.

3. Строятся планы ускорений, определяются угловые ускорения вращения звеньев.

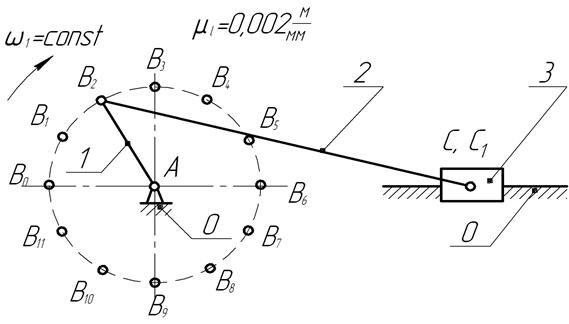
Рис.39. План положения механизма

Масштабы построения планов положений, скоростей и ускорений должны подбираться так, чтобы наиболее полно использовалось поле чертежа.

Дальнейшее решение задач построения указанных планов рассмотрим на примере кривошипно-ползунного механизма (рис. 39), для которого заданы длины звеньев 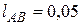м, м 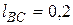и закон вращения входного звена .

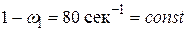В результате проведения структурного исследования по методике п. 4.1 получим формулу строения исследуемого механизма:

Мех-м II = м-м I (1,0) → гр. II (2,3).

Из этой формулы следует:

- т.к. исследуемый механизм имеет II класс, то для его кинематического исследования можно использовать излагаемые ниже методы планов;

- построение планов положений механизма и им соответствующих планов скоростей и ускорений необходимо начинать с механизмами I класса, а затем эти планы строить для звеньев группы (2,3).

4.2.1. Построение заданного плана положения механизма

Изображаем на чертеже кривошип 1 отрезком АВ = 25мм. Тогда масштаб построения планов положений механизма

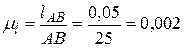м/мм.

Используя этот масштаб, находим отрезок, изображающий длину шатуна 2 –

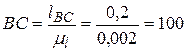мм.

Нулевым положением механизма считаем начало рабочего хода ползуна 3, когда он находится в крайнем левом положении, что будет иметь место, когда кривошип 1 расположится по горизонтали влево от точки А. Заданное положение механизма определяется углом 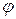₁ поворота кривошипа от нулевого его положения в направлении вращения. В рассматриваемом случае задаёмся .

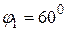Выбрав на чертеже положение точки А – центра вращения кривошипа 1, размером АВ = 25мм вычерчиваем окружность – геометрическое место возможных положений точки В. Откладываем от нулевого положения кривошипа (АВ₀ на рис. 39) угол 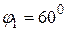, определяющий заданное положение этого звена. Строим АВ_2,, определяющий это положение.

Радиусом 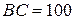мм из точки В₂ делаем засечку на прямой АС – геометрическим местом положений точки С. Получим точку С₂ с нахождением которой определяются положения шатуна 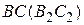и ползуна 3 в заданном положении механизма. Ползун 3 изображаем прямоугольником с произвольными сторонами; длинная сторона его параллельна заштрихованной направляющей 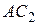. Аналогично строится план положения механизма для любого заданного положения его входного звена.

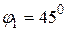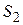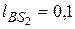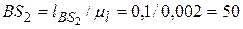На рис. 40а таким образом построим план положения механизма для угла кривошипа , отсчитываемого от горизонтали не слева (как на рис. 39), а справа от шарнира А. Там же показано положение центра масс звена 2, задаваемое либо отрезком м

( мм),

либо отношением 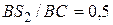, из которого 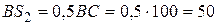мм

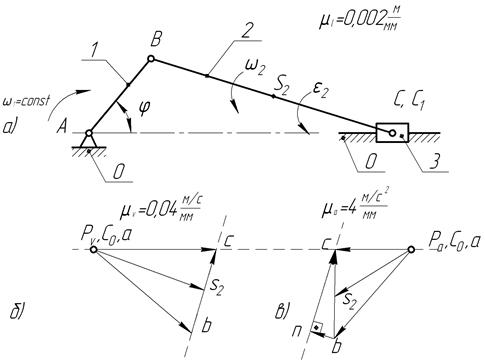
Рис.40. Кинематический анализ кривошипно-ползунного механизма компрессора: а)план положения, б) план скоростей, в) план ускорений.

4.2.2. Построение плана скоростей для заданного положения механизма

Строя сначала план скоростей механизма I класса, найдем скорость точки В кривошипа

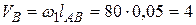мс^-1

направленную по перпендикуляру к АВ в сторону .

Приняв для изображения этой скорости на плане отрезок 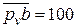мм, определяем масштаб плана скоростей

.

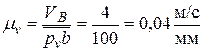Выбрав на чертеже (рис. 40б) произвольную точку р_v – полюс плана скоростей, - строим из неё вектор 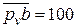мм, в масштабе 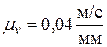представляющий величину и направление 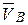. Скорость точки А кривошипа 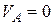, поэтому точку а – конец вектора скорости этой точки – располагаем в полюсе р_v.

Далее строим план скоростей звеньев группы II (2,3), для чего используем систему векторных уравнений:

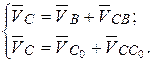
Решая эту систему, из точки b плана скоростей строим линию действия 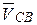- перпендикуляр к ВС – положению звена 2 на рис. 40а (эта линия действия представлена на рис. 40б пунктиром). Скорость точки С₀, принадлежащей стойке, равна нулю, потому её помещаем в полюс р_v. Скорость точки С звена 3 относительно стойки направлена по горизонтали, поэтому из точки С₀ плана скоростей проводим горизонтальную прямую (представлена пунктиром)). Две пунктирные прямые пересекаются в точке с – конец вектора абсолютной скорости точки. Изображаем вектор 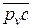этой скорости сплошной линией и находим 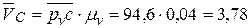м/с.

Изображаем сплошной линией вектор 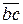и находим значения относительной скорости точек В и С звена 2 - 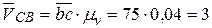м/с.

Угловая скорость звена 2 - 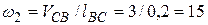с^-1. Определяя направление 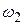, вектор 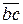из плана скоростей (см. рис. 40б) перенесём в точку С звена 2 (см. рис. 40а) и направление поворота звена 2 относительно его точки В от действия этого вектора указывает направление 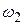. Указывают это направление круговой стрелкой на звене 2 (рис. 40а).

Построенный план скоростей механизма позволяет найти абсолютную скорость любой точки любого звена этого механизма. В частности, определяя скорость 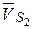центра масс звена 2, используем пропорцию

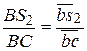, откуда 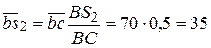мм

На отрезке 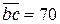мм плана скоростей откладываем 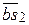, полученную точку s₂ соединяем с полюсом р_v (рис. 40б) и находим 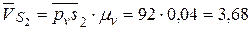мс^-2.

4.2.3. Построения плана ускорений для заданного положения механизма

Начиная с построения плана ускорений механизма I класса, найдём ускорение точки В кривошипа. Т.к. 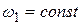, эта точка будет иметь только нормальное ускорение, определяемое как

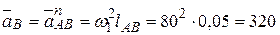м/с²

и направленное от точки В к точке А кривошипа.

Приняв для изображения этого ускорения на плане отрезок 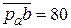мм, определяем масштаб плана ускорений

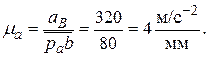
Выбрав на чертеже (рис. 40в) произвольную точку р_а – полюс плана ускорений – строим из неё вектор 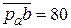мм, в масштабе 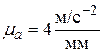представляющий величину и направление 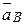. Ускорение точки А кривошипа 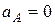, поэтому точка а – конец вектора абсолютного ускорения этой точки – располагаем в полюсе р_а.

Далее строим план ускорений звеньев группы II (2,3), для чего используем систему векторных уравнений:

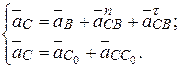
Строя правые части уравнений из полюса р_а, имеем:

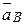· изображается уже поостренным вектором ;

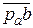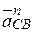· - нормальная составляющая ускорения относительного вращения точки С звена 2 относительно его точки В. По величине

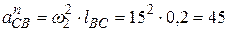мс^-2;

направлено это ускорение от точки С к точке В звена 2 и, в соответствии с первым уравнением системы, прикладывается к вектору 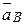. В масштабе 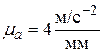ускорение 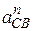представляется вектором 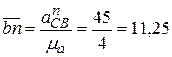мм, который и прикладываем на рис. 40в к вектору 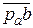, направленным от С к В;

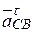· - тангенциальная составляющая ускорения относительного вращения точки С звена 2 относительно точки В. Известна лишь линия действия этой составляющей – перпендикуляр к ВС, которую и строим пунктиром из точки n плана ускорений (рис. 40в). Этим заканчивается анализ и построение слагаемых правой части первого уравнения решаемой системы векторных уравнений;

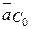· = 0 – ускорение точки С₀, принадлежащей стойке. Точку С₀ помещаем в полюс р_а;

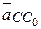· - ускорение движения точки С ползуна 3 относительно стойки. Это ускорение известно лишь по линии действия - горизонтальная прямая, которую и строим пунктиром из точки С₀ плана ускорений (рис. 40в). Пересечение двух пунктирных прямых определяет на плане ускорений (рис. 40в) положение точки с – конца вектора абсолютного ускорения С механизма.

Построенный план ускорений механизма позволяет найти абсолютное ускорение любой точки любого звена механизма. В частности, определяя ускорение 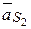центра масс звена 2, используем пропорцию:

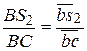, откуда 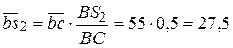мм.

На отрезке 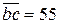мм плана ускорений откладываем 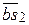, полученную точку s₂ соединяем с полюсом р_а (рис. 40в) и находим

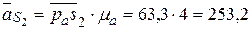мс^-2.

Из выполненных построений плана ускорений механизма также находим:

· абсолютное ускорение точки С - 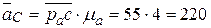мс^-2;

· тангенциальная составляющая относительного ускорения вращения точки С относительно точки В - 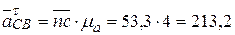мс^-2;

· угловое ускорение звена 2 - 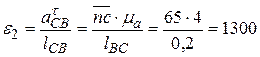с^-2. Определяя направление 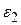вектор 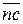плана ускорений, изображающий 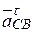переносим в точку С механизма (рис. 40а) и направление поворота звена 2 вокруг точки В от действия этого вектора указывает направление 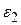(на рис. 40а направление 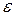показано круговой стрелкой на звене 2).