Кинематический анализ передач
Передаточным механизмом (передачей) называется механизм, преобразующий вращение одного звена, называемого ведущим, во вращение другого звена, называемого ведомым. К таким относятся зубчатые, фрикционные, цепные и другие типы передач.
Передаточным отношением такого механизма от ведущего звена k к ведомому звену l называется отношение угловой скорости ωK звена k к угловой скорости ωl звена l, т. е.
Ukl = 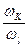 .
.
Численно передаточное отношение выражается через частоты nk , nl вращения ведущего и ведомого звеньев
Ukl = ± 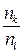 ,
,
а также через размеры этих звеньев.
Задачей кинематического анализа передач является нахождение передаточного отношения передачи через отношения размерных параметров еезвеньев.
Различают одноступенчатые передачи, такие, в которых имеются только два звена с неподвижными осями вращения, и многоступенчатые, вкоторых звеньев с неподвижными осями вращения больше двух. Ступенью передаточного механизма называется передача вращения с одной неподвижной оси вращения на другую неподвижную ось вращения. В многоступенчатых механизмах каждая из ступеней может реализовываться парой зубчатых колес, находящихся в зацеплении.
Рассмотрим методы определения передаточных отношений сложных многоступенчатых зубчатых механизмовчерез заданные числа зубьев, предварительно условившись о правилах определения знака передаточного отношения.
В одноступенчатой зубчатой передаче (рис. 44) с внешним зацеплением зубчатые колеса вращаются в противоположных направлениях, поэтому передаточное отношение такой передачи является отрицательным:
U12 = 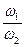 =–
=– 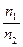 = –
= – 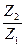 .
.
В одноступенчатой передаче с внутренним зацеплением (рис.45) зубчатые колеса вращаются в одну сторону, поэтому передаточное отношение положительно:
U12 = 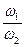 =
= 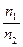 =
= 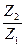 .
.
Рассмотрим многоступенчатое соединение зубчатых колес, в котором имеется k параллельных валов; на каждом из( k – 2) промежуточных валов закреплено
по два зубчатых колеса, зацепляющихся с колесами, закрепленными на предыдущем и последующем валах (рис.46 ), число его ступеней- (k-1). Такое зацепление называется последовательным. Запишем для каждой из пар зубчатых колес ступеней передаточное отношение.
U12 = 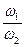 = –
= – 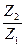 ; U23 =
; U23 = 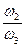 = –
= – 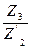 , …., UК-1,К =
, …., UК-1,К = 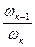 =–
=– 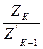 .
.
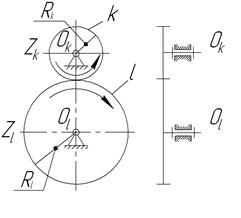
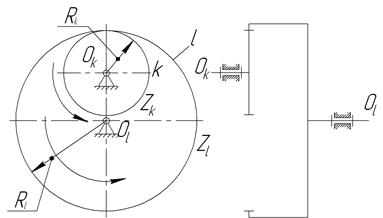
Рис.44.Трехзвенная зубчатая Рис.45. Трехзвенная зубчатая передача передача с внешним зацеплением с внутренним зацеплением колес
Перемножив почленно выражения передаточных отношений, получим
U12 U23… UК-1,К = 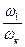 =
= 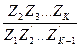 (-1)m,
(-1)m,
где m – число внешних зацеплений колес передачи.
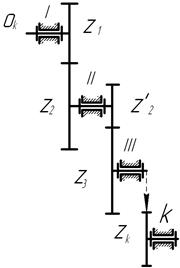
Рис.46.Последовательное рядовое зацепление колес
Передаточное отношение всей передачи, представленной на рис. 46, определится как
U1K = 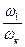 = U12 U23… UК-1,К .
= U12 U23… UК-1,К .
Передаточное отношение последовательного зацепления, как это следует изформулы, равно произведению передаточных отношений всех его ступеней.
Если при подсчете U1K получится отрицательным, то это означает, что ведомое колесо k вращается противоположно ведущему колесу 1.
Если на каждом из валов закреплено по одному колесу, входящему одновременно в зацепление с колесами на предыдущем и последующем валах, то такое зацепление называется рядовым или паразитным рядом, а все промежуточные колеса называются паразитными (рис. 47). Полное передаточное отношение паразитного ряда можно получить, приняв Z2= Z'2, Z3= Z'3, Z4 =Z4' и т. д.;
U1K = 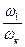 =
= 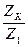 (—1) т.
(—1) т.
Последнее выражение показывает, что паразитные колеса на величину передаточного отношения не влияют, однако их включение может изменить знак передаточного отношения. Если число паразитных колес четное, то знак передаточного отношения такой же, как если бы колеса Z1 и Z2 зацеплялись
непосредственно. Нечетное число паразитных колес меняет знак передаточного числа на противоположный. Паразитные зубчатые колеса применяют в тех случаях, когда расстояние между ведущим и ведомым валами велико и непосредственно зацепляющиеся колеса увеличивают габаритные размеры механизма, или же в тех случаях, когда нужно соответственно изменить направление вращения ведомого вала.
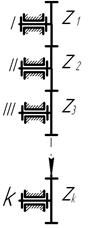
| Рис.47.Паразитный ряд |
4.6. Передача цилиндрическими зубчатыми колесами.
Если на дисках имеются зубья определенного профиля, расположенные на равном расстоянии один от другого, то передача будет называться зубчатой (рис. 48). При вращении ведущего зубчатого колеса его зубья взаимодействуют с находящимися в контакте (зацеплении) зубьями ведомого колеса, в результате чего оно также начинает вращаться.
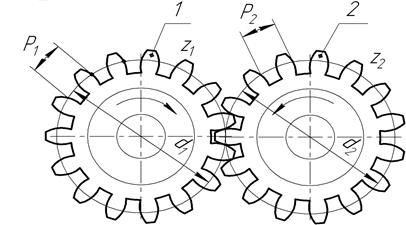
Рис.48. Зубчатая цилиндрическая передача с внешним зацеплением
Наиболее распространены передачи с эвольвентным профилем зуба. Такой профиль позволяет зубьям при вращении колес обкатываться друг по другу, отчего зубчатая передача работает плавно, с небольшими потерями энергии на трение. При вращении зубчатых колес можно представить себе две касающиеся окружности 1 и 2 (см. рис. 48), которые катятся одна по другой без скольжения. Это воображаемые окружности dw1 и dw2, — диаметры которых называют начальными окружностями. Зацепление зубчатых колес в передаче требует соблюдения основного условия : зуб одного колеса должен точно входить в соответствующую ему при зацеплении впадину другого колеса. Ширину зуба и впадины, а также другие элементы зацепления рассчитывают по так называемым делительным окружностям. Это такие окружности диаметров d1, d2, на которых размеры основных элементов зубчатого колеса равны теоретическим размерам элементов зуборезного инструмента, поэтому делительные окружности используются при расчетах для настройки зуборезного станка. При изготовлении зубчатых колес часто делительная окружность совпадает с начальной (d1=dw1, d2= dw2) . Таким образом, можно сказать, что зубчатое зацепление возможно лишь при равенстве окружных шагов р, измеренных по дугам начальных окружностей (рис. 49). Шаг — это длина отрезка дуги начальной окружности, равная длине всей начальной окружности, разделенной на число зубьев Z. На одном колесе эта зависимость выразится так:
p = 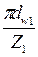 ,
,
на другом
p = 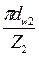 .
.
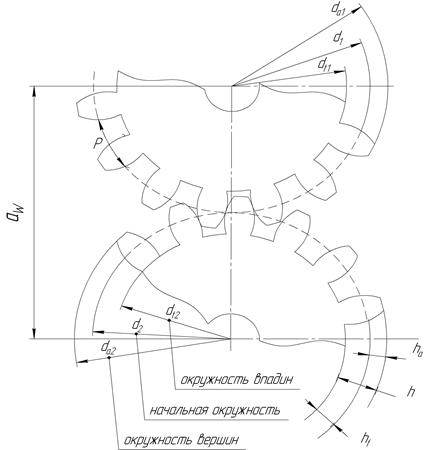
Рис. 49. Элементы зубчатого зацепления
Отсюда
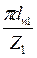 =
= 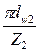 ,
,
или передаточное отношение
U12 = 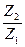 =
= 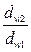 .
.
4.7. Геометрические элементы зубчатого зацепления.
Шаг зубчатой передачи по делительной окружности
 p =
p = 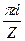 ,
,
где d –диаметр делительной окружности зубчатого колеса.
Отсюда:
для первого колеса d1 = 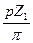 ;
;
для второго d2 = 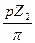 .
.
В обоих выражениях есть одна и та же величина 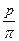 . Поскольку эта величина не может быть подсчитана точно из-за наличия иррационального числа π, более удобно взамен ее ввести величину, называемую модулем зубчатого колеса:
. Поскольку эта величина не может быть подсчитана точно из-за наличия иррационального числа π, более удобно взамен ее ввести величину, называемую модулем зубчатого колеса:
m= 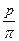
Модуль является основной геометрической характеристикой зубчатого колеса. Величина модуля стандартизована, это облегчает изготовление и подбор зубчатых колес.
Расстояние от делительной окружности до вершины зуба называется головкой зуба ha (см. рис.49), а от делительной окружности до основания зуба — ножкой зуба hf. При изготовлении колес стандартным зуборезным инструментом высота головки зуба получается равной т, а высота ножки 1,25 т. Таким образом, полная высота зуба h=2,25 т. Для цилиндрического зубчатого колеса, у которого d=dW ,можно легко определить основные размеры:
диаметр делительной окружности d=mz,
диаметр окружности вершин da=d+2 ha=m(z+2),
диаметр окружности впадин df=d—2 hf=m(z—2,5).
Расстояние между центрами колес (межосевое расстояние)
aW = 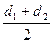 =
= 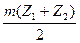 .
.
Методы изготовления зубчатых колес тесно связаны с теорией зацепления. Зубчатые колеса с эвольвентным профилем изготовляют главным образом методом копирования и методом обкатки. При методе копирования профиль режущего инструмента должен соответствовать профилю впадины нарезаемого колеса. При методе обкатки (огибания) зуборезный инструмент и нарезаемое колесо как будто находятся в действительном зацеплении, то есть начальная окружность ( начальная прямая) инструмента и начальная окружность колеса касаются друг друга и обкатывают одна другую без скольжения. Этим объясняется название метода.
Дата добавления: 2015-06-17; просмотров: 1667;
