Швидкості молекул. Правило статистичного усереднення

Хаотичний тепловий рух молекул характеризується трьома швидкостями: найбільш ймовірною, середньою арифметичною і середньою квадратичною.

Найбільш ймовірну швидкістьV_н.й мають більшість молекул. Це значення аргументу, яке відповідає максимуму функції (6.19). Знайдемо її, дослідивши функцію Максвелла (6.19) на екстремум.

. .

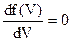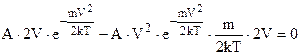. Після спрощень маємо 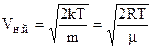. (6.22)

Тут враховано що .

Знайдемо середню арифметичну швидкість V_{ср. ар.} з таких міркувань: швидкість V₁ мають ∆N(V₁) молекул;

швидкість V₂ мають ∆N(V₂) молекул;

------------------------------------------------

швидкість V_k мають ∆N(V_k) молекул.

Середня арифметична швидкість

,

або з врахуванням (6.16) одержуємо

. (6.23)

Одержане співвідношення називається правилом статистичного усереднення. Так знаходяться середні значення фізичних величин при відомій функції розподілу по цій фізичній величині. Наприклад, середня енергія може бути знайдена за виразом

.

Розрахуємо середню арифметичну швидкість, скориставшись (6.23) і (6.21).

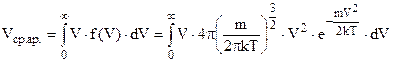. Виконаємо заміну аргументу інтегрування таку ж, як і в розділі 6.6.

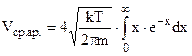. Інтегрування по частинам дає

. Одержуємо

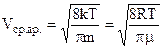. (6.24)

Знайдемо середню квадратичну швидкість V_ср.кв – це квадратний корінь із середнього значення квадратів швидкостей

.

Аналогічно попередньому, інтегрування по частинам, дає

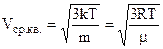. (6.25)

Можна середню квадратичну швидкість знайти простіше, знаючи середню енергію поступального руху молекул (6.13) і означення (6.11) середньої квадратичної швидкості.

.

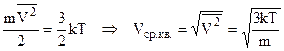Видно (6.22), (6.24) і (6.25), що всі характерні швидкості відрізняються числовими коефіцієнтами і із збільшенням температури зростають пропорційно .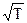

6.8 Експериментальна перевірка Максвеллівського розподілу молекул по швидкостям (дослід Штерна)

Перша експериментальна перевірка Максвеллівського розподілу молекул по швидкостям була здійснена німецьким фізиком О.Штерном (1888-1969) у 1920 р. Схема досліду показана на рис 6.8. Вздовж осі двох 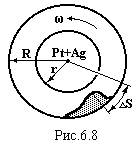коаксіальних циліндрів була натягнута платинова нитка, покрита сріблом. Внутрішній циліндр мав вузьку щілину. Вся система була поміщена у вакуум. При нагріванні нитка срібло випаровувалось. Щілиною формувався пучок атомів срібла, які осідали на внутрішній поверхні більшого циліндра напроти щілини. Коли циліндри приводились в обертання (~2700 об/хв), срібна пляма зміщувалась і розмивалась так як за час прольоту атомів між циліндрами вони встигали повернутися на певний кут. Зміщення 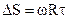. Тоді швидкість атомів 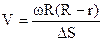. По зміщенню максимуму плями знаходили найбільш ймовірна швидкість (~600 м/с), яка добре узгоджувалась з розрахованим по (6.22) значенням. Вимірювання товщини плівки срібла з різним зміщеннями дали можливість впевнитись у справедливості формули (6.19), так як молекули з різними швидкостями зазнавали різного зміщення: повільні молекули – більшого, швидкі – меншого.