Выбор основной системы
Основная система метода перемещений должна быть кинематически определимой. Значит, для ее получения в заданную систему следует ввести столько дополнительных связей, чтобы концы всех стержней были закреплены и исключены их перемещения. Поэтому общее число вводимых связей будет равно числу неизвестных метода перемещений.
Однако число вводимых связей (а значит и число неизвестных метода перемещений) может быть весьма большим. Например, рама на рис. 10.2 а состоит из пяти стержней. По результатам проведенного выше анализа, степень ее кинематической неопределимости (или число неизвестных метода перемещений) будет 5·3=15.
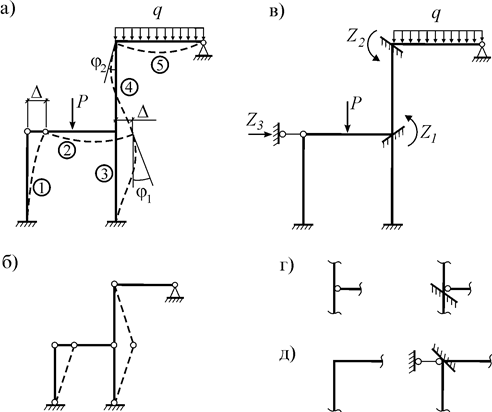
Рис. 10.2
Это число можно уменьшить, если принять следующие гипотезы:
1) поперечные и продольные деформации стержней малы;
2) длина хорды, соединяющей концы изогнутого стержня, равна первоначальной длине стержня;
3) в упругом рамном узле углы между стержнями сохраняются.
Действительно, в этом случае в данной раме достаточно будет знать только три перемещения – поступательное перемещение 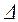 и два угловых перемещения
и два угловых перемещения 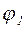 и
и 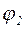 (рис. 10.2 а). Таким образом, число неизвестных уменьшилось намного – с пятнадцати до трех.
(рис. 10.2 а). Таким образом, число неизвестных уменьшилось намного – с пятнадцати до трех.
Из третьей гипотезы следует, что число неизвестных угловых перемещений будет определяться по формуле
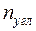 = числу упругих рамных узлов.
= числу упругих рамных узлов.
Для определения числа неизвестных поступательных перемещений (в дальнейшем их будем называть линейными перемещениями) во все узлы рамы, включая и опоры, нужно ввести шарниры (рис. 10.2 б). Тогда число линейных перемещений будет легко определяться по известной формуле кинематического анализа для фермы
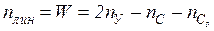 .
.
В рассматриваемой раме имеем 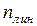 =2× 6 – 5 – 6 =1.
=2× 6 – 5 – 6 =1.
Общее число всех неизвестных перемещений определяется по формуле
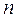 =
= 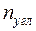 +
+ 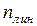
и называется степенью кинематической неопределимости. Сами неизвестные перемещения обозначаются однотипно: 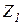 ,
, 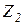 ,
, 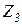 , ...,
, ..., 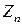 .
.
После определения числа неизвестных в ЗС следует вводить столько же связей для исключения перемещений концов ее стержней. Например, в рассмотренную раму введем две заделки и одну опорную связь. Полученная схема (рис. 10.2 в) будет основной системой (ОС) метода перемещений.
Таким образом, для получения ОС метода перемещений необходимо:
– в упругие рамные узлы заданной системы ввести 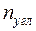 заделок;
заделок;
– в направлении поступательных перемещений узлов заданной системы ввести 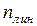 опорных связей (они вводятся так, чтобы система с введенными шарнирами стала геометрически неизменяемой).
опорных связей (они вводятся так, чтобы система с введенными шарнирами стала геометрически неизменяемой).
Введенные связи, хотя внешне и похожи на обычные опорные связи, от них принципиально отличаются, потому что: 1) введенная заделка исключает лишь угловое перемещение узла, оставляя возможность линейного смещения; 2) введенная опорная связь исключает только линейное перемещение узла, оставляя возможность поворота (рис. 10.2 г, д).
При соблюдении этих требований ОС метода перемещений будет единственной.
Пусть необходимо выбрать ОС метода перемещений для рамы (рис. 10.3 а). Она имеет четыре жестких узла. Значит, число угловых неизвестных 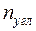 =4. Для определения числа линейных неизвестных во все узлы и опоры рамы введем шарниры (рис. 10.3 б). Тогда имеем:
=4. Для определения числа линейных неизвестных во все узлы и опоры рамы введем шарниры (рис. 10.3 б). Тогда имеем: 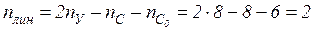 . Поэтому общее число неизвестных будет
. Поэтому общее число неизвестных будет 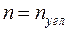 +
+ 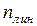 =4+2=6. Вводя в жесткие узлы ЗС четыре заделки и две опоры, исключающие линейные перемещения узлов рамы (последние вводятся так, чтобы механизм на рис. 10.3 б стал геометрически неизменяемым), получаем требуемую ОС (рис. 10.3 в).
=4+2=6. Вводя в жесткие узлы ЗС четыре заделки и две опоры, исключающие линейные перемещения узлов рамы (последние вводятся так, чтобы механизм на рис. 10.3 б стал геометрически неизменяемым), получаем требуемую ОС (рис. 10.3 в).
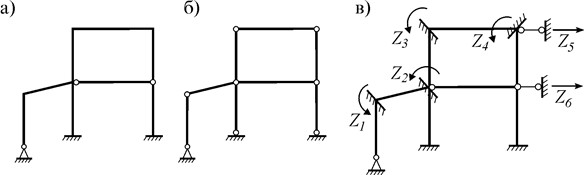
Рис. 10.3
Дата добавления: 2015-06-17; просмотров: 863;
