Число степеней свободы стержневой системы
Рассматривая расчетную схему сооружения как систему дисков, объединенных связями, получаем ее дисковый аналог. Для одной и той же системы часто можно получить несколько дисковых аналогов.
Число степеней свободы плоской стержневой системы определяется по формуле, называемой основной формулой кинематического анализа:
W = 3nД – 2nШ – nC –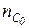 
– 3nП .
Здесь nД – число дисков в дисковом аналоге; nШ – число простых шарниров; nС – число стержней; 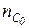– число опорных связей; nП – число припаек.
При расчете фермы можно использовать формулу
W = 2nУ – nC – ,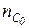
где nУ – число узлов фермы (узлом считается любой шарнир, связывающий стержни фермы).
После расчета по этим формулам возможны три случая:
1) W>0 – такая система геометрически изменяема и является механизмом;
2) W=0 –в системе имеется достаточное число связей; если они введены правильно, то система неизменяема и статически определима;
3) W<0 – в системе есть избыточные связи. Если эти связи введены правильно, то система неизменяема и статически определима.
Отсюда следует, что расчетная схема сооружения должна удовлетворять необходимому условию геометрической неизменяемости
W£ 0.
В качестве примера рассмотрим три расчетные схемы (рис. 2.6 а, в, д) и их дисковые аналоги (рис. 2.6 б, г, е, ж).
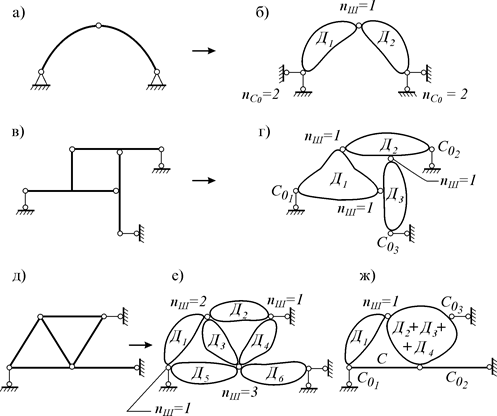
Рис. 2.6
Вычислим число степеней свободы этих систем:
1) арка (рис. 2.6 а): nД=2, nШ=1, nC=0,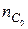 
=4, nП=0;
W=3×2 – 2×1 – 0 – 4 –3×0 =0;
2) рама (рис. 2.6 в): nД=3, nШ=3, nC=0, 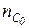=3, nП=0;
W=3×3 – 2×3 – 0 – 3 –3×0 =0.
3) ферма (рис. 2.6 д):
– по дисковому аналогу (рис. 2.6 е): nД=6, nШ=7, nC=0, 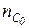=4, nП=0;
W = 3×6 – 2×7 – 0 – 4 –3×0 = 0;
– по дисковому аналогу (рис. 2.6 ж): nД=2, nШ=1, nC=1, 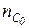=3, nП=0;
W = 3×2 – 2×1 – 1 – 3 –3×0 = 0;
– по формуле для фермы (рис. 2.6 д): nУ=4, nС=5, 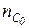=3;
W = 2×4 – 5 – 3 = 0.
Дата добавления: 2015-06-17; просмотров: 910;