Тема №7. Относительный лопаточный КПД ступени
После того, как мы научились на прошлой лекции определять работу, совершаемую ступенью турбины, необходимо поговорить о эффективности получения этой работы, т.е. о КПД ступени.
Вообще ступень турбины характеризуется двумя видами КПД:
1. Относительным лопаточным КПД;
2. Относительным внутренним КПД.
Рассмотрим первый из них.
Относительный лопаточный КПД – это отношение мощности, вырабатываемой ступенью к располагаемой энергии этой ступени:
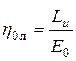 .
.
Однако для отдельной ступени понятие располагаемой энергии несколько условно.
Мы уже говорили, что кинетическая энергия 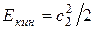 , с которой рабочее тело покидает ступень, может рассматриваться как потеря, вызванная несовершенством работы данной ступени.
, с которой рабочее тело покидает ступень, может рассматриваться как потеря, вызванная несовершенством работы данной ступени.
Тогда можно принять, что
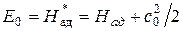 .
.
Если из всей энергии 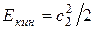 в данной ступени можно использовать только часть, то
в данной ступени можно использовать только часть, то
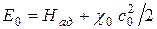 ,
,
где 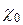 -- коэффициент использования энергии с входной скоростью в данной ступени.
-- коэффициент использования энергии с входной скоростью в данной ступени.
В многоступенчатых турбинах кинетическая энергия 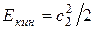 рабочего тела на выходе из ступени может быть полностью или частично использована в последующих ступенях. В этом случае нет оснований включать
рабочего тела на выходе из ступени может быть полностью или частично использована в последующих ступенях. В этом случае нет оснований включать 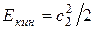 в величину располагаемой энергии данной ступени. Поэтому:
в величину располагаемой энергии данной ступени. Поэтому:
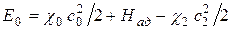 ,
,
где 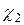 -- коэффициент использования энергии с выходной скоростью в последующей ступени.
-- коэффициент использования энергии с выходной скоростью в последующей ступени.
Естественно, что оба коэффициента и 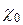 , и
, и 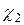 изменяются от 0 до 1.
изменяются от 0 до 1.
Хорошо видно, что при 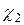 =1, т.е. при возможности использовать энергию с выходной скоростью в последующей ступени располагаемая энергия ступени увеличивается, а КПД соответственно возрастает.
=1, т.е. при возможности использовать энергию с выходной скоростью в последующей ступени располагаемая энергия ступени увеличивается, а КПД соответственно возрастает.
Это факт является одним из преимуществ многоступенчатых турбин.
Преобразуем формулу для вычисления относительного лопаточного КПД ступени:
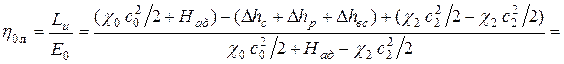
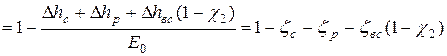 ,
,
где 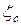 ,
, 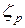 и
и 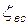 -- относительные потери в соплах, рабочем колесе и с выходной скоростью.
-- относительные потери в соплах, рабочем колесе и с выходной скоростью.
При рассмотрении расширения рабочего тела в соплах и рабочих каналах мы уже вводили понятие относительных потерь 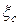 и
и 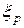 , которые характеризовали совершенство этих отдельно взятых устройств (в отрыве от ступени).
, которые характеризовали совершенство этих отдельно взятых устройств (в отрыве от ступени).
Естественно, что 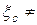
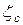 , а
, а 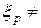
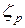 , т.к.
, т.к. 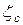 и
и 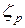 характеризуют уже уровень потерь в СА и РК в составе все ступени.
характеризуют уже уровень потерь в СА и РК в составе все ступени.
Вспомним, что при условии 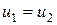 :
:
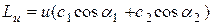 ,
,
а из рассмотрения h-s – диаграммы (рис. 5.6) можно вывести, что
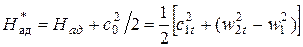 .
.
Тогда выражение для вычисление относительного лопаточного КПД можно записать:
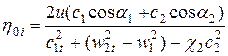
Таким образом, относительный лопаточный КПД находится в сложной зависимости от кинематических характеристик ступени.
Фактически относительный лопаточный КПД будет характеризовать степень аэродинамического совершенства ступени.
Характеристический коэффициент ступени
С понятием фиктивной скорости, которое мы ввели ранее, связан один из важнейших безразмерных параметров ступени – характеристический коэффициент:
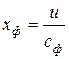 .
.
Вспомним, что еще в 50-х годах XIX века Лавалем было установлено, что для эффективного использования кинетической энергии пара окружная скорость лопаток турбины на периферии должна быть не менее половины скорости обдувающей струи.
Это привело к тому, что частоты вращения активных турбин Лаваля достигали 30 000 об/мин.
Вообще характеристический коэффициент несет в себе глубочайший смысл и означает, что при имеющейся геометрии ступени, которая определяется вопросами технологии изготовления и прочности, со ступени можно снять вполне определенный теплоперепад при условии максимальной эффективности.
Рассмотрим пример.
Теплоперепад на газовую турбину в зависимости от начальных параметров составляет 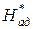 =500…600 кДж/кг.
=500…600 кДж/кг.
Предположим, что весь этот теплоперепад срабатывается в одной ступени.
Фиктивная скорость при этом составит:
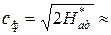 1000…1100 м/с.
1000…1100 м/с.
Окружная скорость (используя соотношение, полученное Лавалем):
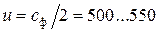 м/с.
м/с.
При среднем диаметре ступени Dср=1 м частота вращения ротора составит тогда:
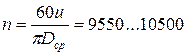 об/мин.
об/мин.
Таким образом, срабатывание значительных теплоперепадов в одной ступени возможно только при высоких частотах вращения ротора.
Парсонс же, как мы знаем, решил задачу эффективного преобразования энергии в турбинной ступени иначе – он разделил теплоперепад турбины между несколькими ступенями, что позволило снизить окружные скорости (частоту вращения) до умеренных величин.
Вернемся непосредственно к характеристическому коэффициенту.
Оказывается, что любое отклонение от оптимального соотношения между геометрией и теплоперепадом ступени будет приводить к снижению ее эффективности (КПД). Более подробно этот вывод будет рассмотрен ниже.
Отметим также, что соотношение 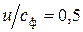 , полученное Лавалем справедливо лишь для ступеней активного типа. Существуют ступени, у которых оптимальное соотношение
, полученное Лавалем справедливо лишь для ступеней активного типа. Существуют ступени, у которых оптимальное соотношение 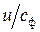 имеет другие значения, принимая при этом значения от 0,17 до 0,70. Естественно, что при этом конструкция ступени может претерпевать серьезные изменения. Более подробно об этом мы также поговорим позже.
имеет другие значения, принимая при этом значения от 0,17 до 0,70. Естественно, что при этом конструкция ступени может претерпевать серьезные изменения. Более подробно об этом мы также поговорим позже.
Характеристический коэффициент получил наибольшее распространение в паротурбостроении. В газотурбостроении наряду с ним пользуются также понятием коэффициента нагрузки:
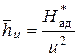 .
.
Можно показать, что для активной ступени:
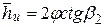 ,
,
а для реактивной
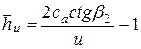 .
.
Из данных формул следует, что максимальное значение коэффициента нагрузки 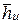 = 2 достигается при осевом выходе потока из ступени (
= 2 достигается при осевом выходе потока из ступени ( 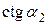 = 0) и степени реактивности r = 0. Дальнейшее увеличение
= 0) и степени реактивности r = 0. Дальнейшее увеличение 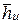 может быть получено лишь при r < 0, что нежелательно, так как вызывает снижение КПД ступени.
может быть получено лишь при r < 0, что нежелательно, так как вызывает снижение КПД ступени.
Поскольку в действительности коэффициенты скорости ( 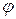 и
и 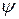 зависят от
зависят от 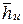 и хф и зависимость эта является достаточно сложной и неоднозначной, на практике целесообразно использовать экспериментальные данные, полученные для типовых ступеней. В качестве примера на рис. 7.1 приведены экспериментальные зависимости
и хф и зависимость эта является достаточно сложной и неоднозначной, на практике целесообразно использовать экспериментальные данные, полученные для типовых ступеней. В качестве примера на рис. 7.1 приведены экспериментальные зависимости 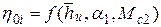 . Здесь
. Здесь 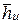 — коэффициент нагрузки в корневом диаметре ступени, где обычно имеют место максимальные значения числа Маха Мw1, и наибольшие углы поворота в каналах лопаток рабочего колеса.
— коэффициент нагрузки в корневом диаметре ступени, где обычно имеют место максимальные значения числа Маха Мw1, и наибольшие углы поворота в каналах лопаток рабочего колеса.
а. б.
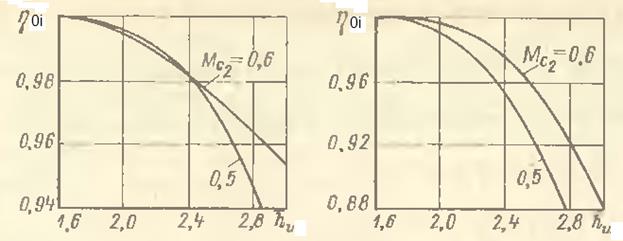
Рис. 7.1. Зависимости 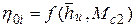 : а. – a1ср=18…25°; б. – a1ср=30…36°;
: а. – a1ср=18…25°; б. – a1ср=30…36°;
Формула Банки
Формулу для вычисления относительного лопаточного КПД можно еще несколько преобразовать после введения коэффициента 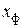 .
.
Для этого запишем скорости с1 и w2 в следующем виде:
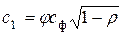 ;
;
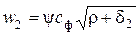 ,
,
где 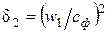 .
.
Саму формулу для вычисления 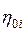 перепишем, пренебрегая
перепишем, пренебрегая 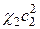 :
:
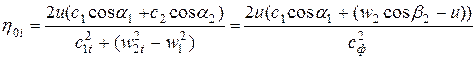 =
=
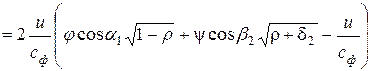 .
.
Для того, чтобы избавиться от коэффициента 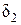 , скорость
, скорость 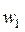 запишем в виде:
запишем в виде:
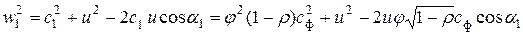
и подставим в формулу.
После некоторых преобразований получим:
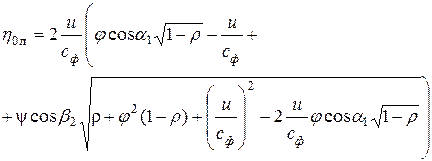 .
.
Формула для вычисления  в такой записи и получила название формула Банки.
в такой записи и получила название формула Банки.
В таком виде хорошо видно, что относительный лопаточный КПД представляет собой функцию отношения скоростей u/cф, степени реактивности r, углов потока a1 и b2, коэффициентов скоростей  и
и 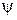 , т.е. еще раз показывает то, что относительный лопаточный КПД характеризует степень аэродинамического совершенства ступени.
, т.е. еще раз показывает то, что относительный лопаточный КПД характеризует степень аэродинамического совершенства ступени.
Относительный лопаточный КПД ступени активного типа
Вычисление КПД чисто активной ступени – это частный случай применения формулы Банки, рассмотрение которого позволяет получить ряд важных выводов, не прибегая к сложным вычислениям.
Для чисто активной ступени степень реактивности r=0. Подставляя это значение в формулу Банки, после некоторых преобразований получим:
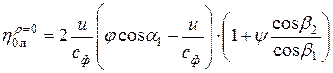
При выводе данной формулы применяются следующие соотношения:
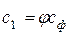 и
и 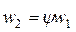 .
.
В первом приближении можно считать, что 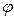 ,
, 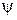 , a1 и
, a1 и 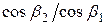 являются константами.
являются константами.
Если построить зависимость 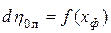 при таких условиях, то получится параболическая зависимость (см. рис. 7.2).
при таких условиях, то получится параболическая зависимость (см. рис. 7.2).
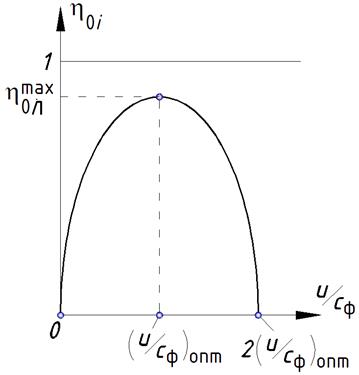
Рис. 7.2. Зависимость относительного лопаточного КПД от характеристического коэффициента ступени
Взяв производную 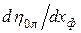 и прировняв ее к нулю, можно получить значение
и прировняв ее к нулю, можно получить значение 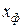 , при котором
, при котором 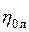 имеет экстремум (максимум):
имеет экстремум (максимум):
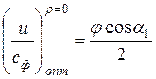 .
.
Это значение характеристического коэффициента получило название оптимального, т.е. при выполнении ступени с таким характеристическим коэффициентом относительный лопаточный КПД будет принимать максимально возможное значение.
Если в эту формулу подставить возможные значения 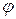 и
и 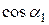 , то для активной ступени получится
, то для активной ступени получится 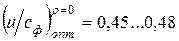 .
.
Именно к такому соотношению пришел Лаваль эмпирическим путем!
Максимальное значение КПД при этом может быть вычислено по формуле:
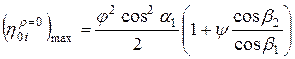 .
.
Параболическое протекание кривой КПД на рис. 7.2 определяется законами изменения отдельных потерь ступени в зависимости от отношения 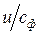 .
.
Аналогичную зависимость можно получить, если непосредственно подсчитать величины потерь в СА, РК и с выходной скоростью (рис. 7.3).
Из рассмотрения рис. 7.3, где изображены зависимости потерь от значения коэффициента 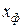 , можно сделать вывод о том, что именно значение потерь с выходной скоростью в наибольшей степени растет при отклонении отношения u/cф от оптимального значения.
, можно сделать вывод о том, что именно значение потерь с выходной скоростью в наибольшей степени растет при отклонении отношения u/cф от оптимального значения.
Этот факт хорошо виден при рассмотрении деформаций треугольников скоростей (рис. 7.4).
Если исходить из условия, что теплоперепад ступени (сф) постоянен, а также предположить, что углы a1 и b2 не изменяются, то очень легко показать изменения, происходящие с треугольниками скоростей при различных значениях коэффициента 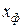 .
.
При значениях коэффициента 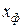 меньше оптимального ступень срабатывает теплоперепад больше оптимального, в треугольниках скоростей при этом a1 <90º.
меньше оптимального ступень срабатывает теплоперепад больше оптимального, в треугольниках скоростей при этом a1 <90º.
При значениях коэффициента 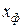 больше оптимального ступень срабатывает теплоперепад меньше оптимального, в треугольниках скоростей при этом a1 >90º.
больше оптимального ступень срабатывает теплоперепад меньше оптимального, в треугольниках скоростей при этом a1 >90º.
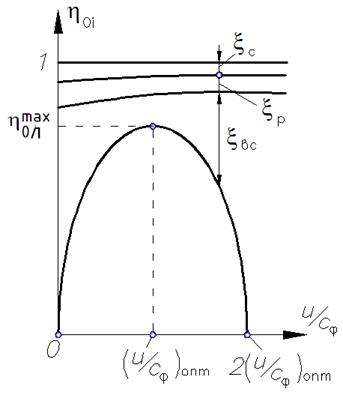
Рис. 7.3.Зависимость потерь от КПД от характеристического коэффициента ступени
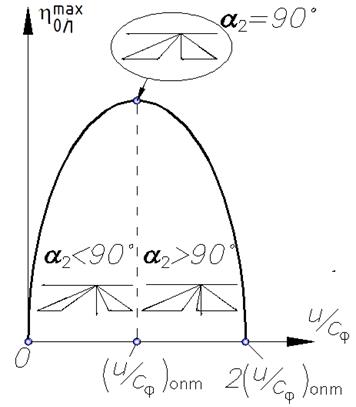
Рис. 7.4. Деформирование треугольников скоростей в зависимости от характеристического коэффициента ступени
И наконец, при оптимальном значении коэффициента 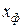 ступень срабатывает оптимальный теплоперепад, а треугольники скоростей, в которых a1 =90º, называются оптимальными треугольниками скоростей. Оптимальный относительный КПД ступени при этом максимален за счет минимальных потерь с выходной скоростью.
ступень срабатывает оптимальный теплоперепад, а треугольники скоростей, в которых a1 =90º, называются оптимальными треугольниками скоростей. Оптимальный относительный КПД ступени при этом максимален за счет минимальных потерь с выходной скоростью.
Относительный лопаточный КПД реактивной ступени
Если провести действия с уравнением Банки для реактивной ступени (r≠0), аналогичные тем, что были проделаны для ступени активной, то можно показать, что формула для вычисления оптимального отношения скоростей u/cф в общем виде
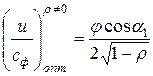 .
.
При сравнении ступеней с r=0 и r=0,5 по данной формуле видно, что при равной геометрии и частоте вращения (u, j и a1) оптимальные соотношения скоростей составят 0,5 и 0,7 соответственно.
Очень легко показать, что оптимальный теплоперепад активной ступени при таких условиях в 2 раза выше, чем в ступени реактивной.
На рис. 7.5 показано сравнение зависимостей относительного лопаточного КПД активной и реактивной ступеней от отношения скоростей u/cф.
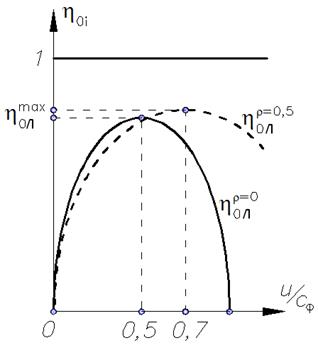
Рис. 7.5. Сравнение активной и реактивной ступеней
Проведен некоторый анализ:
1. С ростом степени реактивности ступени растет оптимальное отношение скоростей u/cф, растет максимально достижимый относительный лопаточный КПД, но снижается значение оптимального теплоперепада.
2. С ростом степени реактивности зависимость 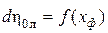 становится более пологой, что делает такие ступени больше приспособленными для работы на переменных режимах (КПД снижается менее интенсивно).
становится более пологой, что делает такие ступени больше приспособленными для работы на переменных режимах (КПД снижается менее интенсивно).
Ступени скорости
Теплоперепад, срабатываемый в ступени турбины, зависит от окружной скорости u и оптимального отношения скоростей u/cф.
Допустимые значения окружной скорости u ограничены условиями прочности.
Если uср =140…210 м/с, то значения теплоперепадов на ступень находятся на уровне 45…100 кДж/кг.
В некоторых случаях требуется сработать значительно больший теплоперепад при умеренной скорости u и относительно высоком КПД.
Для увеличения теплоперепада на ступень необходимо снижение характеристического коэффициента, что, как мы уже знаем, ведет к росту потерь с выходной скоростью и, следовательно, снижается КПД.
Оригинально решение было предложено Лавалем и Кертисом – они предложили использовать повышенную скорость с2 на втором венце рабочих лопаток, для чего перед ними необходимо поставить ряд направляющих лопаток, которые повернут струю газа и подадут его на рабочие лопатки под необходимым углом. Если по выходе из второй ступени скорость газа окажется все еще значительной, можно поставить третью ступень и так далее для снижения выходной скорости до приемлемой величины. Таким образом можно свести выходную потерю к минимуму даже при малом отношении u/cф (при малой окружной скорости).
Ступени, в которых при одном ряде СА преобразование кинетической энергии в механическую энергию вращения ротора производится в нескольких рядах рабочих лопаток, называются ступенями скорости.
Ступени скорости, 2х и 3х венечные (по числу рядов рабочих колес), используются в настоящее время в приводных турбинах небольшой мощности, для которых снижение габаритов и массы оказывается важнее экономичности (в авиации турбины со ступенями скорости применяются иногда для привода насосов жидкостных реактивных двигателей).
Рабочие лопатки ступеней скорости размещаются обычно на одном диске, который в этом случае в паротурбинной практике называется диском или колесом Кертиса.
Схема активной турбины с двумя ступенями скорости изображена на рис. 7.6.
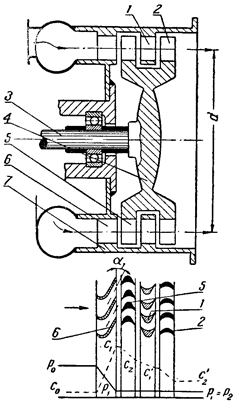
Рис. 7.6. Схема двухвенечной ступени скорости
В соплах 6 газ расширяется до конечного давления Р1 и поступает на рабочие лопатки 5 первой ступени. Так как ступень работает с величиной u/cф существенно меньшей оптимальной, то газ выходит из каналов рабочих лопаток 5 с большой скоростью с2. Это видно из рис. 7.7, где показаны треугольники скоростей ступени. Для использования выходной скорости газа поставлен второй ряд рабочих лопаток 2, а перед ними — ряд неподвижных направляющих лопаток 1. Последние не участвуют в преобразовании энергии; назначение их — подвести газ ко второму венцу рабочих лопаток под определенным углом. Конечно, скорость газа в направляющих лопатках вследствие неминуемых потерь падает от с2 до с’1. Треугольники скоростей второй ступени строятся так же, как и первой; буквенные обозначения скоростей и углов для второй ступени отличаются от обозначений первой ступени штрихом сверху.-
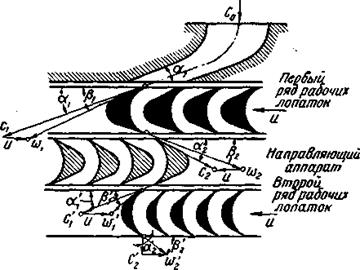
Рис. 7.7. Треугольники скоростей двухвенечной ступени скорости
Число ступеней скорости обычно ограничивают двумя, так как с увеличением числа ступеней падает КПД ступени — каждая ступень вносит в ее тепловой баланс новые потери в направляющих и рабочих лопатках (рис. 7.8).
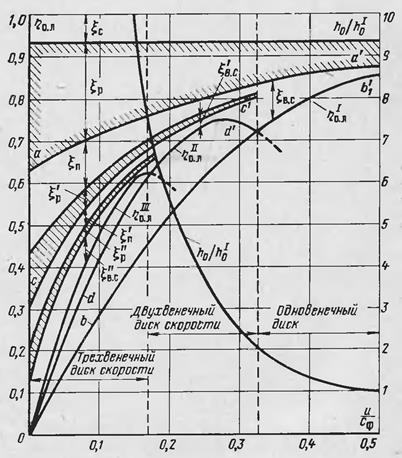
Рис. 7.8. Кривые относительного лопаточного КПД и потерь энергии в одновенечной активной ступени и ступенях скорости в зависимости от
На рис. 7.6 диск 4 откован заодно с валом 3. Сопла б и направляющие лопатки 1 укрепляются в корпусе турбины 7.
Ступени скорости выполняют только активными, допуская, однако, небольшую реактивность как в направляющих, так и в рабочих лопатках.
Найдем величину оптимального отношения u/cф для ступени скорости.
Для этого предположим, что турбина работает без потерь скорости в направляющих и рабочих лопатках и что лопатки симметричны, т. е. b1=b2; a2=a'1; b'1=b'2.
Тогда для двухвенечного диска треугольники скоростей, совмещенные так, как показано на рис. 7.9, образуют при минимальном значении выходной скорости с'2прямоугольный треугольник со сторонами с1,4и, с'2. Из треугольника следует, что
4u=c1cos a1,
откуда (при условии, что для чисто активной ступени без потерь c1=cф)
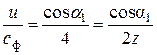
или, приводя в более общий вид:
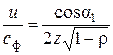 .
.
где z — число ступеней.
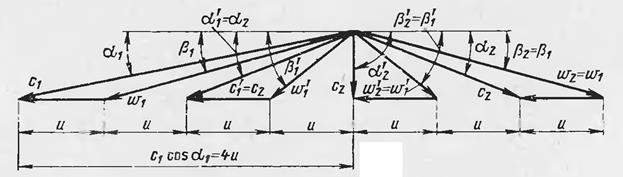
Рис. 7.9. Треугольники скоростей двухвенечной ступени для случая отсутствия скоростей
Строя аналогичным образом треугольники скоростей для ступени с тремя и более рядами рабочих колес, легко доказать справедливость выведенной формулы.
Таким образом при данном тепловом перепаде окружная скорость колеса Кертиса обратно пропорциональна числу рядов рабочих лопаток.
В заключении можно отметит, что оптимальное отношение u/cф для двух венечной ступени составляет 0,25, а для трехвенечной 0,17. Это означает, что оптимальное значение теплоперепада для двухвенечной ступени в 4 раза больше, чем для одновенечной активной, а для трехвенечной – в 9 раз. Естественно, что КПД при этом снижается (см. рис. 7.8).
Дата добавления: 2015-06-17; просмотров: 7284;
