Тема № 4: Основные уравнения газового потока в лопаточных машинах

Преобразование энергии расширения рабочего тела в энергию вращения ротора происходит в результате обтекания потоком неподвижных сопловых и рабочих решеток.

Законы течения сжимаемой жидкости имеют большое значение для изучения процессов, происходящих в ступени.

Теория лопаточных машин базируется на основных уравнениях движения газа: уравнении неразрывности, уравнении сохранения энергии, уравнении первого закона термодинамики, уравнении Бернулли и уравнениях Эйлера. Эти уравнения рассматриваются в курсе термодинамики. Здесь остановимся лишь на некоторых особенностях этих уравнений, которые связаны с их использованием в расчетах лопаточных машин. Уравнение Эйлера о количестве движения применительно к ступени турбины будет рассмотрено ниже.

Реальное течение рабочего тела в ступени турбомашины является пространственным периодически неустановившимся течением вязкого сжимаемого газа, математическое исследование которого в строгой постановке затруднительно. Для получения относительно простых уравнений, которые можно без труда использовать в инженерных расчетах, делаются некоторые упрощения:

1) рассматривают осредненные значения параметров в точке (стационарность);

2) во всех сечениях каждой ступени неизменными.

Указанные допущения означают, что число лопаток СА и РК бесконечно.

Уравнение неразрывности

Уравнение неразрывности в случае установившегося течения формулируется следующим образом: секундный массовый расход газа через любое поперечное сечение элементарной струйки при установившемся течении сохраняется постоянным (см. рис. 4.1).

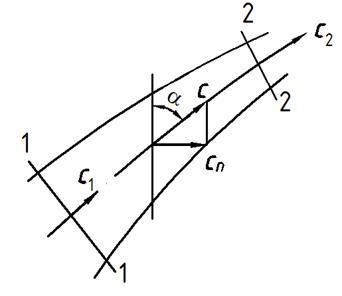
Рис. 4.1. К выводу уравнения неразрывности

Если в рассматриваемых сечениях элемента двигателя поток является равномерным или рассматриваются осредненные параметры газового потока в этих сечениях, то уравнение неразрывности с равным основанием может быть записано и для всего потока. В частности, для сечений, нормальных к оси потока:

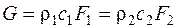. (2.1)

В общем случае, когда выбранное сечение не перпендикулярно к оси струйки, а составляет с ней некий угол 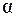, нужно рассматривать нормальную составляющую скорости в этом сечении 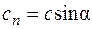(т. е. в применении к теории ступени турбомашин – осевую составляющую скорости 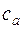), а уравнение неразрывности записывается в виде:

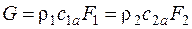. (2.2)

Уравнение первого закона термодинамики

Уравнением первого закона термодинамики пользуются для определения параметров состояния газа при осуществлении термодинамического процесса. Оно является частным выражением закона сохранения энергии для элементарного объема газа, написанным в системе координат, движущейся вместе с рассматриваемым элементом объема или, в частном случае, для покоящегося газа.

Для элементарного объема газа уравнение первого закона термодинамики имеет вид:

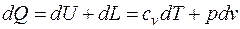, (2.7)

т. е. все тепло, подведенное к рассматриваемому объему газа, идет на изменение внутренней энергии 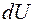и на совершение работы 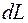против сил давления, связанной с изменением объема.

Для движущегося газа удобно вместо внутренней энергии пользоваться понятием энтальпии:

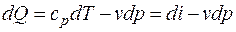. (1.8)

Переходя к интегральной форме записи, с учетом того, что тепло трения эквивалентно работе сил трения 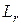, можно получить:

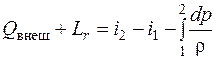, (1.9)

т. е. все тепло, подводимое к потоку между сечениями 1–1 и 2–2 (рис. 2.2), состоящее из тепла, подводимого извне, и тепла, выделяющегося в результате трения (работы сил трения), идет на совершение работы сжатия (расширения) 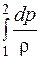и на изменение внутренней энергии потока ( ).

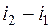Уравнение первого закона термодинамики удобно для определения работы сил трения по известному значению показателя политропы 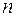, который легко определяется по термодинамическим соотношениям, если известны параметры потока в начале и в конце процесса.

Обобщенное уравнение Бернулли

Основным уравнением, на котором строятся расчеты турбомашин, является уравнение Бернулли:

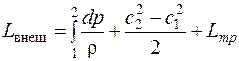. (2.10)

Уравнение (2.10) можно трактовать так: подведенная извне энергия 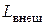идет на работу сжатия (расширения) газа 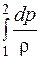, приращение кинетической энергии 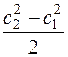и преодоление гидравлического сопротивления .

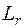Заметим, что уравнение Бернулли не зависит от теплообмена с окружающей средой. Однако теплообмен оказывает косвенное влияние на показатель политропы процесса.

Уравнение Бернулли, как и уравнение сохранения энергии, можно отнести к энергетическим и получить его из рассмотрения баланса механической энергии.

При свободном движении идеального газа, при отсутствии энергии, подведенной извне и потерь на преодоление гидравлического сопротивления:

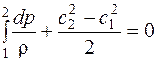. (1.11)

Для идеальной несжимаемой жидкости, для которой :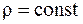

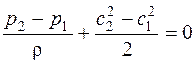, (1.12)

т. е. для повышения давления в компрессоре динамического действия необходимо затормозить поток.

Самый простой способ достичь этого – геометрическое воздействие:

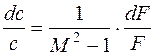, (1.13)

Таким образом, при дозвуковом потоке ( 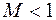) расширение канала приводит к снижению скорости потока. На замедляющийся поток набегают следующие молекулы, что приводит к снижению удельного объема (увеличению плотности), т. е. давление газа растет.

Можно сделать вывод, что рабочий процесс турбокомпрессора состоит из двух взаимосвязанных, одновременно протекающих процессов:

- приращения кинетической энергии 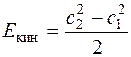за счет подводимой внешней работы (от турбины) ;

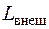- преобразования кинетической энергии потока 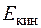в энергию потенциальную 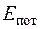, пропорциональную давлению.

Уравнение сохранения энергии

Полная энергия рабочего тела 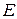может быть записана в виде:

,

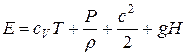где 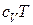-- внутренняя энергия; P/r – потенциальная энергия давления; С²/2 – кинетическая энергия; 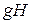-- потенциальная энергия положения.

Данное выражение можно упростить.

Потенциальной энергией положения 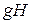можно пренебречь, т.к. по сравнению с остальными слагаемыми она ничтожна.

Внутренняя энергия рабочего тела 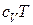в сумме с потенциальной энергией давления P/r будут равны энтальпии рабочего тела h, которая, таким образом, является мерой той потенциальной энергии, которой обладает поток рабочего тела.

В этом случае уравнение полной энергии запишется в виде:

.

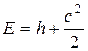Уравнение сохранения энергии может быть сформулировано следующим образом: полная энергия газового потока на выходе 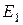из рассматриваемого элемента (рис. 4.2) больше (или меньше) полной его энергии на входе 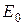на величину энергии, подведенной (или отведенной) между рассматриваемыми сечениями :

.

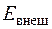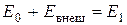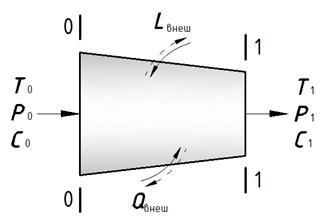
Рис. 4.2. К выводу уравнения сохранения энергии

Поскольку при установившемся движении газа расходы через сечения 0–0 и 1–1 одинаковы, то все члены уравнения сохранения энергии принято представлять отнесенными к 1 кг газа.

Применительно к турбомашинам уравнение сохранения энергии можно записать в виде:

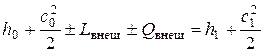, (2.3)

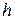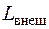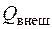где – энтальпия газа (отвечает за внутреннюю и потенциальную энергию потока), с²/2 – кинетическая энергия потока; и – внешняя подведенная (отведенная) энергия, в виде механической работы и в виде тепла соответственно.

Для элементов двигателя, в которых отсутствует подвод или отвод энергии, уравнение сохранения энергии в частном случае имеет вид:

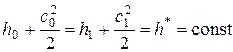, (2.4)

т. е. при отсутствии энергообмена полная энергия газового потока сохраняется неизменной и равна энтальпии заторможенного потока.

Запишем уравнение сохранения энергии для турбинной ступени (см. рис. 2.1). Теплообменом с окружающей средой при этом можно пренебречь, т.к. при относительно небольших площадях теплоотдачи и хорошей теплоизоляции коэффициенты теплоотдачи малы.

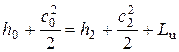
или

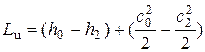
Обычно для турбинной ступени 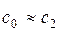, поэтому

,

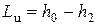т.е. работа турбинной ступени фактически численно равна изменению энтальпии потока.

Заметим, что в различные записи уравнения сохранения энергии в явном виде не входит трение, а значит, это уравнение применимо как для идеального газа, так и газа, обладающего вязкостью.

Силы трения, которые возникают на стенках, ограничивающих поток газа, и силы внутреннего трения между отдельными струйками газа являются внутренними силами, а работа на их преодоление переходит практически полностью в тепло. Трение приводит лишь к преобразованию одного вида энергии в другой и не отражается на общем балансе энергии. Например, если вследствие трения уменьшается кинетическая энергия, то энтальпия в этом сечении вырастет на ту же величину.