Тема № 5: Течение рабочего тела в каналах турбинной решетки

Расширение рабочего тела в каналах соплового аппарата

Рассмотрим применение основных уравнений движения сжимаемой жидкости на примере истечения газа из сопел (рис. 5.1).

Это впоследствии поможет нам лучше понять механизм работы ступени, кроме того введем несколько чрезвычайно важных понятий, которые используются в теории ступени турбомашин.

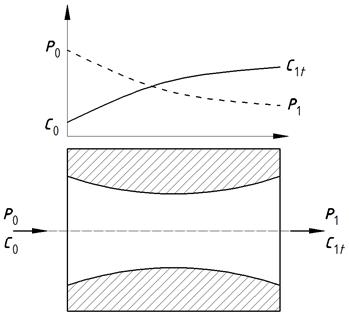
Рис. 5.1. Истечение газа из сопла

Запишем уравнение сохранения энергии для истечения идеального газа из сопла:

,

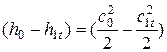т.е. изменение кинетической энергии определяется изменением энергии потенциальной при отсутствии теплообмена с окружающей средой.

Учитывая уравнение состояния идеального газа

,

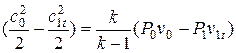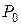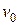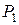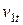где и -- давление и удельный объем рабочего тела в начале процесса расширения; и -- давление и удельный объем рабочего тела в конце процесса расширения (теоретического).

При такой записи уравнения сохранения энергии не нужно знать закон изменения состояния потока, а только начальное и конечное состояние рабочего тела.

Зная 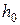и 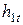, а также 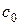можно найти скорость рабочего тела на выходе из сопла:

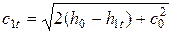
При отсутствии потерь процесс расширения в сопле пойдет по изоэнтропе (s=const). Зная давление в конце процесса расширения 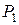можно найти энтальпию рабочего тела в конце процесса расширения 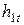, а значит и теоретическую (максимально достижимую) скорость на выходе из сопла в .

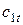Процесс расширения газа в сопле принято изображать на h –s – диаграмме (см. рис. 5.2).

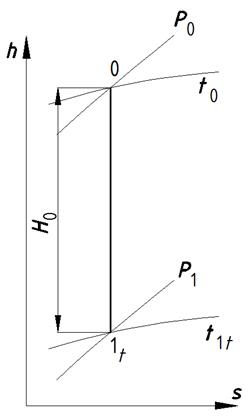
Если скоростью 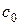можно пренебречь, то .

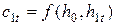Если же скоростью 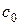пренебречь нельзя, то можно сделать предложение, что кинетическая энергия на входе в сопло возникла в результате изоэнтропийного расширения рабочего тела от некоторых параметров 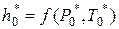, при которых начальная скорость была равна нулю. до начальных параметров 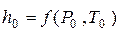. Или 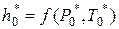-- это параметры, которые бы имел бы поток с начальными параметрам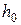и и 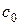при изоэнтропийном торможении до скорости равной нулю.

Поэтому параметры 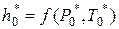принято называть параметрами торможения (параметрами заторможенного потока).

При построении процесса в h –s – диаграмме необходимо отложить от точки 0 вверх по изоэнтропе отрезок равный 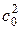/2 (рис. 5.3).

После введения понятия полных параметров можно записать:

,

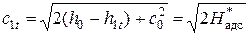где 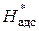-- адиабатический (располагаемый) теплоперепад на сопло, отсчитанный от полных параметров.

Теплоперепадом называют разницу энтальпий на входе и выходе из некого устройства (сопло, рабочее колесо, ступень, турбина и т.д.), которая показывает снижение внутренней энергии и фактически, как мы уже знает, равна работе, совершаемой данным устройством.

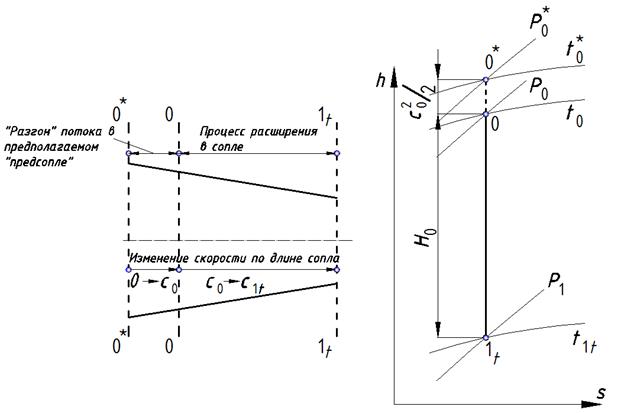
Рис. 5.3. К пояснению понятия «заторможенные параметры потока»

Если скорость потока 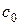невелика, что часто имеет место в турбомашинах, то для вычисления параметров торможения можно воспользоваться следующими соотношениями:

,

,

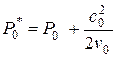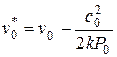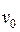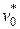где и -- удельный объем рабочего тела в начале процесс по статическим и полным параметрам, соответственно; 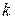-- показатель адиабаты.

До сих пор мы говорили о расширении в сопле идеального газа, в котором отсутствует взаимодействие между молекулами (отсутствует вязкость. При взаимодействии такого газа с поверхностями, образующими канал сопла не возникает пограничного слоя, т.е. отсутствуют потери на трение.

Этого нельзя сказать о реальном газе. Пограничный слой, который образуется при обтекании реальным газом следствие возникающих потерь приводит к снижению проходного сечения сопла и, как следствие, снижению расхода рабочего тела через сопло. Отношение действительного расхода рабочего тела 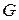к теоретическому 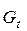называют коэффициентом расхода :

.

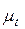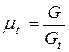Коэффициент расхода достаточно высок для сопел и составляет 0,95…0,97.

При истечении идеального рабочего тела из сопла вся внутренняя энергия рабочего тела преобразуется в кинетическую. В действительности часть энергии рассеивается и в виде тепла сообщается рабочему телу. Вследствие этого энтальпия рабочего тела на выходе из сопла несколько возрастает до значения 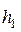. Истинная кинетическая энергия же (скорость потока 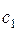) на выходе из сопла будет меньше, чем подсчитанная выше скорость .

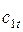Для сравнения реального процесса с теоретическим используют понятие коэффициент скорости :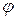

.

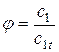Коэффициент скорости для сопел также достаточно высок и достигает значений 0,95…0,98.

Теперь мы можем достроить диаграмму расширения газа в сопле.

Расширение в реальном процессе также пойдет до давления 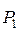до точки 1. При изображении реального процесса расширения рабочего тела в h – s – диаграмме кривая процесса отклоняется вправо. Это отклонение будет тем больше, чем выше будет уровень потерь в сопле (см. рис. 5.4).

Тогда для реального рабочего тела уравнение сохранения энергии можно записать между точками 0 и 1:

.

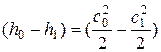Также можно записать:

Dh_c= .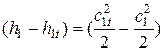

Величина Dh_c – будет обозначать потери в соплах.

Используя понятие коэффициента скорости, выражение для величины потерь в соплах возможно преобразовать:

Dh_c= .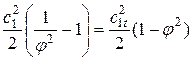

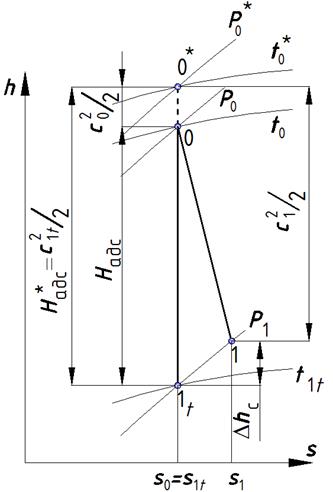
Рис. 5.4. Процесс истечения рабочего тела из сопла в h-s – диаграмме

Однако чаще удобнее пользоваться не абсолютными значения потерь, а относительными. Для этого потери в соплах необходимо разделить на теплоперепад сопла:

.

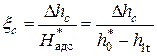Коэффициент потерь в соплах связан с коэффициентом скорости сопла. Пропуская некоторые несложные преобразования, можно записать:

.

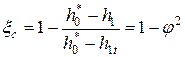В заключении необходимо отметить, что коэффициент потерь 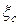характеризует совершенство сопла как отдельно взятого устройства. Совершенство сопла в составе ступени будет характеризовать другой коэффициент.

Расширение рабочего тела в каналах рабочей решетки

Все выкладки, приведенные в предыдущем разделе для соплового аппарата, имеют силу и для расширения рабочего тела в рабочей решетке.

Однако существуют и свои особенности.

Диаграмма расширения для каналов рабочей решетки строится не по абсолютным скоростям потока, а по относительным.

Расширение рабочего тела в РК начинается в точке 1 (см. рис. 5.5). При отсутствии потерь (рабочее тело – идеальный газ) процесс пойдет по изоэнтропе в точку 2t до давления .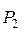

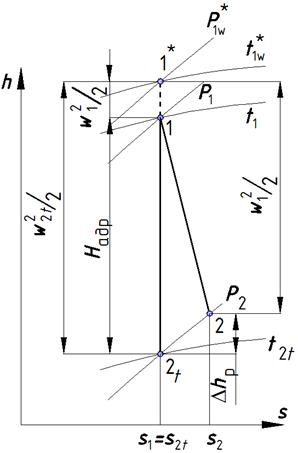
Рис. 5.5. Процесс расширения рабочего тела в рабочих решетках
в h-s – диаграмме

Для теоретического процесса расширения будет справедлива следующая запись уравнения сохранения энергии:

,

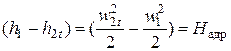где 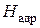-- располагаемый теплоперепад на рабочее колесо.

При расширении реального газа часть энергии также будет рассеиваться в тепло, что приведет к росту энтальпии рабочего тела в конце процесса расширения, а реальная скорость 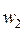будет меньше теоретической .

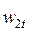Несовершенство течения в рабочем колесе принято характеризовать коэффициентом скорости :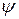

.

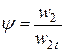Коэффициент скорости для рабочего колеса несколько ниже, чем в соплах, вследствие турбулизации потока за сопловым аппаратом, а также за счет вращения рабочего колеса и достигает значений 0,93…0,96.

Расширение в реальном процессе пойдет до давления 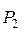в точку 2. При изображении реального процесса расширения рабочего тела в h – s – диаграмме кривая процесса отклоняется вправо. Это отклонение будет тем больше, чем выше будет уровень потерь в рабочем колесе.

Для реального процесса можно записать:

.

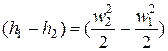Потери в рабочем колесе будут равны:

Dh_р= .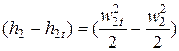

Используя понятие коэффициента скорости, выражение для величины потерь в рабочем колесе возможно преобразовать:

Dh_р= .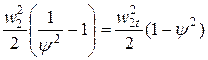

Как и для сопел введем понятие относительных потерь:

.

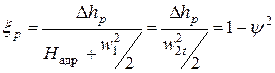Коэффициенты скорост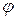и и 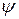определяются качеством проектирования и изготовления соплового аппарата и рабочего колеса. Они показывают насколько реальный поток близок к теоретическому.

Потери с выходной скоростью

Мы уже знаем, что вследствие вязкости рабочего тела при обтекании потоком сопловых и рабочих лопаток возникают потери на трение, которые приводят к некоторой недовыработке ступенью располагаемой работы.

Однако в ступени существует еще одна потеря, связанная с тем, что поток, уходя со ступени, имеет некоторую скорость .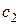

Вместе с этой скоростью из ступени уходит часть энергии равная 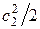, которая не может быть использована в ступени. Она получила название потеря с выходной скоростью:

.

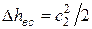Наличие потери с выходной скоростью приводит к уменьшению полезной работы ступени, что, естественно, снижает КПД ступени.

В многоступенчатых турбинах энергия 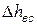может быть использована в последующих ступенях, но об этом мы поговорим позже.

Для потерь в соплах и рабочих решетках, которые были рассмотрены ранее характерно увеличение энтропий, что связано с переходом части энергии в тепло. Для потери с выходной скоростью 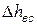это, естественно, неверно, поэтому увеличения энтропии не происходит (рис. 5.6).

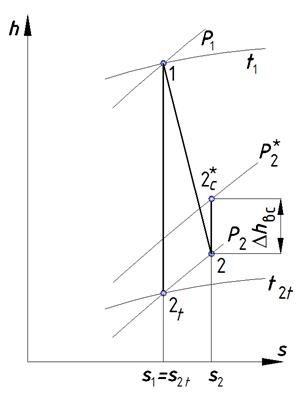
Рис. 5.6. Изображение потерь с выходной скоростью на h-s – диаграмме

Изображение процесса расширения рабочего тела в ступени в h-s – диаграмме

Рассмотрев по отдельность процессы расширения в элементах турбинной ступени и потери, которые при этом возникают, мы можем легко изобразить процесс расширения рабочего тела в ступени в h-s – диаграмме. Для этого надо совместить рис. 5.4-5.6. на одной диаграмме (см. рис. 5.7).

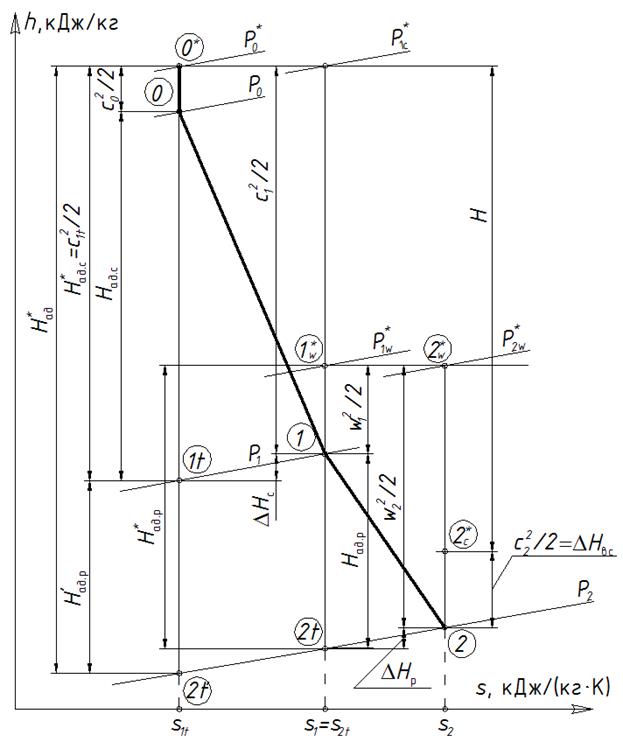
Рис. 5.6. Ход процесса расширения рабочего тела в ступени на i-S диаграмме

На общей диаграмме расширения рабочего тела в ступени есть ряд особенностей, которые было невозможно изобразить при раздельном рассмотрении процесса расширения.

1. Кривая процесса расширения рабочего тела в реальном процессе в рабочей решетке (линия 1-2) более пологая, чем для соплового аппарата (линия 0-1), что связано с более высоким уровнем потерь в рабочей решетке.

2. В силу того, что изобары на h-s – диаграмме расходятся незначительно, можно говорить о том, что отрезки между точками 1-2t и 1-2t’ равны между собой. Если расстояние между точками 1-2t – эторасполагаемый теплоперепад на рабочее колесо 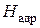, то расстояние между точками 1-2t’ принято обозначать 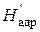. Естественно, что .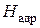

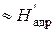3. После сделанных преобразований на h-s – диаграмме хорошо видно, что

,

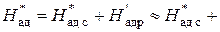
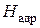т.е. располагаемый теплоперепад ступени, отсчитанный от полных параметров, будет равен сумме располагаемых теплоперпадов на сопловой аппарат и рабочее колесо.

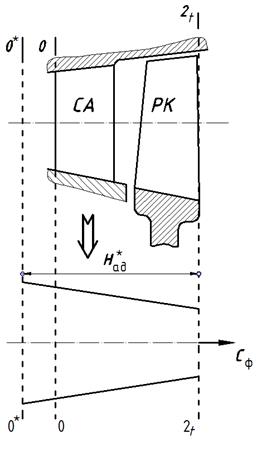
4. Расстояние между точкам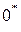и и 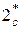обозначено Н и равно работе ступени (сработанному теплоперепаду).

Понятие фиктивной скорости

Для дальнейшего изложения теории ступени турбомашины необходимо ввести еще одно важнейшее понятие.

Представим, что рассматриваемую ступень, состоящую из соплового аппарата и рабочего колеса, мы меняем на эквивалентное сопло. При этом теплоперепад на эквивалентное сопло равен теплоперепаду на ступень, отсчитанному от параметров торможении 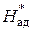(рис. 5.7).

Тогда при срабатывании теплоперепада 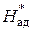на выходе из эквивалентного сопла в адиабатическом процессе скорость потока составит:

,

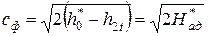где 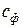-- фиктивная скорость.

Фиктивная скорость не имеет физического смысла – это искусственно введенный параметр, но при этом является важнейшей характеристикой ступени – она характеризует теплоперепад, приходящийся на ступень, или другими словами работу, которую можно получить со ступени.

Понятие степени реактивности

Мы уже знаем, что в турбинной ступени происходит преобразование потенциальной энергии пара сначала в кинетическую энергию струй потока, а затем в механическую энергию вращения ротора. При этом общий теплоперепад ступени делится между сопловым аппаратом и рабочим колесом:

,

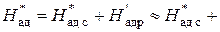
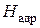Пропорции, в которых происходит это разделение можно увидеть при рассмотрении h-s – диаграммы расширения рабочего тела в ступени.

Для качественного описания этих соотношений вводится понятие степени реактивности ступени.

Степенью реактивности ступени называют отношение располагаемого теплоперепада на рабочую решетку к суммарному адиабатическому теплоперепаду всей ступени, подсчитанному от параметров торможения:

.

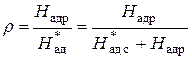Степень реактивности показывает какая доля располагаемого теплоперепада ступени срабатывается в ее рабочих каналах.

Название связано с тем, что при расширении рабочего тела в рабочих каналах поток ускоряется и возникает дополнительная реактивная сила, которая передает дополнительный импульс вращению ротора.

Понятие степени реактивности согласно тому определению, которое было дано выше, является термодинамической характеристикой ступени, поэтому оценивать ступень по данному понятию удобнее всего по h-s – диаграмме расширения рабочего тела в ступени (рис. 5.8 б).

По значению степени реактивности выделяют 2 типа ступеней:

- активные – со степень реактивности 0…0,25;

- реактивные – со степенью реактивности 0,25…0,50.

При этом в чисто активной ступени степень реактивности r=0 – все расширение рабочего тела происходит в сопловом аппарате, а в рабочем колесе осуществляется только разворот потока (h-s – диаграмма показана на рис. 5.8 а).

В чисто реактивной ступени (r=0.5) теплоперепад поровну делиться между сопловым аппаратом и рабочим колесом, т.е. 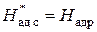(h-s – диаграмма показана на рис. 5.8 в).

Деление ступеней на активные и реактивные довольно условно и справедливо в полной мере лишь для ступеней с малой верностью ( 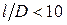). Для ступеней с более высокими лопатками характерно значительно изменение степени реактивности по высоте (от ~0,05 в корне и до 0,6…0,7 на периферии), что не позволяет использовать характеристики «активная» или «реактивная».

а. б. в.

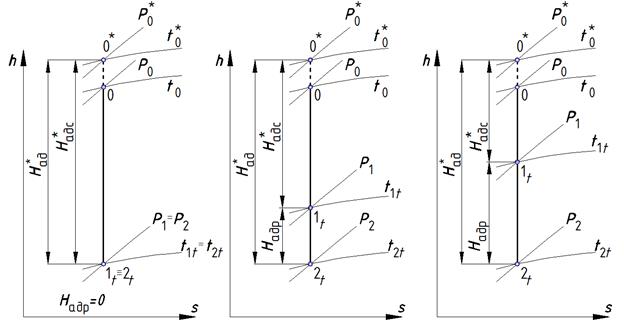
Рис. 5.8. Диаграммы расширения для ступеней различного типа: а. – чисто активная ступень; б. – общий случай; в. – ступень чисто реактивного типа

Помимо термодинамической степени реактивности существует понятии кинематической степени реактивности, которая подсчитывается по кинематическим параметрам (компонентам треугольников скоростей ступени):

.

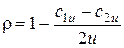Активный и реактивный принцип преобразования энергии в турбинной ступени

После того, как мы дали определение степени реактивности и более четко разделили ступени на активные и реактивные, необходимо чуть подробнее остановиться на некоторых отличиях в активном и реактивном принципах преобразования энергии в ступенях.

Рассмотрим 2 крайних случая: чисто активную и чисто реактивную ступени – и изобразим схемы ступеней данных типов и графики изменения параметров по длине их проточной части (см. рис. 5.9).

Какие-либо комментарии к рис. 5.9 являются, в данном случае, излишними. Студентам предлагается провести самостоятельный анализ данного рисунка на основании тех знаний, которые они приобрели в ходе предыдущих лекций.

а. б.

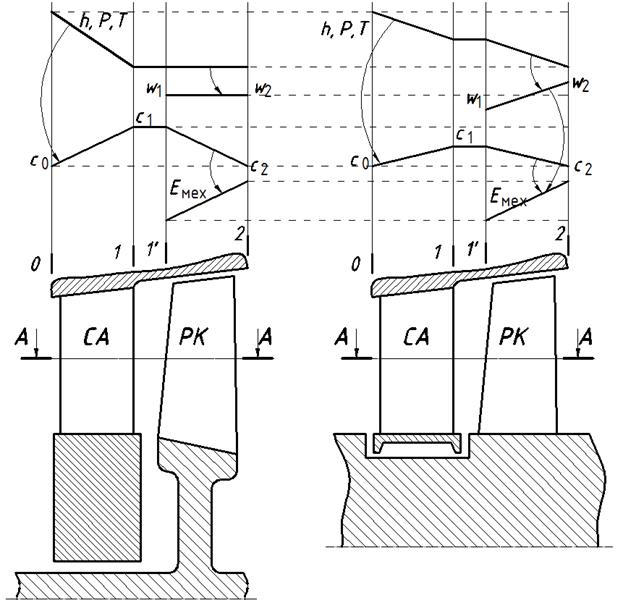
Рис. 5.9. Активный (а) и реактивный (б) принципы преобразования энергии в турбинных ступенях

На рис. 5.10 показаны лопаточные профили и треугольники скоростей. Отметим некоторые их особенности:

- В рабочей решетке ступени активного типа не происходит расширения рабочего тела, поэтому межлопаточный канал имеет постоянное проходное сечение. Это определяет следующие соотношения в треугольниках скоросте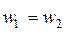й: и .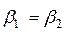

- С ступени реактивного типа расширение рабочего тела происходит в равной степени в сопловом аппарате и рабочем колесе, поэтому профили СЛ и РЛ конгруэнтны, т.е. имеют одинаковую форму, но развернуты под разными углами. Треугольники скоростей в свою очередь, симметричны, а соотношения кинематических параметров следующие: 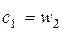, , 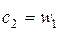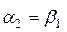и .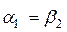

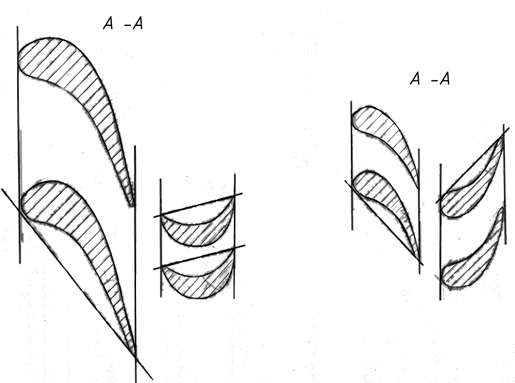
Рис. 5.10. Профили лопаточного аппарата и треугольники скоростей активной (а) и реактивной (б) турбинных ступеней

Диаграммы расширения рабочего тела для обоих типов ступеней были показаны на рис. 5.8.

Таким образом, тип ступени предопределяет конструкцию ступени и турбины, кинематические и термодинамические соотношения в ступени, форму профиле и др.

Особенности проектирования ступеней и глубокие конструктивные различия меду ступенями двух типов таковы, что завод, специализирующийся на турбинах активного (реактивного) типов исключительно редко способен выпускать турбины второго типа.