Относительный покой жидкости: вращение цилиндрического сосуда с жидкостью с постоянной угловой скоростью

При вращении сосуда вокруг вертикальной оси 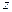(рис. 2.7) на любую частицу жидкости кроме силы тяжести действует также центробежная сила инерции:

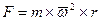, (2.24)

которую можно разложить на составляющие:

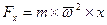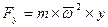и , (2.25)

где 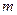- масса частицы;

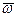- угловая скорость;

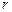- расстояние частицы от оси вращения;

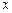и 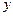- проекции вектора 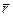на координатные оси, причем .

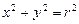Следовательно, проекции ускорения массовых сил на координатные оси в рассматриваемом случае равновесия жидкости равны:

, , .

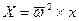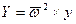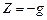Подставив эти значения 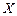, 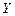и 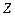в дифференциальное уравнение равновесия (2.6) получим:

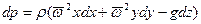, (2.26)

откуда после интегрирования имеем:

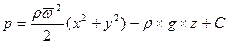. (2.27)

Полагая, что начало координат находится на поверхности жидкости и давление здесь равняется , получим получим:

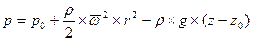. (2.28)

где 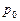- давление на свободной поверхности;

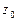- вершина параболоида вращения.

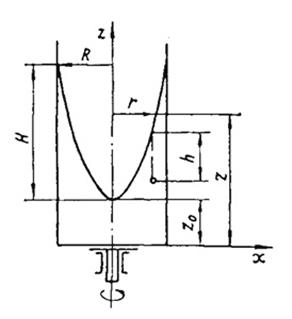
Рисунок 2.7 Вращение резервуара с жидкостью

В произвольной точке, расположенной на глубине 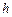под поверхностью жидкости, давление:

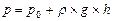. (2.29)

Поверхности уровня представляют собой параболоиды вращения. Уравнение свободной поверхности жидкости имеет вид:

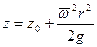. (2.30)

Пьезометрическая поверхность при 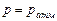совпадает со свободной поверхностью жидкости. Если свободная поверхность отсутствует (закрытый сосуд полностью заполнен жидкостью под давлением), то пьезометрическая поверхность проходит через точку жидкости, в которой давление равно атмосферному (например, через уровень в открытом пьезометре, где ).

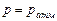Если 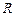- радиус сосуда, а 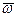- угловая скорость, то высота параболоида вращения:

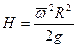. (2.31)

Объем параболоида вращения:

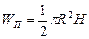. (2.32)