Момент импульса и закон его сохранения

Моментом импульса (количества движения) материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением:

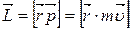, (4.13)

где 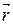– радиус-вектор, проведенный из точки О в точку A; 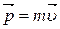– импульс материальной точки (рис. 4.8); 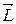–вектор, направленный по оси вращения в соответствии с правилом правого винта.

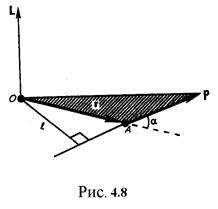Модуль вектора момента импульса

,

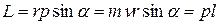где 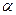– угол между векторами 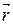и , l – плечо вектора относительно точки О. При 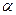=90º

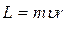, (4.14)

Момент импульса можно выразить через момент инерции 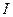и угловую скорость 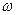, т.е.

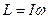. (4.15)

Таким образом, момент импульса твердого тела относительно оси равен произведению момента инерции тела относительно той же оси на угловую скорость.

Продифференцируем уравнение (4.15) по времени:

,

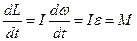или

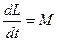. (4.16)

Это выражение – основное уравнение динамики вращательного движения твердого тела относительно неподвижной оси: производная по времени момента импульса твердого тела относительно оси равна моменту сил относительно этой же оси.

Можно показать, что имеет место векторное равенство

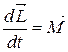. (4.17)

В замкнутой системе момент внешних сил 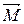= 0 и 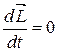, откуда

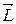= const. (4.18)

Выражение (4.18) представляет собой закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т.е. не изменяется с течением времени.

Закон сохранения момента импульса – фундаментальный закон природы. Он связан со свойством симметрии пространства – его изотропностью, т.е. с инвариантностью физических законов относительно выбора направления осей координат системы отсчета (относительно поворота замкнутой системы в пространстве на любой угол).