МЕТОД КОМПЛЕКСНЫХ ЧИСЕЛ

Для расчета цепей переменного тока, а также для анализа процессов в электрических машинах широкое применение получил так называемый символический метод, основанный на использовании комплексных чисел.

Как известно, комплексное число 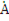(рис.231 ) может быть записано в трех формах: алгебраической, тригонометрической и показательной:

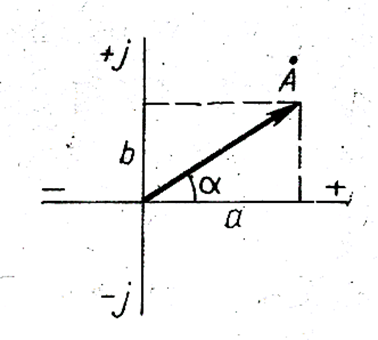
Рис.231

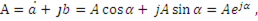(п.6)

где 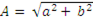- модуль комплексного числа;

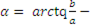аргумент показывающий ориентировку вектора на числовой плоскости, и .

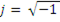Если аргумент 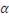изменяется со временем, например 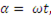то точка на числовой плоскости, соответствующая комплексному числу 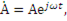описывает окружность радиуса А с центром в начале координат. Поэтому комплексное число 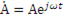может быть представлено вектором 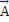, вращающимся против часовой стрелки с угловой скоростью ω. Эта особенность комплексных чисел и дает возможность применять их к гармонически изменяющимся величинам.

Сложение и вычитание комплексных чисел. Для сложения и вычитания комплексных чисел они должны быть представлены в алгебраической форме. При сложении складываются отдельно их действительные и мнимые части, например

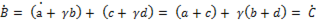+ (п.7)

Так как каждое комплексное число может быть представлено вектором, то сложению двух комплексных чисел соответствует сложение двух векторов.

Вычитание комплексных чисел может быть заменено сложением уменьшаемого числа с вычитаемым, взятым с обратным знаком, что следует из выражения

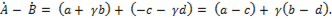(п.8)

Умножение и деление комплексных чисел. Умножение и деление комплексных чисел проще всего производится в том случае, когда они выражены в показательной форме.

Допустим, что нужно перемножить два комплекса, выраженных через свои модули А и В и аргументы 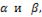т.е.

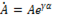и 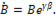В результате получается новый комплекс

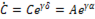
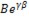= (п.9)

откуда следует . что 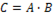и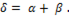

Произведение двух комплексов дает новый комплекс, модуль которого равен произведению модулей множителей, а аргумент равен алгебраической сумме аргументов перемножаемых комплексов.

Частное от деления комплекса 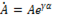на комплекс 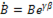равно

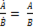
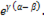(п.10)

Частное от деления одного комплекса на другой дает новый комплекс, модуль которого равен частному от деления модуля делимого на модуль комплекса делителя, а аргумент равен алгебраической разности аргументов делимого и делителя.

Напряжения и токи в комплексном виде. Любая синусоидальная функция может быть представлена комплексным числом.

Расчет электрических цепей переменного тока может быть значительно облегчен, если использовать комплексные числа для обозначения электрических величин. При представлении этих величин в комплексном виде все формулы, законы и методы расчетов цепей постоянного тока применимы и для цепей переменного тока.

Если напряжение 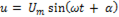, то вектор этого напряжения имеет длину, равную действующему значению 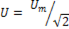и угол наклона вектора к оси абсцисс равен 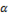. Этот же вектор может быть выражен комплексным числом с модулем , равным действующему значению, а аргументом – начальной фазе. Таким образом,

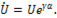(п.11)

Если 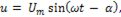то

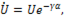(п.12)

если 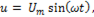то

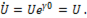(п.13)

Переводя выражение в алгебраическую форму записи, получим

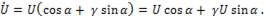(п.14)

Так как 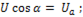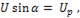то

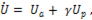(п.15)

т.е. вещественная часть комплексного числа – это активная составляющая напряжения, а мнимая часть - его реактивная составляющая. Аналогично для уравнения ( )

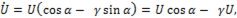(п.16)

или

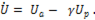(п.17)

Знак плюс у реактивной составляющей означает индуктивный, а знак минус - емкостной характер цепи.