ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
В современной практике чаще используются переменные токи, т.к. в сравнении с постоянными токами они обладают рядом существенных преимуществ:
- Изготовление генераторов и двигателей переменного тока экономически, а зачастую и технически более выгодно в сравнении с генераторами и двигателями постоянного тока.
- Переменный ток легко трансформируется.
- Переменный ток легко преобразуется в постоянный.
Переменными называют токи (напряжение, эдс), меняющийся во времени.
Эти величины с течением времени могут изменяться только по величине (рис.61 а)
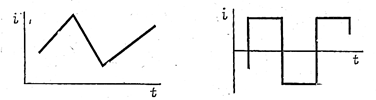
а б
Рис.61
или по направлению (рис. 61б), а также и по величине, и по направлению по различным
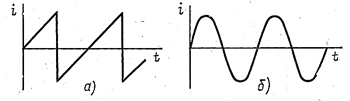
Рис.62
законам (рис.62 а,б).
В практике среди переменных токов наибольшее распространение получили синусоидальные токи благодаря следующим преимуществам:
- При подаче синусоидального сигнала на обмотки трансформатора, на его выходе напряжение остается синусоидальным, т.е. сигнал при преобразовании не искажается;
- Использование несинусоидальных токов в электротехнических устройствах, а также при электропередаче приводит к дополнительным электрическим потерям;
- Синусоидальные токи, напряжения, эдс при анализе и расчетах легко поддаются математической обработке, т.к. синусоидальная функция – функция, имеющая подобную себе производную.
Синусоидальным переменным током (напряжением, эдс) называется такой периодический ток, который изменяет свое направление и величину по закону синуса или косинуса.
Аналитически зависимость тока от времени можно представить выражением:
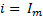
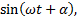 (5-1)
(5-1)
где 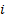 - мгновенное значение тока,
- мгновенное значение тока, 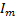 – максимальное или амплитудное значение тока; аргумент функции (𝜔𝑡+𝛼) называется фазой, отсчитываемой от точки перехода тока через нуль к положительному значению; α – начальная фаза – значение фазы синусоидального тока в начальный момент времени.
– максимальное или амплитудное значение тока; аргумент функции (𝜔𝑡+𝛼) называется фазой, отсчитываемой от точки перехода тока через нуль к положительному значению; α – начальная фаза – значение фазы синусоидального тока в начальный момент времени.
Так как синусоидальной функцией можно описать вращательное движение, то под угловой частотой ω понимают скорость изменения переменной величины, где путь 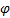 , пройденный этой переменной, выражен в радианах.
, пройденный этой переменной, выражен в радианах.
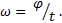
Откуда следует, что
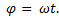 (5-2)
(5-2)
При 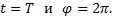 Тогда
Тогда 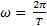 =
= 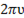 , где
, где 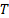 - период, а ʋ = 1/T –частота колебаний. Период измеряется в секундах (с), а частота в герцах (Гц).
- период, а ʋ = 1/T –частота колебаний. Период измеряется в секундах (с), а частота в герцах (Гц).
Графическое изображение синусоидальных величин. Графически синусоидально изменяющиеся функции изображаются синусоидами (рис.63 а) или вращающимися векторами (рис. 63б). В первом случае (временная диаграмма) ординаты синусоиды представляют
 Рис.63
Рис.63
собой мгновенные значения функции, а абсциссы – промежутки времени или фазы. Синусоида наглядно отражает изменения переменной величины во времени. Во втором случае (векторная диаграмма) длина вращающегося вектора отражает амплитуду, а угол, образованный этом вектором и осью абсцисс – фазу переменной. Проекции вращающегося вектора на ось ординат определяют мгновенные значения переменной.
При анализе цепей переменного тока, в большинстве случаев, нужно определять действующие значения токов (напряжений, эдс) и сдвиги фаз между ними. Для этой цели достаточно построения векторных диаграмм токов и напряжений соответствующих цепей. Такие диаграммы строятся для неподвижных векторов, т.е. векторы напряжений и токов цепи рассматриваются в положении, которое они занимают в определенный момент времени. Совокупность векторов, изображающих синусоидальные величины одинаковой частоты, называют векторной диаграммой.
Так как на векторной диаграмме представляют переменные величины одной частоты, то вращение векторов происходит с одной и той же угловой скоростью, а, следовательно, взаимное расположение их во времени остается неизменным. Это дает возможность наглядно видеть взаимное расположение синусоидальных величин в пространстве.
Построение векторных диаграмм существенно упрощает анализ цепей переменного тока. В большинстве случаев диаграммы используют лишь для того, чтобы, руководствуясь показываемыми ими соотношениями, составить уравнения Кирхгофа. В таких случаях нет необходимости строить диаграммы в точно определенных масштабах.
На векторных диаграммах взаимное расположение векторов не зависит от выбранного момента времени и направления первого вектора.
Дата добавления: 2015-06-17; просмотров: 963;
