Поперечні коливання струни з вантажами

Розглянемо закріплену на кінцях струну з N вантажами, кожен маси M. Відстань між вантажами – 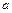, натяг «пружин» в рівновазі одно 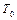(рис. 7.2). Сила натягу 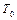передбачається значною, щоб можна було знехтувати дією сили тяжіння.

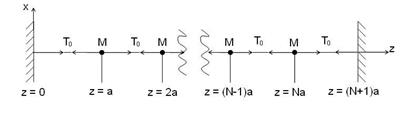
Рисунок 7.2 – Упорядкована лінійна структура пов'язаних вантажів

Обмежимося розглядом тільки поперечних коливань вантажів вздовж осі Х; зміщення позначимо через .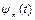

Знайдемо рівняння руху «n» вантажу. (Схема конфігурації струни представлена на рис. 7.3). Враховуючи наближення малих коливань, закон Ньютона дає наступне рівняння руху:

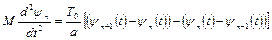. (7.1)

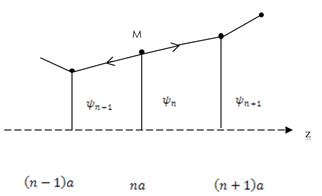
Рисунок 7.3 – Схема конфігурації струни в деякий момент часу

Визначимо частоти і конфігурації окремих мод. Припустимо, що ми маємо моду з частотою . Кожен вантаж здійснює гармонійні коливання з частотою і фазою 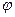, а форма моди визначається відношенням амплітуд коливань різних вантажів. Позначимо через 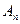- амплітуду коливання n-го вантажу для даної моди. Тоді має

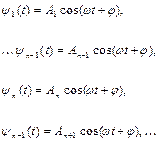(7.2)

З (7.2) знаходимо

(7.3)

Підставляючи (7.3) і (7.2) в рівняння (7.1) отримуємо

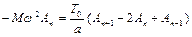
або

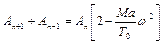. (7.4)

Рівняння (7.4) визначає залежність форми коливання від частоти. Спробуємо знайти рішення (7.4) у вигляді

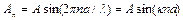, (7.5)

де .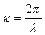

Тоді

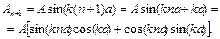
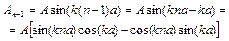
і, отже,

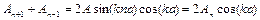. (7.6)

Підставляємо (7.6) в (7.4), одержимо

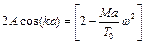. (7.7)

Припускаємо, що (7.7) справедливо для будь-якого вантажу n, незалежно від того чи перебуває він чи ні в вузловій точці, тобто приймаємо 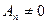. Отже, щоб 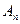було рішенням рівняння (7.4), потрібно виконання умови

,

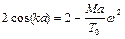звідки

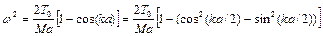
або

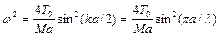. (7.8)

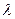Вираз (7.8), що зв'язує частоту і «довжину хвилі» (див. курс математичної фізики), або хвильове число k для даної моди, називається дисперсійним співвідношенням для струни з вантажами.

На рис.7.4 показаний графік і 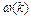для струни з п'ятьма вантажами, закріпленої з обох кінців.