Затухающие колебания. Все реальные колебательные системы являются диссипативными

Все реальные колебательные системы являются диссипативными. Энергия механических колебаний такой системы постепенно расходуется на работу против сил трения, поэтому свободные колебания затухают – их амплитуда постепенно уменьшается.

При небольших скоростях движения силы, вызывающее затухание колебаний, пропорциональны величине скорости 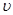. Эти силы называют силами сопротивления (трения):

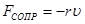, (8)

где 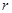- коэффициент сопротивления.

Знак минус указывает, что сила сопротивления всегда направлена в сторону, противоположную направлению движения.

Запишем второй закон Ньютона для затухающих прямолинейных колебаний тела:

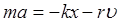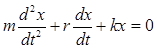или (9)

Решив это дифференциальное уравнение, получим уравнение затухающих колебаний материальной точки:

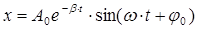, (10)

где 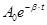- амплитуда затухающего колебания;

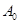- амплитуда в начальный момент времени ( 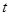=0);

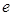- основание натуральных логарифмов;

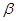- коэффициент затухания, связанный с коэффициентом сопротивления 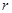и массой 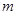соотношением:

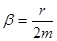(11)

Скорость затухания колебаний оценивается величиной 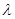, которая называется логарифмическим декрементом затухания.

Логарифмический декремент затухания 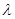равен натуральному логарифму отношения амплитуд колебаний, следующих друг за другом через промежуток времени, равный периоду Т:

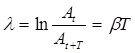(12)

Выясним физический смысл величин 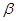и 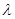. Пусть за время 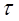амплитуда колебаний уменьшается в 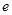раз. Тогда 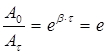, отсюда 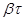= 1 или .

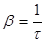Следовательно, коэффициент затухания 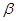есть физическая величина, обратная промежутку времени 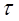, в течение которого амплитуда уменьшается в 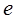раз.

Пусть N – число колебаний, после которых амплитуда уменьшается в 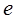раз.

Тогда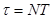

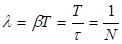
Следовательно,логарифмический декремент затухания 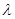есть физическая величина, обратная числу колебаний 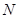, по истечении которых амплитуда уменьшается в 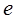раз.