Стоячие волны. Важным случаем интерференции волн является сложение двух когерентных волн, движущихся навстречу друг другу вдоль одной прямой

Важным случаем интерференции волн является сложение двух когерентных волн, движущихся навстречу друг другу вдоль одной прямой. При наложении этих волн возникает стоячая волна – периодическое во времени синфазное колебание с характерным пространственным распределением амплитуды – чередованием узлов и пучностей.

Стоячая волна может быть получена, если прямая волна, посланная вибратором к препятствию, наложится на отраженную от него волну. Уравнение стоячей волны получим сложением уравнения прямой волны

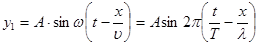
и уравнения отраженной волны, движущейся в направлении противоположном прямой волне

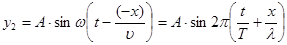
Смещение точки, участвующей одновременно в двух колебаниях, равно:

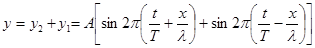
Из тригонометрии известно, что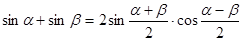

Поэтому окончательно получим уравнение стоячей волны:

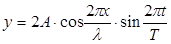, (1)

где 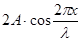= 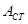- амплитуда стоячей волны, зависит от координаты точки х. Иными словами, амплитуды колебания различных точек различны.

Точки, в которых амплитуда максимальная, называются пучностями (точки 1,3,5).

Точки, в которых амплитуда равна нулю, в колебании не участвуют и называются узлами (точки 2,4,6)

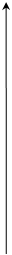
У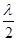

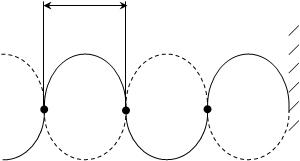1 2 3 4 5 6

Расстояние между соседними узлами (или пучностями) называется длиной стоячей волны:

,

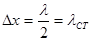где 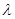- длина бегущих волн.

В отличие от бегущей волны в стоячей волне не происходит переноса энергии, а осуществляется лишь пространственная перекачка энергии одного вида в энергию другого вида.