Теория метода и описание установки

Для выполнения работы необходимо предварительно изучить тему “Механические колебания “.

В данной работе рассматриваются собственные незатухающие колебания простейшей колебательной системы - пружинного маятника. Он представляет собой груз массой m , подвешенный на упругой пружине. Будем считать, что масса пружины мала по сравнению с массой груза.

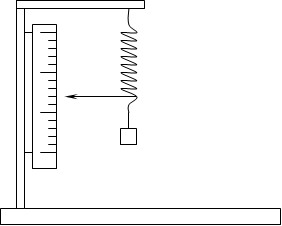
Лабораторная установка состоит из штатива со шкалой. К штативу прикреплена пружина с подвешенным к ней грузом в форме полого медного цилиндра. Масса цилиндра указана на установке. Амплитуда колебаний маятника измеряется по вертикальной шкале.

При подвешивании к пружине груза массой 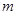она удлинится на величину 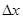, называемую статическим удлинением пружины. Когда маятник находится в состоянии равновесия, сила тяжести уравновешивается силой упругости пружины:

mg = - k 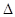x.

Отсюда коэффициент упругости 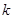равен:

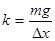(1)

Если пружинный маятник вывести из состояния равновесия, слегка оттянув пружину вниз, то он будет совершать собственные колебания под действием упругой силы

F = -kx , (2)

где k - коэффициент упругости;

x - смещение.

Эта сила сообщает маятнику ускорение и равна

F = ma , (3)

где a - ускорение;

m - масса маятника.

Уравнение собственных колебаний маятника запишется в виде:

-kx = ma (4)

Ускорение a = - w² x , где 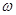- циклическая частота.

Подставив это выражение в уравнение (4), получим:

-kx = - mw² x

или k = mw² (5).

Циклическую частоту w выразим через период Т колебаний и, подставив в (5), найдем период колебаний пружинного маятника:

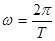
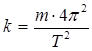, отсюда 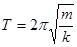(6)

Период колебаний пружинного маятника не зависит от амплитуды колебаний, а зависит от массы и коэффициента упругости пружины.