Краткая теория

Колебательным движениемназывается всякое движение или изменение состояния, характеризуемое той или иной степенью повторяемости во времени значений физических величин, определяющих это движение или состояние. Колебания свойственны всем явлениям природы: пульсирует излучение звезд; с высокой степенью периодичности вращаются планеты Солнечной системы; ветры возбуждают колебания и волны на поверхности воды; внутри любого живого организма непрерывно происходят разнообразные, ритмично повторяющиеся процессы, например, с удивительной надежностью бьется человеческое сердце.

В физике выделяются колебания механическиеи электромагнитные. С помощью распространяющихся механических колебаний плотности и давления воздуха, воспринимаемых нами как звук, а также очень быстрых колебаний электрических и магнитных полей, воспринимаемых нами как свет, мы получаем большое число прямой информации об окружающем мире. Примерами колебательного движения в механике могут быть колебания маятников, струн, мостов и т.д.

Колебания называются периодическими, если значения физических величин, изменяющихся в процессе колебаний, повторяются через равные промежутки времени. Простейшим типом периодических колебаний являются гармонические колебания. Гармоническими называются колебания, при которых изменение колеблющейся величины со временем происходит по закону синуса (или косинуса):

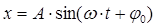, (1)

где x – смещение от положение равновесия;

А – амплитуда колебания – максимальное смещение от положения равновесия;

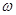- циклическая частота;

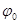- начальная фаза колебания;

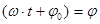- фаза колебания; она определяет смещение в любой момент времени, т.е. определяет состояние колебательной системы.

В случае строго гармонических колебаний величины А, 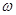и 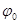не зависят от времени.

Циклическая частота 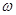связана с периодом Т колебаний и частотой 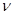соотношением:

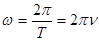(2)

Периодом Тколебаний называется наименьший промежуток времени, по истечении которого повторяются значения всех физических величин, характеризующих колебания.

Частотой 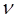колебаний называется число полных колебаний, совершаемых за единицу времени, измеряется в герцах ( 1 Гц = 1 ).

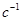Циклическая частота 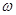численно равна числу колебаний, совершаемых за 2 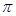секунд.

Колебания, возникающее в системе, не подверженной действию переменных внешних сил, в результате какого-либо начального отклонения этой системы от состояния устойчивого равновесия, называются свободными(или собственными).

Если система консервативная, то при колебаниях не происходит рассеяния энергии. В этом случае свободные колебания называются незатухающими.

Скорость 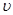колебания точки определим как производную от смещения по времени:

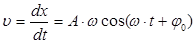(3)

Ускорение 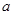колеблющейся точки равно производной от скорости по времени:

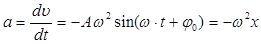(4)

Уравнение (4) показывает, что ускорение при гармонических колебаниях – переменно, следовательно, колебание обусловлено действием переменной силы.

Второй закон Ньютона позволяет в общем виде записать связь между силой F и ускорением 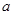при прямолинейных гармонических колебаниях материальной точки с массой :

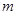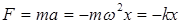, (5)

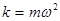где , (6)

к – коэффициент упругости.

Таким образом, сила, вызывающая гармонические колебания, пропорциональна смещению и направлена против смещения. В связи с этим можно дать динамическое определение гармонического колебания: гармоническим называется колебание, вызываемое силой, прямо пропорциональной смещению х и направленной против смещения.

Возвращающей силой может быть, например, сила упругости. Силы, имеющие иную природу, чем упругие силы, но также удовлетворяющие условию (5), называются квазиупругими.

В случае прямолинейных колебаний вдоль оси х ускорение 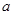равно:

.

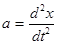Подставив это выражение для ускорения 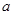и значение силы 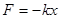во второй закон Ньютона, получим основное уравнение прямолинейных гармонических колебиний:

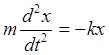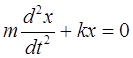или (7)

Решением этого уравнения является уравнение (1).