Основы теории дисперсии

Плодотворная попытка истолкования богатого материала, полученного экспериментальным путем, была сделана еще в «упругой» теории света. Хотя эта теория не могла связать значение показателя преломления среды ни с каким из известных параметров последней, тем не менее истолкование явлений рефракции и дисперсии в веществе предпринято было уже давно.

Согласно представлениям Френеля свет распространяется в особой среде, светоносном эфире, обладающем свойствами упругого твердого тела, крайне разреженного и проникающего во все обычные среды. Скорость световой волны определяется в основном свойствами эфира, но в вещественных средах молекулы изменяют свойства эфира, в них заключенного, и, таким образом, влияют на скорость распространения света. Развивая идею Френеля об учете влияния молекул вещества на частички эфира, Коши (1829—1885 гг.) пришел к формуле, выражающей зависимость показателя преломления от длины волны

n=a + b/ λ₀² + с/ λ₀⁴ +… (2.1)

где λ₀ — длина волны в вакууме, а, b, с, ... — постоянные, значения которых для каждого вещества должны быть определены на опыте. В большинстве случаев можно ограничиться двумя первыми членами формулы (2.1). Формула Коши хорошо передает нормальный ход дисперсии. Так, очень тщательные измерения показателя преломления водорода можно при помощи соответственно подобранных коэффициентов а, b, и с передать формулой Коши очень хорошо.

Теория Коши была создана задолго до открытия аномальной дисперсии. Ее историческое значение очень велико, ибо это была первая работа, показавшая, что волновая теория в состоянии объяснить дисперсию света,

После открытия аномальной дисперсии и установления ее связи с абсорбцией Зельмейер (1871 г.) дал полную теорию явления, основываясь на представлении о взаимодействии молекул весомой среды и эфира. Особенностью теории Зельмейера явилось допущение, что молекулы обладают собственными частотами колебаний, характерными для данного вещества, благодаря чему получило объяснение наличие определенных полос (линий) поглощения. Из рассуждений Зельмейера вытекало, что наличие таких собственных периодов приводит к зависимости показателя преломления от частоты, весьма хорошо передающей весь ход дисперсии как вблизи, так и вдали от полос поглощения. Основы теории Зельмейера сохранились и в дальнейших теориях дисперсии, в том числе и в современной электронной теории. Очень точные измерения зависимости п от λ, выполненные значительно позже (1912 г.) Д. С. Рождественским для паров натрия, показали, что расхождение между теорией Зельмейера и опытом не превышает 2—3%. При этом удалось осуществить измерения вплоть до областей, отличающихся не более чем на 0,5 Å от длины волны, соответствующей собственным колебаниям атома.

В теории Зельмейера оказалось возможным связать оптическую константу (скорость света в веществе) с другими параметрами вещества, с собственными периодами колебаний его молекул, определение которых, правда, должно было выполняться также оптическими методами. Электронное истолкование дисперсии с использованием понятия собственных колебаний атомов установило природу колеблющихся частиц (электроны и ноны) и позволило значительно углубить наши представления о веществе и свете.

В настоящее время в связи с радикальным изменением наших представлений о законах, управляющих поведением атомов и молекул, — изменением, внесенным квантовой теорией, — мы вынуждены пересмотреть и теорию дисперсии. Однако, несмотря на коренную переработку этих представлений, основные существенные черты теории дисперсии сохранились и в квантовой ее трактовке. При этом, однако, не только изменилась точка зрения на явление дисперсии, но и были открыты новые стороны его, не предусмотренные простейшими вариантами классической теории и нашедшие себе в дальнейшем опытное подтверждение (отрицательная абсорбция, некогерентное рассеяние света).

Познакомимся несколько детальнее с основами электронной теории дисперсии. Как уже отмечалось, сущность взаимодействия света и вещества сводится к интерференции падающей (первичной) волны со вторичными волнами, возникающими вследствие колебаний электронов (и ионов) вещества, обусловленных действием поля первичной волны.

В настоящем разделе мы рассмотрим задачу более формально, исследуя зависимость диэлектрической проницаемости среды от частоты световых волн, вызывающих смещение электрических зарядов вещества. Как показывают опыты, главную роль в оптической жизни атома играет электрон; поэтому в дальнейшем мы для удобства будем говорить именно об электроне; однако все наши рассуждения остаются в силе и для иных заряженных частиц, входящих в состав атома. В частности, при исследовании показателя преломления в области длинных волн необходимо учитывать влияние ионов, способных к сравнительно медленным (инфракрасным) колебаниям.

Итак, для вывода зависимости показателя преломления от длины волны найдем, как зависит диэлектрическая проницаемость от частоты переменного электрического поля, и затем перейдем к показателю преломления п на основании соотношения 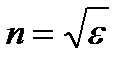. В соответствии с теорией электронов будем рассматривать молекулы или атомы диэлектрика как системы, в состав которых входят электроны, находящиеся внутри молекул в положении равновесия. Под влиянием внешнего поля эти заряды смещаются из положения равновесия на расстояние r, превращая таким образом атом в электрическую систему с моментом величиной р= rе, направленным вдоль поля (диполь). Если в единице объема нашей среды находится N атомов, которые испытывают поляризацию, то электрический момент единицы объема, или поляризация среды, будет равняться Р = Np = Ner. При этом мы для простоты полагали, что в среде имеется лишь один сорт атомов и в каждом из них способен смещаться только один электрон. В противном случае поляризация среды записывалась бы в виде

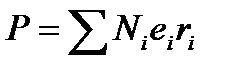
где индекс i относится к i-му сорту зарядов. Зная электрическую поляризацию среды, нетрудно вычислить ее диэлектрическую проницаемость ε, ибо D = ε Е =Е + 4πР, где D - электрическая индукция среды. Итак,

D = ε Е =Е + 4πNer

где r определяется полем Е.

Задача сводится, таким образом, к определению смещения электрона r под действием внешнего, периодически меняющегося поля при учете сил, действующих на электрон, входящий в состав атома, со стороны частей этого атома и окружающих атомов, т. с. представляет собой задачу о вынужденных колебаниях электронов. При этом следует иметь в виду, что речь идет об электронах, частоты движения которых в атоме имеют тот же порядок величины, что и частота световой волны. Только такие электроны испытывают достаточно большое смещение и поэтому участвуют в рассматриваемых здесь процессах. Мы будем их называть оптическими электронами.

а. Силы, действующие на электроны. 1) Удерживающая сила. Чтобы составить представление о характере сил, удерживающих оптический электрон около положения равновесия, надо обратиться к изучению оптических свойств атома. Опыт показывает, что изолированные атомы всех веществ способны испускать практически монохроматические волны с характерными для каждого вещества частотами. Эти частоты не меняются при нагревании вещества, т. е. при увеличении средней энергии, приходящейся на один атом. Следовательно, сила, удерживающая электрон в положении равновесия, должна иметь характер упругой силы (ее называют поэтому квазиупругой), и зависимость ее от смещения электрона определяется законом

F= - br, (2.1)

где b — соответствующая константа упругой связи. Такой закон для силы осуществлялся бы, например, если бы отрицательный электрон находился в центре шара, равномерно заполненного положительными зарядами, взаимодействующими по закону Кулона.

Исследование показывает, что многие свойства атома удается передать при помощи классических законов, применяемых соответственным образом. В частности, взаимодействие атома со световой волной, ведущее к дисперсии света, можно достаточно хорошо описать, если рассматривать атом как совокупность гармонических осцилляторов соответствующей частоты, т. е. считать, что электрон удерживается в атоме квазиупругой силой -br. Таким образом, уравнение движения электрона (массы т), смещенного из положения равновесия и предоставленного действию этой внутриатомной силы, есть

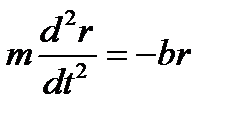
Отсюда

r(t)=r₀cos ω₀t

где r₀ — амплитуда, а 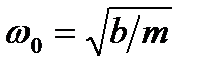— круговая частота собственных колебаний электрона, причем ω₀ зависит от природы атома, определяющей величину константы b. Представление удерживающей силы в виде квазиупругой справедливо, как и в других механических задачах, лишь при достаточно малых отклонениях зарядов от их равновесных положений, т. е. при достаточно малых значениях r. Величина смещения r определяется силой, действующей на оптический электрон со стороны электрического поля, и при больших значениях напряженности последнего выражение (2.1) может оказаться неверным. Известно, например, что как статическое, так и переменное электромагнитное поле может «оторвать» электрон от атома (ионизация), и в этом предельном случае неприменимость соотношения (2.1) вполне очевидна.

Отличие удерживающей силы от квазиупругой фактически оказывается существенным для очень мощного света, который можно получить с помощью оптических квантовых генераторов; это отличие обусловливает особенности так называемых нелинейных оптических явлений. В тех же явлениях, с которыми мы имели дело до сих пор, и во многих других соотношение (2.1) выполняется с очень хорошим приближением.

2) Тормозящая сила. Предположение о гармоническом колебании электрона в атоме имеет лишь приближенный характер. В действительности же электрон, приведенный в колебание, постепенно отдает свою энергию, и, следовательно, амплитуда колебания с течением времени уменьшается. Таким образом, колебание не имеет строго гармонического характера и должно рассматриваться как затухающее. Даже в случае изолированного атома будут совершаться затухающие колебания, ибо энергия будет постепенно покидать атом, излучаясь во все стороны. Кроме такого затухания, неизбежно связанного с излучением, могут иметь место и другие причины растраты колебательной энергии, связанные с взаимодействием атомов между собой, причем в этих случаях энергия колебания может переходить и в другие формы, например в тепло, увеличивая среднюю кинетическую энергию атомов среды.

Мы вернемся ниже к обсуждению различных физических причин, обусловливающих затухание колебаний в атоме. Во всяком случае, все они ведут к уменьшению амплитуды колебания и, следовательно, влияют на движение электрона как некая тормозящая (диссипативная) сила. Сила эта, как показывает опыт, во многих случаях сравнительно мало искажает собственные колебания атома, так что растраченная за один период энергия составляет лишь ничтожную часть (порядка одной стомиллионной) колебательной энергии атома. При таких условиях можно учесть эту силу, положив ее пропорциональной скорости движения электрона 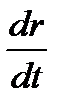, подобно тому как во многих задачах механики сила трения может считаться пропорциональной скорости движения частицы. Исследование различных физических причин затухания показывает, что они согласуются с подобным выражением для тормозящей силы. Итак, в качестве второй силы, действующей на электрон, мы вводим силу сопротивления, или торможения

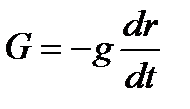
где коэффициент g зависит от природы среды.

3) Вынуждающая сила. Вынужденные колебания электрона возникают под действием световой волны, распространяющейся в среде. Магнитная составляющая этого поля оказывает лишь малое действие, ибо магнитное поле действует только на движущийся заряд. Поэтому во всех практических задачах можно ограничиться учетом действия лишь электрического ноля волны. Мы принимаем, таким образом, что действие световой волны определяется напряженностью электрического поля, т. е. на электрон действует сила еЕ, где Е = Е₀ соs ωt — поле волны. Это справедливо только тогда, когда можно пренебречь действием окружающих молекул, также поляризованных приходящей световой волной. Такое допущение справедливо для разреженных газов, где расстояние между молекулами среды велико. Для газов, находящихся под значительным давлением, для жидкостей или твердых тел необходимо учитывать это влияние, что поведет к изменению выражения для силы, действующей на электрон.

б. Уравнение дисперсии. Сделав вышеуказанные допущения относительно действующих сил, мы можем написать для электрона ньютоново уравнение движения

(2.2)

которое представляет собой уравнение движения при вынужденных колебаниях. Решив это уравнение, определим r, а, следовательно, и Р == Np = Ner, и найдем таким образом ε = n² в зависимости от констант атома (е, т, ω₀, g) и частоты со внешнего поля, т. е. решим задачу дисперсии. Решение уравнения (2.2) не представляет затруднений, хотя несколько длинно. Основные особенности движения электронов под действием вынуждающей силы нетрудно получить значительно проще, если предположить, что силой сопротивления можно пренебречь, т. е. что g = 0. Поле световой волны Е можно считать простой синусоидальной функцией частоты ω, т. е. Е = Е₀sin ωt, ибо по теореме Фурье поле иного вида всегда можно представить в виде суперпозиции таких функций, и решение более общей задачи сводится к решениям более простых задач такого типа. Положив g= 0 и разделив обе части уравнения (2.2) на т, придадим ему вид

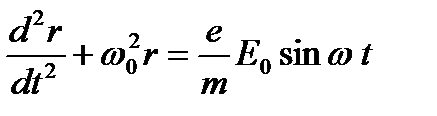(2.3)

где 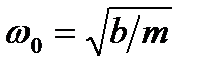— частота собственного колебания электрона. Решение уравнения (2.3) можно записать следующим образом:

r=Asin ωt

где 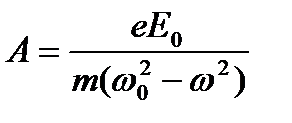, в чем легко убедиться подстановкой. Определив r, найдем

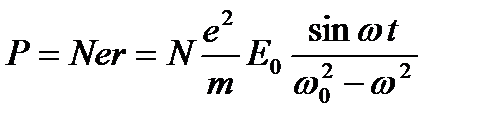
и отсюда на основании соотношения D=εE=E+4πР как окончательное решение нашей упрощенной задачи получим

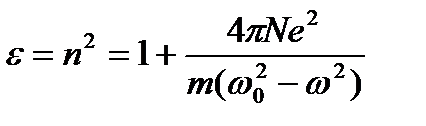(2.4)

Согласно этой формуле показатель преломления зависит от частоты ω внешнего поля, т. е. найденная формула передает явление дисперсии света, правда, при несколько упрощенных допущениях, которые в дальнейшем надо устранить.

Как видно из (2.4), в области от ω = 0 до ω = ω₀ показатель преломления п больше единицы и возрастает при возрастании ω (нормальная дисперсия); при ω = ω₀ имеем п² = ± 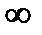; в области от ω = ω₀ до ω = 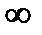п² меньше единицы и также возрастает от — 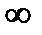до 1 (нормальная дисперсия).

Обращение показателя преломления в бесконечность не имеет физического, смысла и получилось в результате упрощенного предположения об отсутствии сопротивления движению (g=0), обусловливающего затухание. Если принять это сопротивление в расчет, то ход кривой будет иным (рис. 2.1, сплошная кривая). Область МN — область аномальной дисперсии, где п убывает при возрастании частоты ω.

Формулу (2.4) можно преобразовать. Перенеся 1 в левую часть, запишем ее в виде n² — 1 = (п + 1) (п — 1). Поскольку п обычно не очень сильно отличается от единицы, множитель (n — 1), вообще говоря, изменяется в зависимости от п значительно сильнее, чем (п + 1). Опыт показывает, что величину (п — 1) можно с хорошим приближением считать пропорциональной плотности вещества. Следовательно, N в формуле (2.4) также допустимо считать пропорциональным плотности или числу атомов N₀ в единице объема. Итак, положим N=fN₀; безразмерный коэффициент f обычно называют силой осциллятора, желая подчеркнуть долю участия этих осцилляторов пли их эффективность в явлениях дисперсии. Таким образом, формула (2.4) принимает вид

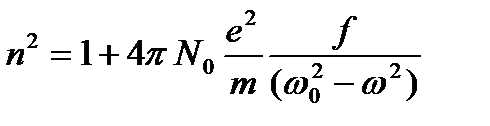(2.5)

Если принять во внимание, что в веществе может быть несколько сортов зарядов, способных к колебаниям с различными собственными частотами ω_0i и, может быть, с различными зарядами е_i, и массами т_i, то формула (2.5) заменится выражением

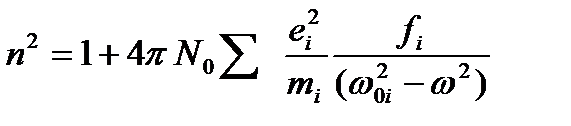(2.6)

где f_i — силы, или эффективности, отдельных сортов осцилляторов, соответствующих различным частотам ω_0i.

В таком случае дисперсионная кривая распадается на ряд ветвей, причем в отсутствие затухания значения n², соответствующие каждому ω = ω_0i, равны ±оо. Если учесть затухание, то кривая будет иметь вид, показанный на рис. 2.2.

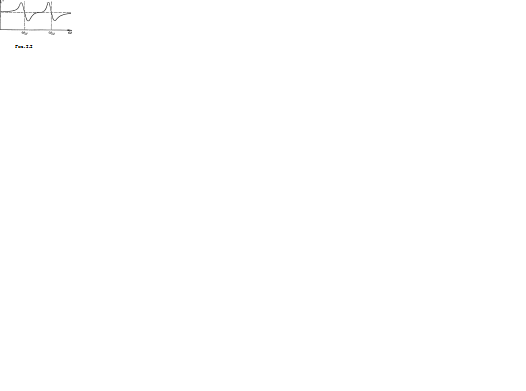Нетрудно видеть, что наибольший вклад в (2.6) вносят именно оптические электроны, для которых частоты ω_0i примерно такие же, как и частоты видимого света ω. Те члены суммы, для которых ω_0i значительно превышают ω, малы.

Зная по ходу дисперсионной кривой значения п вблизи разных ω_0i можно оценить какие заряды е_i и массы m_i фигурируют в нашей формуле, т. е. определить, какие электрические элементы атома участвуют в явлении дисперсии. Однако точное определение отношения е_i/m_i невозможно, поскольку остаются неопределенными величины f_i. Правда, если сделать несколько произвольное предположение, что f_i имея для разных осцилляторов различные значения, меняется не в тысячи раз, а значительно меньше, то можно прийти к весьма важным выводам. Окажется, что зна­чения е_i/m_i распадаются на две большие группы: в области высоких частот (видимая и ультрафиолет) величины е_i/m_i соответствуют данным для электронов, а в области низких частот (инфракрасное излучение) оно в тысячу раз меньше и соответствует скорее ионам вещества. Ряд физических эффектов (явление Зеемана, например) с несомненностью показало, что с испусканием видимого и ультрафиолетового света связаны колебания электронов. В таком случае предыдущее замечание, несмотря на известную произвольность допущения относительно f_i приобретает глубокий смысл и перестает казаться случайным совпадением: некоторые осцилляторы, несомненно, представляют колебания электронов. Естественно поэтому признать, что другие осцилляторы низкой частоты, играющие роль в инфракрасной части спектра, представляют колебания заряженных ионов вещества.

Считая, таким образом, значения е_i/m_i установленными для разных осцилляторов, можно из формулы (2.6) определить силы осцилляторов. Такие оценки показывают, что и для осцилляторов электронного типа значения f_i могут быть довольно различными, т. е. не все электронные осцилляторы участвуют в явлении дисперсии с одинаковой эффективностью.