Энергия, переносимая упругими волнами

5.7.1 Энергия волны

Как было сказано выше, основным свойством бегущих волн является перенос энергии без переноса вещества. Вместе с тем, каждая единица объема упругой среды при прохождении волны обладает энергией. Эта энергия скла-дывается из кинетической энергии 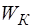движущихся час-тиц среды и потенциальной энергии 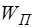упругой дефор-мации среды:

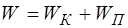. (5.139)

Для получения выражения, описывающего энергию вол-ны, рассмотрим малый объем dV стержня, через который распространяется плоская волна. Скорости частиц среды в этом объеме одинаковы и равны

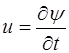, (5.140)

относительная деформация среды:

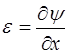. (5.141)

Рассмотриваемый объем обладает массой:

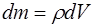, (5.142)

где 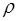– плотность среды. Тогда кинетическая энергия, которой обладает рассматриваемый объем при прохожде-нии волны, определяется как:

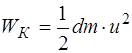. (5.143)

Получим выражение для потенциальной энергии. Для этого выделим в среде участок длиной l и площадью по-перечного сечения S (рис. 5.13). При прохождении волны рассматриваемый участок попеременно испытывает сжа-тия и растяжения. Рассмотрим случай, когда участок рас-тягивается. При этом его длина получает приращение Δl, а объем V – приращение ΔV за счет действующей на рас-сматриваемый участок силы .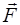

Потенциальная энергия упругого растяжения опреде-лится как:

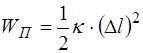, (5.144)

где 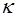– коэффициент упругости среды. Найдем его. Си-ла, растягивающая рассматриваемый участок, связана с величиной растяжения 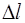(в проекции на ось X):

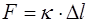, (5.145)

и эта сила создает нормальное напряжение:

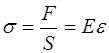, (5.146)

где 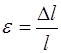– относительная деформация рассматриваемого участка.

Таким образом,

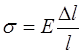, (5.147)

что позволяет записать следующее выражение для силы:

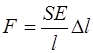. (5.148)

Из определения упругой силы (5.145) найдем коэффи-циент жесткости:

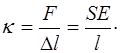(5.149)

Подставив полученное выражение в уравнение для по-тенциальной энергии (5.144), получим:

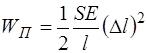. (5.150)

Учтя, что 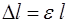, получим:

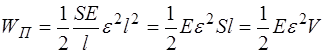. (5.151)

Перейдя к бесконечно малому объему, получим окон-чательно:

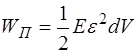. (5.152)

Таким образом, при прохождении волны среда облада-ет дополнительной энергией:

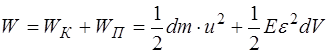. (5.153)

5.7.2 Энергия гармонической волны

Рассмотрим гармоническую волну, распространяющу-юся в положительном направлении оси X:

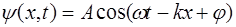. (5.154)

Скорость движения частиц среды при прохождении волны определится как:

, (5.155)

а относительная деформация среды

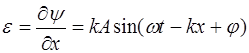. (5.156)

Подставляя уравнения для скорости (5.155) и отно-сительной деформации (5.156) в выражение для энергии волны (5.153), получим:

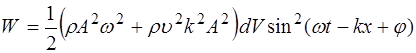(5.157)

Здесь было учтено, что модуль Юнга, исходя из (5.115) может быть выражен через плотность среды и скорость распространения волны ( 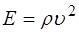). Кроме того, исходя из определения волнового числа (5.7), сделаем замену 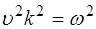. Получим закон изменения энергии, сообщае-мой волной при прохождении объема dV:

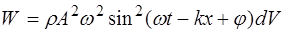. (5.158)

Разделив на объем dV, получим плотность энергии волны:

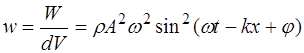. (5.159)

Найдем среднее значение плотности энергии в данной точке за период колебаний. Поскольку плотность энергии зависит от квадрата синуса, найдем среднее значение квадрата синуса за период:

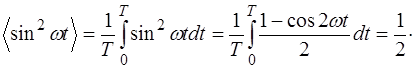(5.160)

Таким образом, среднее значение плотности энергии в данной точке за период (или промежуток времени, значи-тельно превышающий период), будет равно:

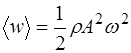. (5.161)

5.7.3 Плотность потока энергии

Среда, в которой распространяются волны, обладает ме-ханической энергией, которая переносится от источника колебаний в различные точки пространства самой вол-ной. Количество энергии, переносимое волной через по-верхность площадью 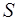за единицу времени, называется потоком энергии через эту поверхность:

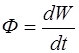, (5.162)

где 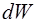– энергия, переносимая через поверхность за вре-мя .

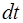Поток энергии – скалярная величина, ее размерность совпадает с размерностью мощности. Поэтому поток энергии измеряется в ваттах:

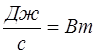. (5.163)

Поскольку поток энергии в разных точках поверхности 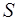может иметь различную интенсивность, то для харак-теристики интенсивности вводят понятие плотности по-тока энергии.

Рассмотрим волну, переносящую энергию со скоростью 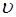через элементарную площадку 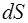, расположенную под углом 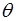к направлению распространения волны (рис. 5.14).

За время dt через площадку dS пройдет энергия dW, содержащаяся в косом цилиндре, имеющего основание площадью 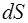и образующей с длиной 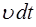, где 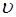– ско-рость переноса энергии (возмущения). Размеры этого ци-линдра должны быть настолько малы, чтобы во всех его точках плотность энергии была одинакова. Тогда прошед-шая энергия:

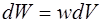, (5.164)

где 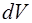– объем цилиндра;

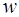– плотность энергии.

Следовательно, энергия, заключенной в цилиндре:

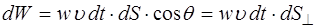, (5.165)

где 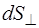– площадка, перпендикулярная направлению переноса энергии (направлению распространения волны).

С учетом этого, поток энергии через площадку dS будет равен:

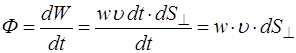. (5.166)

Таким образом, плотность потока энергии – это поток энергии через единичную площадку, перпендикулярную к направлению переноса энергии:

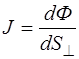, (5.167)

где ;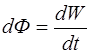

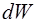– энергия, заключенная внутри косого цилиндра.

С учетом соотношения (5.166) выражение для плот-ности потока энергии примет вид:

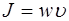(5.168)

Запишем последнее выражение в векторном виде. Для этого введем вектор фазовой скорости 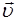, модуль которо-го равен фазовой скорости волны, а направление совпа-дает с направлением распространения волны (и переноса энергии). Тогда мы получим вектор плотности потока энергии, называемый вектором Умова :

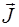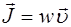, (5.169)

где 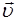– вектор скорости распространения волны, нор-мальный к волновой поверхности в данном месте.

Из (5.29) видно, что для гармонической волны 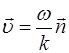. Как и плотность потока энергии, так и вектор Умова различен в разных точках пространства, а в данной точке пространства (в случае гармонической волны) изменяется по закону квадрата синуса. Его среднее значение равно:

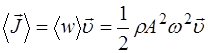. (5.170)

Это выражение справедливо для любого вида волн. Среднее по времени значение плотности потока энергии, переносимой волной, называется интенсивностью волны:

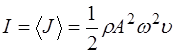. (5.171)

Единица измерения плотности потока и интенсивности:

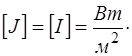(5.172)

Зная закон изменения вектора Умова 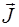во всех точках интересующей нас поверхности 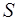, можно найти поток энергии через эту поверхность. Мысленно разобьем поверхность 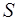на элементарные участки 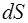. Поток энер-гии через этот участок 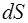есть:

, (5.173)

где 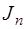– проекция вектора 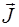на нормаль 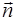к поверх-ности 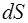. Тогда полный поток сквозь поверхность 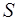рассчитаем как интеграл по всей поверхности :

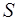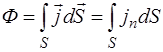. (5.174)

Здесь .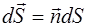

Выражение (5.174) означает, что поток энергии сквозь поверхность 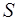равен потоку вектора 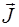сквозь эту повер-хность 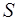. Среднее значение потока энергии можно рас-считать, заменив в выражении вектор 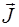его средним зна-чением:

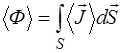. (5.175)

В качестве примера найдем зависимость амплитуды незатухающей сферической волны от растояния 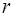до источника. Для этого найдем среднее значение 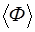потока энергии через одну из ее волновых поверхностей. В каждой точке этой поверхности векторы 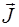и 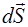сов-падают по направлению. Кроме того, модуль вектора Умова 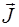для всех точек волновой поверхности одинаков. Следовательно,

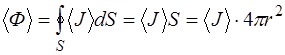, (5.176)

где 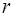– радиус волновой поверхности.

Подставляя в (5.176) выражение (5.171), получим сред-нее значение потока через волновую поверхность радиуса :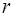

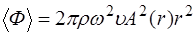. (5.177)

Здесь 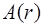– амплитуда волны на расстоянии 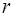от ис-точника. Поскольку энергия волны не поглощается сре-дой, то средний поток через сферу любого радиуса дол-жен быть одним и тем же, то есть должно выполняться условие:

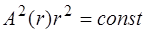. (5.178)

Отсюда следует, что амплитуда незатухающей сфери-ческой волны 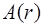обратно пропорциональна расстоянию 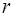от источника:

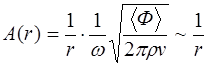, (5.179)

что доказывает справедливость выражения (5.39).