Стоячие волны. 6.1 Стоячие волны в упругой среде

6.1 Стоячие волны в упругой среде

Согласно принципу суперпозиции, при распростране-нии в упругой среде одновременно нескольких волн воз-никает их наложение, причем волны не возмущают друг друга: колебания частиц среды являются векторной сум-мой колебаний, которые совершали бы частицы при рас-пространении каждой из волн в отдельности.

Волны, создающие колебания среды, разности фаз меж-ду которыми в каждой точке пространства постоянны, на-зываются когерентными.

При сложении когерентных волн возникает явление интерференции, заключающееся в том, что в одних точ-ках пространства волны усиливают друг друга, а в других точках – ослабляют. Важный случай интерференции наб-людается при наложении двух встречных плоских волн с одинаковой частотой 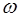и амплитудой 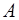. Возникающие при этом колебания называют стоячей волной. Чаще все-го стоячие волны возникают при отражении бегущей вол-ны от преграды. При этом падающая волна и отраженная навстречу ей волна при сложении дают стоячую волну.

Получим уравнение стоячей волны. Возьмем две плос-кие гармонические волны, распространяющиеся навстечу друг другу вдоль оси X и имеющие одинаковую частоту 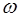и амплитуду :

,

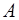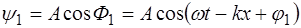(6.1)

,

где 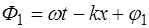– фаза колебаний точек среды при про-хождении первой волны;

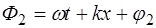– фаза колебаний точек среды при про-хождении второй волны.

Разность фаз в каждой точке на оси X не будет зави-сеть от времени, т.е. будет постоянной:

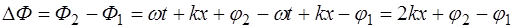(6.2)

Следовательно, обе волны будут когерентными.

Возникшее в результате сложения рассматриваемых волн колебание частиц среды будет следующим:

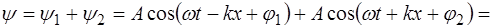
. (6.3)

Преобразуем сумму косинусов углов по правилу (4.4) и получим:

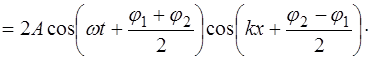(6.4)

Перегруппировав множители, получим:

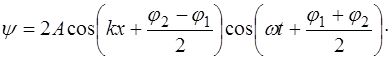(6.5)

Для упрощения выражения выберем начало отсчета так, чтобы разность фаз 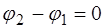и начало отсчета времени 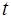, чтобы и сумма фаз была равна нулю: .

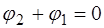Тогда уравнение для суммы волн примет вид:

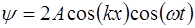. (6.6)

Уравнение (6.6) называется уравнением стоячей вол-ны. Из него видно, что частота стоячей волны 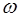равна частоте бегущей волны, а амплитуда, в отличие от бегу-щей волны, зависит от расстояния от начала отсчета :

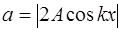. (6.7)

С учетом (6.7) уравнение стоячей волны принимает вид:

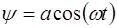. (6.8)

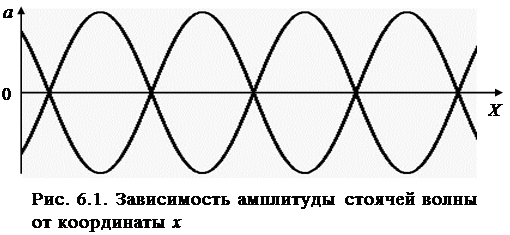
Таким образом, точки среды колеблются с частотой 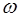, совпадающей с частотой бегущей волны, и амплитудой a, зависящей от положения точки на оси X. Соответственно, амплитуда изменяется по закону косинуса и имеет свои максимумы и минимумы (рис. 6.1).

Для того, чтобы наглядно представить расположение минимумов и максимумов амплитуды заменим, согласно (5.29), волновое число его значением:

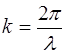. (6.9)

Тогда выражение (6.7) для амплитуды примет вид

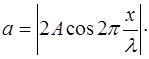(6.10)

Отсюда становится видно, что амплитуда смещения мак-симальна при 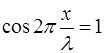, т.е. в точках, координата кото-рых удовлетворяет условию:

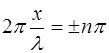, (6.11)

где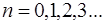

Отсюда получаем координаты точек, где амплитуда сме-щения максимальна:

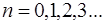; (6.12)

Точки, где амплитуда колебаний среды максимальна, называются пучностями волны.

Амплитуда волны равна нулю в точках, где 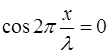. Координата таких точек, называемых узлами волны, удов-летворяет условию:

, (6.13)

где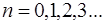

Из (6.13) видно, что координаты узлов имеют зна-чения:

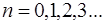, (6.14)

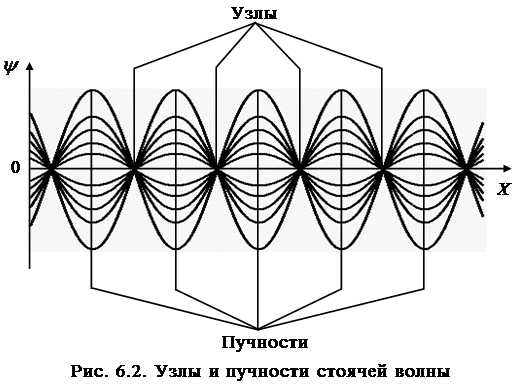
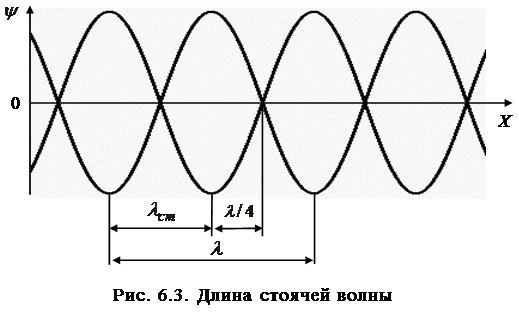
На рис. 6.2 показан примерный вид стоячей волны, от-мечено расположение узлов и пучностей. Видно, что со-седние узлы и пучности смещения отстоят друг от друга на одно и то же расстояние.

Найдем расстояние между соседними пучностями и уз-лами. Из (6.12) получаем расстояние между пучностями:

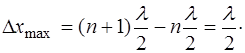(6.15)

Расстояние между узлами получаем из (6.14):

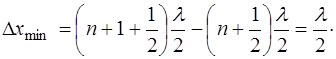(6.16)

Из полученных соотношений (6.15) и (6.16) видно, что расстояние между соседними узлами, как и между сосед-ними пучностями, постоянно и равно 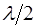; узлы и пуч-ности сдвинуты относительно друг друга на 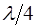(рис. 6.3).

Из определения длины волны можно записать выра-жение для длины стоячей волны: она равна половине дли-ны бегущей волны:

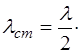(6.17)

Запишем, с учетом (6.17), выражения для координат уз-лов и пучностей:

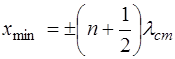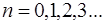, (6.18)

, (6.19)

Множитель 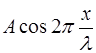, определяющий амплитуду стоя-чей волны, меняет свой знак при переходе через нулевое значение, вследствие чего фаза колебаний по разные сто-роны от узла отличается на . Следовательно, все точки, лежащие по разные стороны от узла, колеблются в про-тивофазе. Все точки, находящиеся между соседними уз-лами, колеблются синфазно.

Узлы условно разделяют среду на автономные области, в которых гармонические колебания совершаются незави-симо. Никакой передачи движения между областями нет, и, значит, перетекания энергии между областями нет. То есть нет передачи возмущения вдоль оси . Поэтому волна называется стоячей.

Итак, стоячая волна образуется из двух противополож-но направленных бегущих волн равных частот и амп-литуд. Векторы Умова каждой из этих волн равны по мо-дулю и противоположны при направлению, и при сложе-нии дают ноль. Следовательно, стоячая волна энергии не переносит.

6.2 Примеры стоячих волн

6.2.1 Стоячая волна в струне

Расмотрим струну длиной L, закрепленную с обоих кон-цов (рис. 6.4).

Расположим вдоль струны ось X таким образом, чтобы левый конец струны имел координату x=0, а правый – x=L. В струне возникают колебания, описываемые урав-нением:

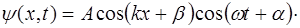(6.20)

Запишем граничные условия для рассматриваемой стру-ны. Поскольку её концы закреплены, то в точках с коор-динатами x=0 и x=L колебаний нет:

(6.21)

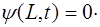(6.22)

Найдем уравнение колебаний струны исходя из запи-санных граничных условий. Запишем уравнение (6.20) для левого конца струны с учетом (6.21):

(6.23)

Соотношение (6.23) выполняется для любого времени t в двух случаях:

1. 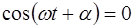. Это возможно в том случае, если коле-бания в струне отсутствуют ( 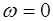). Данный случай инте-реса не представляет, и мы его рассматривать не будем.

2. . Здесь фаза 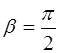. Этот случай и позволит нам получить уравнение колебаний струны.

Подставим полученное значение фазы 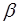в граничное условие (6.22) для правого конца струны:

. (6.25)

Учитывая, что

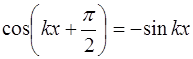, (6.26)

из (6.25) получим:

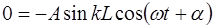. (6.27)

Снова возникают два случая, при которых выполняется соотношение (6.27). Случай, когда колебания в струне от-сутствуют ( 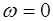), мы рассматривать не будем.

Во втором случае должно выполняться равенство:

, (6.27)

а это возможно, только когда аргумент синуса кратен це-лому числу :

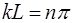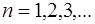, (6.28)

Значение мы отбрасываем, т.к. при этом 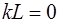, а это означало бы или нулевую длину струны (L=0) или вол-новое число k=0. Учитывая связь (6.9) между волновым числом и длиной волны видно, что для того, чтобы вол-новое число равнялось бы нулю, длина волны должна бы быть бесконечной, а это означало бы отсутствие колебаний.

Из (6.28) видно, что волновое число при колебаниях струны, закрепленной с обоих концов, может принимать только определенные дискретные значения:

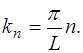(6.30)

Учитывая (6.9), запишем (6.30) в виде:

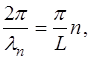(6.31)

откуда волучаем выражение для возможных длин волн в струне:

(6.31)

Другими словами, на длине струны L должно уклады-ваться целое число n полуволн:

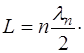(6.32)

Соответствующие частоты колебаний можно опреде-лить из (5.7):

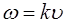. (6.33)

Здесь 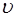– фазовая скорость волны, зависящая, соглас-но (5.102), от линейной плотности струны 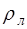и силы на-тяжения струны :

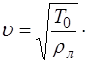(6.34)

Подставив (6.34) в (6.33), получим выражение, описы-вающее возможные частоты колебаний струны:

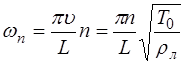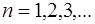, (6.36)

Частоты называют собственными частотами стру-ны. Частоту 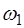(при n = 1):

(6.37)

называют основной частотой (или основным тоном) струны. Частоты, определяемые при n>1 называются обертонами или гармониками. Номер гармоники равен n-1. Например, частота :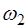

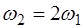(6.38)

соответствует первой гармонике, а частота :

(6.39)

сответствует второй гармонике, и т.д. Поскольку струну можно представить в виде дискретной системы с беско-нечным числом степеней свободы, то каждая гармоника является модой колебаний струны. В общем случае коле-бания струны представляют собой суперпозицию мод.

Каждой гармонике соответствует своя длина волны. Для основного тона (при n=1) длина волны:

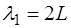, (6.40)

соответственно для первой и второй гармоники (при n=2 и n=3) длины волн будут:

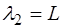, (6.41)

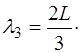(6.42)

На рис.6.5 показан вид нескольких мод колебаний, осуществляемых струной.

Таким образом, струна с закрепленными концами реа-лизует в рамках классической физики исключительный случай – дискретный спектр частоты колебаний (или длин волн). Таким же образом ведет себя упругий стер-жень с одним или обоими зажатыми концами и колебания воздушного столба в трубах, что и будет рассмотрено в последующих разделах.

6.2.2 Влияние начальных условий на движение

непрерывной струны. Фурье-анализ

Колебания струны с зажатыми концами помимо дис-кретного спектра частот колебаний обладают еще одним важным свойством: конкретная форма колебаний струны зависит от способа возбуждения колебаний, т.е. от на-чальных условий. Рассмотрим подробней.

Уравнение (6.20), описывающее одну моду стоячей вол-ны в струне, является частным решением дифференциаль-ного волнового уравнения (5.61). Поскольку колебание стру-ны складывается из всех возможных мод (для струны – бес-конечное количество), то и общее решение волнового уравнения (5.61) складывается из бесконечного числа частных решений:

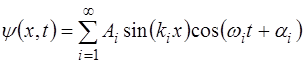, (6.43)

где i – номер моды колебаний. Выражение (6.43) записа-но с учетом того, что концы струны закреплены:

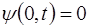, (6.44)

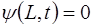, (6.45)

а также с учетом связи частоты i-й моды и ее волнового числа:

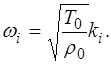(6.46)

Здесь 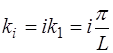– волновое число i-й моды;

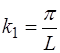– волновое число 1-й моды;

Найдем величину начальной фазы для каждой моды колебаний. Для этого в момент времени t=0 придадим струне форму, описываемую функцией f₀(x), выражение для которой получим из (6.43):

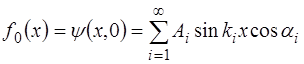. (6.47)

На рис. 6.6 показан пример формы струны, описывае-мой функцией f₀(x).

В момент времени t=0 струна еще покоится, т.е. ско-рость всех ее точек равна нулю. Из (6.43) найдем выраже-ние для скорости точек струны:

, (6.48)

и, подставив в него t=0, получим выражение для скорос-ти точек струны в начальный момент времени:

. (6.49)

Поскольку в начальный момент времени скорость рав-на нулю, то выражение (6.49) будет равно нулю для всех точек струны, если 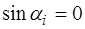. Из этого следует, что на-чальная фаза для всех мод тоже равна нулю ( ). С учетом этого выражение (6.43), описывающее движение струны, принимает вид:

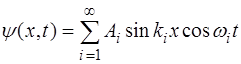, (6.50)

а выражение (6.47), описывающее начальную форму стру-ны, выглядит как:

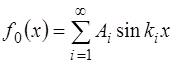. (6.51)

Стоячая волна в струне описывается функцией, перио-дичной на интервал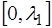е , где 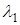равна двум длинам струны (рис. 6.7):

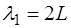. (6.52)

Это видно из того, что периодичность на интервале 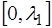означает:

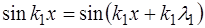. (6.53)

Следовательно,

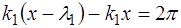; (6.54)

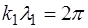; (6.55)

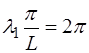, (6.56)

что и приводит нас к выражению (6.52).

Из математического анализа известно, что любая пе-риодическая функция 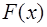может быть разложена с высо-кой точностью в ряд Фурье:

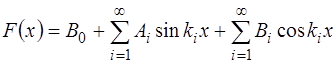, (6.57)

где , , 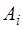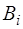– коэффициенты Фурье.

В нашем случае, когда функция является периодичес-кой на интервале 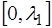, коэффициенты Фурье, согласно [1], рассчитываются как:

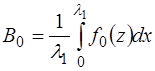, (6.58)

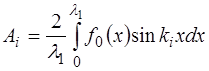, (6.59)

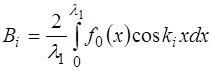, (6.60)

где

. (6.61)

В математике в курсе Фурье-анализа показано, что по-лученные таким образом коэффициенты Фурье для разло-жения периодической функции 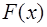фактически и явля-ются коэффициентами разложения функции f₀(x).

Фурье-анализ позволяет разложить колебание, совер-шаемое струной в спектр, т.е. выяснить, какие моды ко-лебаний действительно имеют место при данном способе возбуждения струны.

Рассмотрим два способа возбуждения колебаний струны.

Способ 1. Струне в начальный момент времени прида-ется форма, соответствующая первой моде колебаний и описываемая функцией:

. (6.62)

После того, как струна отпускается, она начинает со-вершать колебания из начального положения. Расчеты по-казывают, что коэффициенты Фурье для этого случая все равны нулю, кроме одного, который равен амплитуде A:

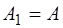. (6.63)

При таком способе возбуждения возникает только одна мода колебаний; никаких обертонов нет.

Способ 2. Струна отводится от положения равновесия посередине, как это происходит в струнных инстру-ментах. Вид начальной формы представлен на рис. 6.8.

Форма струны, изображенная на рис. 6.8, описывается функцией:

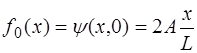при ,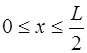

(6.64)

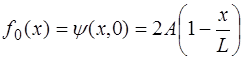при .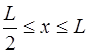

Функция, соответствующая (6.64), и которая является пе-риодической на интервале 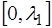, записывается следую-щим образом:

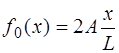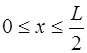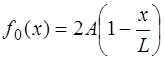при ,

при 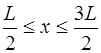, (6.65)

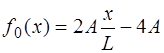при .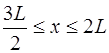

Вид периодической функции (6.65) показан на рис.6.9:

Расчеты показывают, что все коэффициенты Фурье 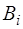для такой функции равны нулю (включая и коэффициент ). Первые три коэффициента A₁, A₂, A₃ соответственно равны:

, (6.66)

, (6.67)

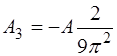. (6.68)

Как уже отмечалось, полученные таким образом коэф-фициенты Фурье для разложения периодической функ-ции 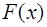фактически и являются коэффициентами разло-жения функции f₀(x).

Тогда, с учетом трех первых слагаемых ряда Фурье, функция (6.64) может быть приближенно представлена следующим образом:

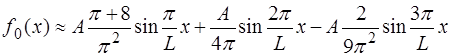(6.69)

Мы нашли только три первых члена Фурье-разложения функции (6.64). Конечно, полученный нами ряд Фурье (6.69) при конечном количестве членов, в нашем случае равном трём, может воспроизвести исходную функцию лишь при-ближённо. Однако, вычисления коэффициентов Фурье могут быть продолжены. Получится, что при рассматриваемом на-ми случае колебаний в струне возникает много гармоник (теоретически, бесконечный ряд гармоник).

Сравнивая первый и второй рассмотренные случаи, мы видим, что в первом из них была только одна мода, а во втором возникает много гармоник.

Таким образом, рассмотренные случаи показывают, что конкретная форма колебаний струны, зажатой с двух сторон, существенно зависит от способа возбуждения ко-лебаний, т.е., от начальных условий.