Скорость волн в упругой среде
5.6.1 Скорость волны в струне
Рассмотрим волну, распространяющуюся в натянутой струне в произвольном направлении. Выделим в струне точку с координатами (x,y,z), находящуюся в равновесии (рис. 5.7). Тогда смещение 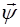 этой точки от положения равновесия при прохождении волны опишется уравне-нием:
этой точки от положения равновесия при прохождении волны опишется уравне-нием:
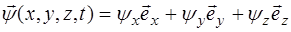 . (5.83)
. (5.83)
Здесь  – проекция смещения
– проекция смещения 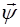 на ось X;
на ось X;
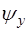 – проекция смещения
– проекция смещения 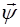 на ось Y;
на ось Y;
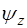 – проекция смещения
– проекция смещения 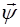 на ось Z;
на ось Z;
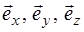 – орты осей
– орты осей 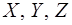 соответственно.
соответственно.
 |
Натянем струну вдоль оси X. В этом случае волна бу-дет распространяться по оси X. Проекции вектора смеще-ния на координатные оси 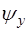 и
и 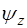 будут описывать попе-речные смещения точек струны от положения равновесия, а
будут описывать попе-речные смещения точек струны от положения равновесия, а  – продольные смещения.
– продольные смещения.
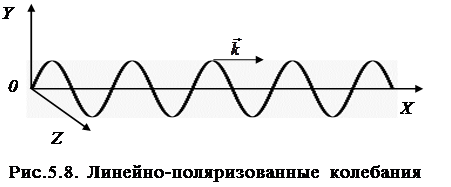 |
Рассмотрим колебания струны, происходящие только вдоль оси Y. Такие колебания называются линейно поля-ризованными вдоль оси Y ( рис.5.8).
При таком виде поляризации частицы имеют смещение относительно положения равновесия только вдоль оси Y, т.е. 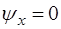 и
и 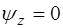 .
.
В этом случае смещение 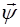 точки, имеющей положение равновесия x опишется уравнением:
точки, имеющей положение равновесия x опишется уравнением:
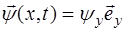 , (5.84)
, (5.84)
а в скалярном виде
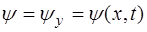 . (5.85)
. (5.85)
Найдем уравнение, описывающее колебания струны, исходя из основного уравнения динамики. Рассмотрим небольшой участок струны длиной dx, начинающийся в точке 1 с координатой x и оканчивающийся в точке 2 с координатой x+dx (рис. 5.9). Участок dx выберем на-столько малым, чтобы силы растяжения T1 и T2, прило-женные к различным концам этого участка, были равны:
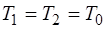 . (5.86)
. (5.86)
Точка 1 имеет смещение  от положения равновесия вдоль оси Y, точка 2 имеет смещение
от положения равновесия вдоль оси Y, точка 2 имеет смещение 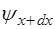 . Рассматрива-емый участок имеет массу:
. Рассматрива-емый участок имеет массу:
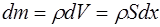 , (5.87)
, (5.87)
где  – плотность материала струны,
– плотность материала струны,
S – площадь поперечного сечения струны.
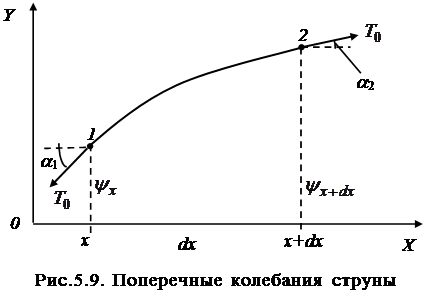
Перейдя к линейной плотности струны, т.е. к массе единицы длины струны:
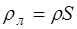 , (5.88)
, (5.88)
получим
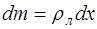 . (5.89)
. (5.89)
Для того, чтобы найти возвращающую силу, необходи-мо определить проекции на ось Y сил натяжения, дей-ствующих на рассматриваемый участок струны с обеих сторон. Проекция силы T0 в точке 1 на ось Y можно рассчитать как:
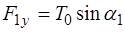 . (5.90)
. (5.90)
При малых отклонениях
 , (5.91)
, (5.91)
т.е. относительной деформации струны в точке 1 (5.54). Тог-да искомая проекция будет равна:
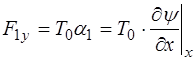 . (5.92)
. (5.92)
Проекция силы натяжения, действующей на участок струны со стороны точки 2, находится как:
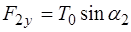 . (5.93)
. (5.93)
Угол 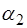 найдем при помощи разложения в ряд Тейлора (пренебрегая производными высших порядков):
найдем при помощи разложения в ряд Тейлора (пренебрегая производными высших порядков):
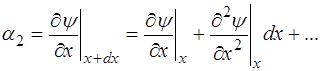 , (5.94)
, (5.94)
и получим выражение для проекции:
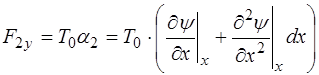 , (5.95)
, (5.95)
Поскольку с учетом (5.91) угол 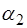 может быть найден как:
может быть найден как:
 , (5.96)
, (5.96)
то и соответствующая проекция T2x может быть записана
следующим выражением:
 . (5.97)
. (5.97)
Тогда суммарная возвращающая сила определится как:
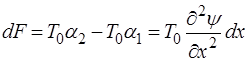 . (5.98)
. (5.98)
Запишем второй закон Ньютона для участка струны:
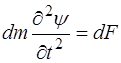 , (5.99)
, (5.99)
а с учетом (5.89) и (5.98) предыдущее выражение может быть записано как:
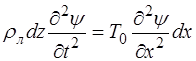 . (5.100)
. (5.100)
Освобождая производную по времени от множителей и проведя сокращение, получим уравнение:
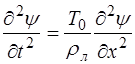 , (5.101)
, (5.101)
которое является волновым уравнением вида (5.60). Та-ким образом, возмущение распространяется в струне в виде волны со скоростью:
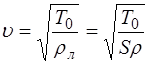 . (5.102)
. (5.102)
Решением дифференциального уравнения (5.101) явля-ется хорошо знакомая функция вида (5.63). Но это не единственное решение. Как будет показано далее, урав-нению (5.101) удовлетворяет также решение, описыва-ющее стоячую волну.
5.6.2 Скорость волны в тонком стержне и жидкости
Рассмотрим тонкий стержень, т.е. такой стержень, тол-щина которого мала по сравнению с длиной волны  . Плотность ρ материала и площадь S поперечного сечения стержня возьмем постоянными по всей дляне стержня. Расположим вдоль стержня ось X, и выделим в стержне небольшой участок длиной Δx и массой Δm (рис. 5.10). Элемент стержня
. Плотность ρ материала и площадь S поперечного сечения стержня возьмем постоянными по всей дляне стержня. Расположим вдоль стержня ось X, и выделим в стержне небольшой участок длиной Δx и массой Δm (рис. 5.10). Элемент стержня 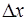 должен быть настолько малым, что-бы проекция ускорения на ось
должен быть настолько малым, что-бы проекция ускорения на ось 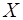 могла считаться одина-ковой для всех точек и равной
могла считаться одина-ковой для всех точек и равной 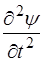 .
.
 |
Пусть вдоль оси X распространяется плоская бегущая волна. Как было показано выше, при прохождении волны левый торец выделенного участка смещается на величину 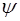 , а правый торец – на
, а правый торец – на 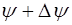 (рис. 5.11). При этом на правый левый торец действует растягивающая сила
(рис. 5.11). При этом на правый левый торец действует растягивающая сила 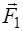 , а на левый торец – сила
, а на левый торец – сила 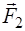 .
.
 |
Выделенный участок стержня при прохождении волны получает ускорение:
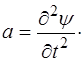 (5.103)
(5.103)
Запишем второй закон Ньютона для выделенного учас-тка стержня в проекции на ось X:
 . (5.104)
. (5.104)
Масса выделенного участка стержня определяется как:
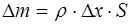 , (5.105)
, (5.105)
где  – плотность материала стержня;
– плотность материала стержня;
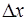 – длина выделенного участка;
– длина выделенного участка;
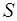 – площадь поперечного сечения стержня.
– площадь поперечного сечения стержня.
Подставим выражение для массы (5.105) в (5.104):
 . (5.106)
. (5.106)
Сила, приложенная нормально к боковым поверхнос-тям выделенного участка, создает нормальное напряже-ние 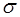 , равное:
, равное:
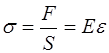 , (5.107)
, (5.107)
где E – модуль Юнга;
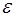 – относительная деформация, равная, согласно (5.54):
– относительная деформация, равная, согласно (5.54):
 (5.108)
(5.108)
С учетом этого, выражение (5.106) перепишем в виде:
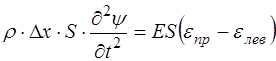 , (5.109)
, (5.109)
где 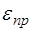 и
и 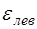 – относительная деформация правого и ле-вого торца выделенного участка стержня соответственно. Найдем выражения для
– относительная деформация правого и ле-вого торца выделенного участка стержня соответственно. Найдем выражения для 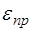 и
и 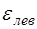 .
.
Относительная деформация в левом сечении с большой точностью может быть представлена как:
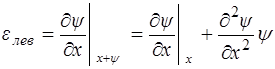 , (5.110)
, (5.110)
а в правом сечении как:
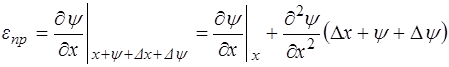 . (5.111)
. (5.111)
Подставляя полученные выражения (5.110) и (5.111) в уравнение (5.109), и сокращая на площадь поперечного сечения S, получим:
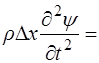
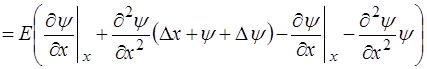 . (5.112)
. (5.112)
Раскрывая скобки и производя вычитания, получаем:
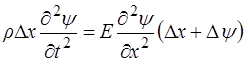 . (5.113)
. (5.113)
При распространении волн в упругой среде в основонм происходят упругие деформации, при которых относи-тельное удлинение 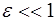 . Соответственно,
. Соответственно, 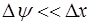 , что позволяет нам пренебречь слагаемым
, что позволяет нам пренебречь слагаемым 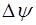 . Таким обра-зом, после сокращений получаем
. Таким обра-зом, после сокращений получаем
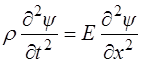 , (5.114)
, (5.114)
или
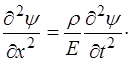 (5.115)
(5.115)
Таким образом, мы получили волновое уравнение вида (5.61). Видно, что скорость распространения упругих продольных волн в твердой среде:
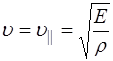 (5.116)
(5.116)
Решением уравнения (5.116) будет:
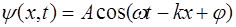 (5.117)
(5.117)
при 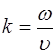 .
.
Аналогичным образом вычисляется скорость распрос-транения поперечных волн:
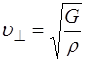 , (5.118)
, (5.118)
где G – модуль сдвига
В случае продольных волн в упругих средах под ско-ростью 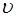 распространения волн подразумевается её зна-чение (5.116), а в случае поперечных волн – её значение (5.118).
распространения волн подразумевается её зна-чение (5.116), а в случае поперечных волн – её значение (5.118).
В формуле 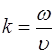 под скоростью
под скоростью 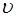 подразумевается со-ответствующая скорость распространения либо продоль-ных, либо поперечных волн.
подразумевается со-ответствующая скорость распространения либо продоль-ных, либо поперечных волн.
В дальнейшем мы при рассмотрении скорости рас-пространения волны мы индексы будем опускать.
Для вычисления скорости звука в жидкостях удобно пользоваться величиной, обратной модулю Юнга –коэф-фициентом сжатия 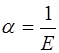 . Тогда выражение для скорос-ти звука в жидкости примет вид
. Тогда выражение для скорос-ти звука в жидкости примет вид
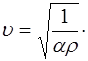 (5.119)
(5.119)
5.6.3 Скорость волны в газе
В жидкостях и газах распространяются только про-дольные волны. Мысленно вырезав канал длиной dx в на-правлении распространения плоской волны, и повторив все рассуждения, мы придем к выражению, аналогичному (5.116):
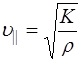 , (5.120)
, (5.120)
где K – коэффициент, аналогичный модулю Юнга E. Най-дем выражение, позволяющее определить коэффициент K.
При распространении продольных волн в среде возни-кают сжатия и растяжения отдельных слоев (рис. 5.12).
 |
Пусть возмущение дошло только до левого торца на-шего цилиндра. При этом происходит уменьшение длины 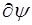 цилиндра, и, соответственно, увеличение давления dp в цилиндре. При небольших возмущениях связь избыточ-ного давления dp с относительным изменением длины цилиндрического канала
цилиндра, и, соответственно, увеличение давления dp в цилиндре. При небольших возмущениях связь избыточ-ного давления dp с относительным изменением длины цилиндрического канала 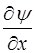 примет вид:
примет вид:
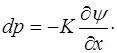 (5.121)
(5.121)
В полученном выражении (5.121) знак минус связан с тем, что приращение давления dp и длины 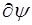 противопо-ложны по знаку. Умножив числитель и знаменатель на площадь поперечного сечения S, получим:
противопо-ложны по знаку. Умножив числитель и знаменатель на площадь поперечного сечения S, получим:
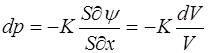 , (5.122)
, (5.122)
где 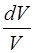 – относительное приращение объема рассматри-ваемого цилиндрического элемента среды. Таким образом, мы получили выражение для аналога модуля Юнга K:
– относительное приращение объема рассматри-ваемого цилиндрического элемента среды. Таким образом, мы получили выражение для аналога модуля Юнга K:
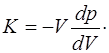 (5.123)
(5.123)
Объем  рассматриваемого элемента и его плотность
рассматриваемого элемента и его плотность  меняются при прохождении волны, но их произведение (то есть масса) остается постоянным
меняются при прохождении волны, но их произведение (то есть масса) остается постоянным 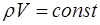 . Отсюда
. Отсюда
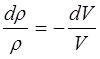 , (5.124)
, (5.124)
значит, изменение объема
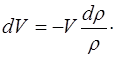 (5.125)
(5.125)
Подставив (5.125) в (5.123), получим:
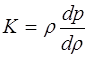 , (5.126)
, (5.126)
и, учетом этого формула (5.116) примет вид:
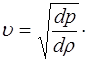 (5.127)
(5.127)
Это выражение справедливо для волн в жидкостях и газах. При распространении звука в газе сжатия и разре-жения следуют друг за другом так часто, что соседние участки среды не успевают обмениваться теплотой. Поэ-тому процесс изменения объема цилиндрического участка можно считать адиабатическим. При адиабатическом про-цессе в газе связь между давлением и объемом опреде-ляется уравнением:
 , (5.128)
, (5.128)
где 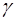 – постоянная адиабаты, равная отношению тепло-емкостей газа при постоянном давлении и объеме:
– постоянная адиабаты, равная отношению тепло-емкостей газа при постоянном давлении и объеме:
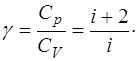 (5.129)
(5.129)
Постоянная адиабаты – величина, характерная для каждо-го газа. На основе уравнения (5.128) найдем подкоренное выражение (5.127). Продифференцируем (5.128):
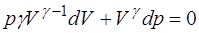 . (5.130)
. (5.130)
Разделим переменные:
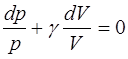 , (5.131)
, (5.131)
откуда
 , (5.132)
, (5.132)
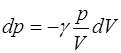 . (5.133)
. (5.133)
Из (5.125) получим:
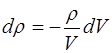 . (5.134)
. (5.134)
Подставляя (5.133) и (5.134) в (5.127), получаем следу-ющее уравнение для расчета скорости звука в газе:
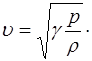 (5.135)
(5.135)
Однако эта формула неудобна для расчета. При атмос-ферном давлении и нормальной температуре газ может считаться идеальным газом, то есть таким газом, для ко-торого можно пренебречь взаимодействием между моле-кулами. Давление идеального газа можно определить из соотношения:
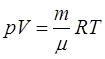 , (5.136)
, (5.136)
где 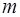 – масса газа;
– масса газа;
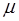 – его молярная масса;
– его молярная масса;
R – универсальная газовая постоянная;
T – абсолютная температура газа.
Плотность идеального газа определим как:
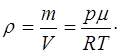 (5.137)
(5.137)
Подставив (5.136) и (5.137) в (5.135), получим уравне-ние для скорости звука в газе:
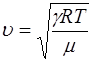 , (5.138)
, (5.138)
которое дает рассчетные данные, хорошо согласующиеся с экспериментальными.
| <== предыдущая лекция | | | следующая лекция ==> |
| The Discount Rate. Учетная ставка | | | Энергия, переносимая упругими волнами |
Дата добавления: 2015-06-12; просмотров: 1137;
