Формулы Френеля

Перпендикулярная поляризация.В этом случае вектор перпендикулярен плоскости падения и параллелен границе раздела, а плоскость поляризации ЭМВ перпендикулярна плоскости распространения.

После преобразований, подробно рассмотренных в [1], получаем формулы О. Френеля для перпендикулярно поляризованных ЭМВ:

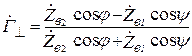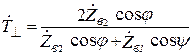; . (9.5)

Для немагнитных сред ( 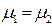) 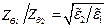(9.5) упрощается [1]:

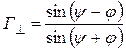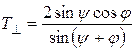; . (9.6)

Параллельная поляризация. В этом случае вектор лежит в плоскости распространения, а вектор перпендикулярен ей и параллелен границе раздела, т. е. плоскость поляризации ЭМВ параллельна плоскости ее падения.

После преобразований, подробно рассмотренных в [1–4], получаем формулы Френеля для параллельной поляризации:

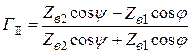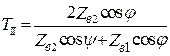; . (9.7)

Для немагнитных сред ( ) формулы (9.7) упрощаются [1]:

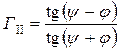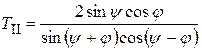; . (9.8)

Падающую ЭМВ раскладывают на две составляющие, перпендикулярную и параллельную плоскости падения, и находят составляющие отраженной и преломленной волн. Соотношения между этими составляющими ЭМП определяют характер поляризации ЭМВ. В общем случае поляризация падающей, отраженной и преломленной ЭМВ может оказаться различной.

Из выражений (9.5) и (9.7) можно получить формулы для ЭМВ, падающей на границу раздела сред нормально, положив :

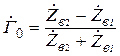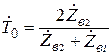; . (9.9)

Из выражения (9.9) следует, что при нормальном падении ЭМВ на границу раздела отраженная волна будет отсутствовать (Г₀ = 0) только в том случае, если волновые сопротивления сред равны (условие согласования сред).

На рис. 9.2 приведены графики зависимостей коэффициента отражения ЭМВ обеих поляризаций от угла падения при различных соотношениях между диэлектрическими проницаемостями сред [1, 3].

На рис. 9.3 приведены аналогичные графики Т(j). Следует отметить, что коэффициент преломления Т, называемый в литературе также коэффициентом прохождения во вторую среду из первой, не является энергетическимкоэффициентом прохождения. Например, при Z_в2 > Z_в1 Т будет всегда больше единицы.

Векторы Пойнтинга в разных средах связаны с разными площадями поперечных сечений лучей. Если вектор Пойнтинга наклонно падающей ЭМВ привязать к определенной площади (например, круг), то на границе раздела эта площадь изменится (круг растянется в эллипс). Во второй среде форма сохранится, но сама площадь также несколько изменится.

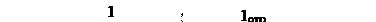Явление полного отражения.В случае, когда ЭМВ проходит из оптически более плотной среды в менее плотную ( 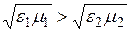), воз­ни­кает явление полного отражения (рис. 9.4).

Угол преломления y будет вещественным числом при условии:

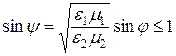. (9.10)

В этом случае вещественны также Г и Т в формулах Френеля.

Неравенство (9.10) нарушается, если угол падения j превышает некоторое значение j_кр, называемое критическим углом:

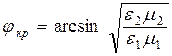. (9.11)

Если угол падения больше критического, то угол y не может быть вещественным, поскольку 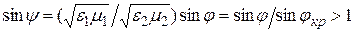. В этом случае отраженная волна уносит всю энергию, принесенную падающей.

Явление полного внутреннего отражения используется в линиях передачи нулевой связности (световоды и т. п. – см. темы 15, 18).

Явление полного прохождения.Для ЭМВ с параллельной поляризацией существует угол падения, именуемый углом Д. Брюстера 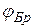, при котором отраженная волна отсутствует, а значит, ЭМВ полностью переходит во вторую среду. Для немагнитных диэлектриков ( 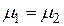) с малыми потерями, согласно выражениям (9.8), 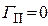при 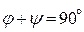, поскольку .

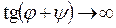По закону Снеллиуса (9.3) находим .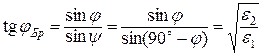

Откуда следует

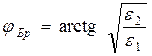. (9.12)

Для ЭМВ с перпендикулярной поляризацией аналогичного эффекта не существует, а значит, 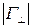всегда больше нуля.

Угол Брюстера называют также углом полной поляризации [1].

Если ЭМВ с произвольной поляризацией направлена на диэлектрическую пластину под углом 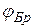, отраженный луч имеет только перпендикулярную поляризацию, так как параллельно поляризованная компонента полностью проходит через пластину.

На рис. 9.5 приведены ½Г(j)½ при различных значениях tgd второй среды при отсутствии потерь в первой.

Как видно из графиков, явление полного прохождения наблюдается только при отсутствии потерь проводимости. Если tgd > 0, то при параллельной поляризации график ½Г(j)½ будет иметь минимум, но нулевого значения не достигнет.

Если подбирать e₂ так, чтобы модуль комплексной e₂ оставался неизменным ( 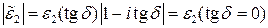), то минимум ½Г(j)½ будет достигаться при угле падения, равном углу Брюстера.

В случае перпендикулярной поляризации принципиальных изменений в поведении графиков на рис. 9.5 не происходит. Модуль Г(j) с ростом угла падения монотонно возрастает от Г₀ до единицы, а фаза Г(j) практически не отличается от 180° [1].

Диэлектрические пластины и шайбы, служащие для герметизации и крепления проводников в различных линиях связи и устройствах СВЧ, часто ставят под углом Брюстера. В этом случае на определенной частоте они полностью прозрачны для проходящих волн. Аналогичным образом поступают, если необходимо обеспечить минимальный уровень отраженной волны при падении ЭМВ из воздуха на вещество с Z_в, отличающимся от Z₀ воздуха.

Стоячая волна. КСВ. КБВ. При нормальном падении ЭМВ на границу раздела сред в первой среде складываются падающая и отраженная волны, имеющие противоположные направления распространения.

Суперпозиция ЭМВ в первой среде с учетом формул (9.6) определяется так [1]:

,

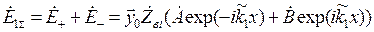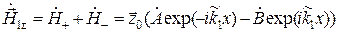. (9.13)

С учетом (9.4) выражения (9.13) преобразуем так:

,

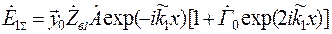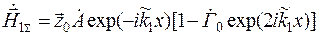. (9.14)

Выражение в квадратных скобках можно назвать множителем стоячей волны, так как эта величина показывает периодически изменяющуюся вдоль координаты х «волнистую структуру» ЭМП (рис. 9.6).

При отсутствии потерь в среде :

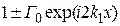. (9.15)

При монотонном изменении х второе слагаемое (9.15) вращается вокруг «1» с удвоенной (по сравнению с падающей волной) частотой. Максимальное значение составляет 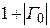, а минимальное 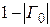. Расстояние между соседними экстремумами стоячей волны составляет p/k₁ = l₁/2 .

Если среды согласованы, то 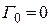, и в этом случае отраженная ЭМВ отсутствует. Если вторая среда – идеальный проводник, то 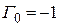, и в этом случае будет отсутствовать прошедшая ЭМВ, а в первой среде будет только стоячая волна с удвоенной (относительно падающей ЭМВ) амплитудой.

Из формул (9.13) и (9.14) получаем

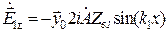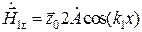, . (9.16)

На рис. 9.7 показана структура ЭМП стоячей волны. Из рис. 9.7 и выражения (9.16) сле­дует, что магнитная и электрическая составляющие имеют фазовый сдвиг на четверть длины волны (± 90°). Среднее значение вектора Пойнтинга в любой точке стоячей волны равно нулю, и передачи энергии нет.

Если перейти от комплексных амплитуд к мгновенным значениям, получим:

;

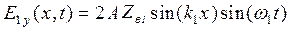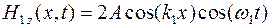. (9.17)

За период 2π/w₁ получаются распределения максимальных и минимальных значений, показанные на рис. 9.8, которые соответствуют удвоенной частоте пространственного распределения.

При экспериментальном исследовании пространственной структуры стоячей волны с помощью измерительной линии на выходе детекторной секции получится зависимость вида 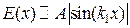(рис. 9.9).

На практике удобно оценивать неравномерность пространственного распределения ЭМП с помощью коэффициента стоячей волны (КСВ=1…¥ при 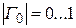) и коэффициента бегущей волны (КБВ = 1…0):

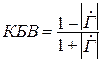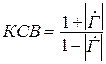; . (9.18)

На рис. 9.8 показана примерная пространственная характеристика стоячей волны на выходе детекторной секции измерительной линии. С учетом характеристики детектора получаем (КСВН (VSWR) – КСВ (SWR) по напряжению)

. (9.19)

Список рекомендуемой литературы:[1, гл. 14, с. 71–82; 2, с. 98–105; 3, гл. 13, с. 63–71; 4, с. 58–66; 5, с. 32–38; 6, с. 148–172; 7, с. 96–112; 9, с. 162–174; 10, с. 162–176; 11, с. 143–163; 12, с. 207–219; 13, с. 191–210].

Контрольные вопросы и задания

1. Сформулируйте законы Снеллиуса.

2. Являются ли законы отражения и преломления плоских волн на границе раздела сред фундаментальными законами природы?

3. Дайте определение коэффициентам отражения и прохождения. Какова область значений этих величин?

4. Каково поведение ЭМВ параллельной поляризации на границе раздела ?

5. Охарактеризуйте поведение ЭМВ перпендикулярной поляризации на границе раздела сред.

6. Укажите условие согласования сред.

7. Назовите условия полного прохождения.

8. Назовите условия полного отражения.

9. Есть ли связь между явлением полного прохождения и эффектом полной поляризации?

10. При критическом угле падения исчезает прошедшая волна. Что наблюдается, если угол падения больше критического?

11. Как изменяются условия прохождения ЭМВ через границу раздела в средах с потерями?

12. Возможно ли полное отражение ЭМВ от границы раздела диэлектриков с потерями?

13. Дайте определение стоячей волне. Объясните особенности ее ЭМП.

14. Почему стоячая ЭМВ не переносит энергию, хотя векторы ЭМП и существуют?

15. Дайте определение и укажите область значений КСВ и КБВ.

16. Можно ли получить стоячую волну из бегущих волн?

17. На границу раздела сред без потерь под углом Брюстера падает ЭМВ параллельной поляризации. Найдите соотношения между модулями векторов Пойнтинга в обеих средах и объясните полученный результат с точки зрения закона сохранения энергии.