Указания к теме. Для наклонно падающей ЭМВ на плоскую границу раздела сред необходимо научиться определять направляющие углы отраженной и прошедшей волн

Для наклонно падающей ЭМВ на плоскую границу раздела сред необходимо научиться определять направляющие углы отраженной и прошедшей волн, вычислять их амплитуды, а также коэффициенты отражения и прохождения.

Знание законов Снеллиуса и формул Френеля дает полное представление об отраженных и преломленных волнах. Для их нахождения нужно использовать граничные условия с учетом поляризации ЭМВ.

Для анализа ЭМВ на границе раздела диэлектрических сред необходимо уяснить физику явления полного прохождения и полного отражения, образование поверхностной волны и ее особенности.

Многие задачи расчета ЭМП на границе раздела диэлектрик – проводник значительно упрощаются при использовании граничных условий Леонтовича.

Следует уяснить поведение ЭМП стоячей волны; понять, почему стоячая ЭМВ не переносит энергию. Необходимо выучить определения КСВ, КБВ, коэффициентов отражения и прохождения, область определения и значений данных характеристик.

Основные сведения

ЭМ явления на границе раздела двух сред играют большую роль в теории ЭМП. Границу раздела считаем плоской и бесконечно протяженной, что позволяет рассматривать ЭМВ в виде лучей (приближение геометрической оптики).

Считаем, что оси y и z лежат в плоскости границы раздела сред (рис. 9.1), а ось x совпадает с направлением вектора нормали 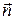для второй среды (e₂, m₂).

Наклонное падение ЭМВ. Законы Снеллиуса.Направление распространения падающей ЭМВ определяется ортом . Плоскостью падения (распространения) называют плоскость, проходящую через вектор распространения падающей ЭМВ и нормаль к поверхности раздела сред (рис. 9.1 – плоскость x0z).

Волновой вектор распространения для падающей ЭМВ имеет вид 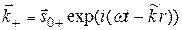. Энергия падающей ЭМВ распределяется между ЭМВ, прошедшей во вторую среду (волновой вектор ), и ЭМВ, отраженной от границы раздела сред (вектор ) .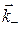

Волновые векторы падающей, отраженной и преломленной волн соответственно равны ; ; 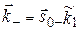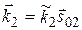[1, 2].

При заданном угле падения φ определим угол отражения φ ^– (отраженный луч) и угол преломления (прошедший луч).

Векторы ЭМП этих трех волн должны удовлетворять граничным условиям во всех точках плоскости границы раздела в любой момент времени, поэтому фазовые множители данных ЭМВ совпадают:

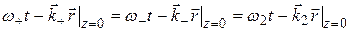. (9.1)

Из уравнения (9.1) вытекает равенство частотвсех ЭМВ 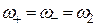. Проекци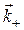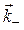и , и на ось у равны нулю. Это означает, что все волновые векторы лежат в плоскости распространения, поэтому их проекции на ось z равны:

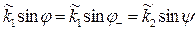, (9.2)

что позволяет сформулировать законы, открытые В. Снеллиусом [1].

1. Векторы падающей, отраженной и прошедшей ЭМВ лежат в одной плоскости (плоскости распространения).

2. Угол падения равен углу отражения ( ).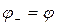

3. Отношение синусов углов падения и преломления равно отношению комплексных коэффициентов распространения во второй и первой средах (закон преломления В. Снеллиуса). Для диэлектриков с малыми потерями ( ):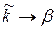

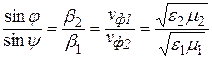, (9.3)

где 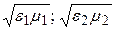– коэффициенты преломления сред.

Коэффициенты отражения и преломления.Интенсивности отраженной и преломленной волн определим через коэффициенты отражения и преломления.

Коэффициентом отраженияГ называется отношение комплексных значений напряженностей электрического поля отраженной 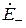и падающей 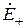волн на границе раздела (х= 0).

Коэффициентом преломленияТ во второй среде относительно первой называется аналогичное отношение преломленной 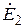и падающей волн .

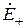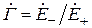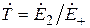; . (9.4)

Значения коэффициентов Г и Т зависят от поляризации падающей волны относительно плоскости падения.

Плоскую однородную ЭМВ, падающую на границу раздела двух сред, целесообразно разложить на перпендикулярную и параллельную поляризации.